Gambar 1. Arah vertikal $y$ sejajar dengan arah percepatan gravitasi $g$.
Mengukur sudut dalam fisika tidaklah selalu menggunakan referensi yang sama seperti dalam matematika, di mana telah terdapat istilah sudut rujukan $\theta$, yang diukur terhadap sumbu $x$ dan selalu bernilai antara $0$ dan $90$, yang merupakan sudut terkecil (acute angle) yang dibentuk oleh sisi akhir (terminal side) dan sumbu $x$ [1]. Untuk benda yang meluncur menuruni bidang miring, sudut kemiringan bidang diukur terhadap arah horisontal dan dipilih sudut terkecilnya baik untuk bidang miring licin [2] maupun dengan gesekan [3], yang hubungan sudut ini dengan sudut untuk menguraikan gaya-gaya yang bekerja pada benda kadang masih membingungkan [4]. Untuk pendulum sederhana sudut ayunan diukur terhadap arah vertikal baik untuk gerak dengan sudut simpangan kecil [5] ataupun besar [6], yang memudahkan perumusan aproksimasinya [7]. Benda yang ditarik sepanjang lantai mendatar sudut gaya diukur terhadap arah mendatar baik untuk gaya tarik [8] ataupun gaya dorong [9]. Acuan arah mendatar ini menjadi arah gerak benda bila lintasannya telah pasti seperti pada rel [10] atau arahnya merupakan informasi yang diketahui [11]. Pada gelombang sudut datang [12], sudut pantul [13], dan sudut bias [14] diukur terhadap garis normal bidang batas. Untuk gerak parabola sebuah proyektil sudut diukur terhadap arah mendatar ke sisi geraknya [15]. Dan untuk onggokan bahan butira, sudut repos (angle of repose) diukur terhadap arah mendatar dari sisi dalam bahan [16], yang dapat diukur menggunakan metode statis atau dinamis [17].
Terdapat kasus di mana sudut diukur terhadap arah vertikal dan pada kasus lain diukur pada arah horisontal.
Arah yang sejajar dengan arah suatu benda jatuh umumnya dirujuk sebagai arah vertikal atau bila dinyatakan dengan besaran fisis, arah tersebut sejajar dengan arah percepatn gravitasi $g$.

Gambar 1. Arah vertikal $y$ sejajar dengan arah percepatan gravitasi $g$.
Salah satu pemilihan arah $y$ adalah berlawanan arah dengan arah $g$, sedangkan yang lainnya adalah searah, dengan keduanya sejajar dengan arah $g$.
Pada sistem pendulum sederhana sudut simpangan diukur terhadap arah vertikal atau sumbu $y$.
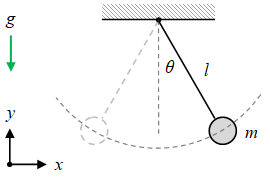
Gambar 2. Pendulum sederhana dengan sudut simpangannya $\theta$, gumpalan pendulum (pendulum bob) bermassa $m$, dan panjang tali $l$.
Dengan mengukur sudut simpangan $\theta$ terhadap arah vertikal, sebagaimana lazim dilakukan, dapat diperoleh
\begin{equation}\label{eqn:simple-pendulum-restoring-force} F_{\rm res} = -mg \sin\theta, \end{equation}
yang merupakan gaya pemulish sehingga gerak harmonis sederhana suatu pendulum sederhana dapat terjadi
Suatu kotak yang didorong atau ditarik di atas suatu permukaan mendatar oleh sebuah gaya $F_1$, yang tidak sejajar dengan permukaan mendatar, sudutnya dihitung terhadap arah mendatar atau horisontal.
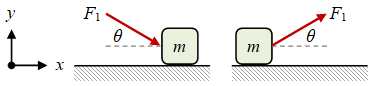
Gambar 3. Sebuah kotak didorong (kiri) atau ditarik (kanan) oleh suatu gaya $F_1$ di atas lantai mendatar.
Terlihat bahwa pemilihan arah putar dalam menentukan $\theta$ tidak dipersoalkan, asalkan diukur terhadap arah mendatar atau sumbu $x$. Dengan demikian dapat diperoleh
\begin{equation}\label{eqn:box-over-horizontal-moving-force} F_{\rm mov} = F_1 \cos\theta, \end{equation}
yang merupakan gaya yang menggerakan benda ke kanan.
Bila terdapat sebuah permukaan sudut dapat diukur dari arah normal permukaan tersebut (tegak lurus permukaan) atau dari arah sejajar permukaan.
Pada suatu permukaan dapat didefinisikan arah normal atau arah yang tegak lurus permukaan.

Gambar 4. Suatu permukaan dan vektor normalnya $\hat{n}$.
Untuk suatu permukaan yang dispesifikasikan dengan fungsi $f(x, y, z)$ maka dapat diperoleh
\begin{equation}\label{eqn:surface-normal-vector} \hat{n} = \frac{\vec{\nabla} f}{| \vec{\nabla} f |} \end{equation}
yang merupakan vektor normalnya.
Saat membahas momentum dan impuls, kasus bola yang menumbuk dinding [18], sudut datang dan sudut pantul dihitung terhadap arah normal permukaan dinding atau arah tegak lurus dinding.
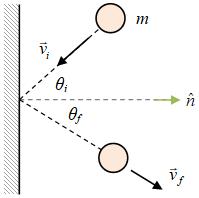
Gambar 5. Bola bermassa $m$ menumbuk dinding dengan kecepatan awal $\vec{v}_i$ dan terpantul dengan kcepatan akhir $\vec{v}_f$.
Sudut datang bola $\theta_i$ dan sudut pantulnya $\theta_f$ dihitung terhadap vektor normal permukaan $\hat{n}$, sebagaimaan disajikan dalam Gambar 5. Impuls pada bola berupa
\begin{equation}\label{eqn:ball-hitting-wall-impuls} \vec{I}_{BW} = \Delta \vec{p} = \vec{p}_f - \vec{p}_i = m\vec{v}_f - m\vec{v}_i, \end{equation}
diberikan oleh dinding. Indeks $\rm BW$ berarti pada bola oleh dinding atau on ball (B) from wall (W).
Pada kasus sebuah tangga yang bersandar pada dinding licin dan kakinya berada di atas lantai yang kasar [19], sudut diukur terhadap permukaan, baik untuk kaki tangga dengan lantai atau bagian atas tangga dengan dinding.
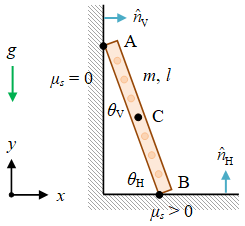
Gambar 6. Tangga bermassa $m$ dan memiliki panjang $l$ disenderkan pada dinding licin $\mu_s = 0$ dan berada di atas lantai kasar $\mu_s > 0$.
Agar tangga dalam Gambar 6 dapat berada dalam kesetimbangan statis maka perlu dipenuhi
\begin{equation}\label{eqn:leaning-ladder-sum-of-forces} \sum \vec{F} = 0 \end{equation}
sesuai dengan hukum II Newton untuk gerak translasi dan
\begin{equation}\label{eqn:leaning-ladder-sum-of-torques} \sum \tau_i = 0, \ \ \ \ i = {\rm A}, {\rm B}, {\rm C} \end{equation}
untuk gerak rotasi. Titik-titik ${\rm A}$, ${\rm B}$, ${\rm C}$ adalah tempat di mana torsi dihitung. Perhatikan bagaimana sudut kaki tangga dengan lantai $\theta _{\rm H}$ dan bagian atas tangga dengan dinding $\theta _{\rm V}$ dihitung terhadap permukaan yang bersangkutan atau sejajar dengan permukaannya.
— Sparisoma Viridi (@6unpnp) December 14, 2021