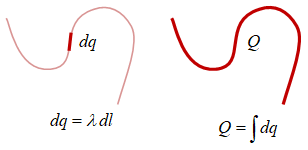
Gambar 1. Muatan garis $Q$ dengan elemen muatan $dq$ dan rapat muatan linier $\lambda$.
Unit terkecil muatan yang dapat diisolasi secara prinsip adalah muatan suatu elektron tunggal, yang amat kecil nilainya dan jarang kita berurusan langsung dengannya, sehingga lebih nyaman untuk mendeskripsikan muatan sebagai suatu kuantitas yang kontinu pada suatu daerah dalam ruang [1]. Akan tetapi perlu diingat bahwa karena muatan terkuantisasi, tidak terdapat distribusi muatan yang benar-benar kontinu [2]. Seperti halnya rapat massa, rapat muatan dapat bergantung posisi dan dalam teori elektromagnetik klasik rapat muatan diidealisasi sebagai suatu fungsi skalar kontinu dari posisi sebagaimana fluida [3]. Untuk distribusi muatan kontinu terdapat rapat muatan garis, rapat muatan luas, dan rapat muatan volume [4]. Dengan menggunakan ketiga rapat muatan ini dan bersama-sama dengan susunan muatan titik, dapat dibuat generalisasi hukum gaya Coulomb untuk keempat macam distribusi muatan (volume, permukaan, linier, dan titik) menjadi penjumlahan dari tiga integral dan satu somasi [5]. Terdapat pula keadaan khusus saat setiap muatan yang melingkupi suatu ruang dengan dimensi jauh lebih kecil dari jaraknya terhadap titik pengamatan dapat dianggap sebagai suatu titik muatan [6].
Rapat muatan linier atau garis $\lambda$ diperoleh dari
\begin{equation}\label{eqn:liniear-charge-density} \lambda = \frac{dq}{dl} \end{equation}
dengan elemen panjang $dl$ dapat berupa $dx$, $dy$, $dz$, dan $dr$ untuk muatan berbentuk garis sejajar sumbu $x$, $y$, $z$, dan berarah radial, $Rd\theta$ untuk muatan garis berbentuk cincin atau busur lingkaran dengan jari-jari $R$, dan elemen panjang lainnya yang perlu dipilih khusus seperti pada bentuk poligon ataupun heliks. Secara umum, untuk bentuk kurva sembarang, hubungan antara elemen muatan $dq$ dan muatan totalnya $Q$ adalah sebagai berikut.
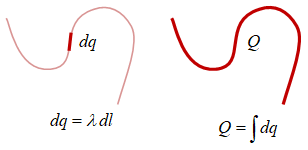
Gambar 1. Muatan garis $Q$ dengan elemen muatan $dq$ dan rapat muatan linier $\lambda$.
Total muatan suatu muatan garis diperoleh dari
\begin{equation}\label{eqn:liniear-charge-density-charge} Q = \int dq = \int \lambda dl, \end{equation}
dengan batas bawah integral merupakan permulaan integral dan batas atas integral merupakan akhir integral. Secara umum $\lambda = \lambda(l)$. Terdapat pula hubungan
\begin{equation}\label{eqn:liniear-charge-density-uniform-1} Q = \int \lambda dl = \lambda \int dl = \lambda L \end{equation}
atau
\begin{equation}\label{eqn:liniear-charge-density-uniform-2} \lambda = \frac{Q}{L}, \end{equation}
saat rapat muatan garis $\lambda$ bersifat seragam atau bernilai konstan.
Rapat muatan permukaan didapatkan dari
\begin{equation}\label{eqn:surface-charge-density} \sigma = \frac{dq}{dA} \end{equation}
dengan $dA$ adalah elemen luas yang dapat berbentuk $(dx)(dy)$, $(dy)(dz)$, $(dz)(dx)$ untuk pelat berbentuk segiempat, $(dr)(rd\theta)$ untuk pelat berbentuk cakram, cakram berongga, atau track sector [7], yang ketiganya bergantung dari batas-batas integral untuk elemen $dr$ dan $rd\theta$. Akan tetapi secara umum, untuk bentuk permukaan sembarang, hubungan antara elemen muatan $dq$ dan muatan totalnya $Q$ adalah sebagai berikut.

Gambar 2. Muatan permukaan $Q$ dengan elemen muatan $dq$ dan rapat muatan permukaan $\sigma$.
Total muatan suatu muatan permukaan diperoleh dari
\begin{equation}\label{eqn:surface-charge-density-charge} Q = \int dq = \int \sigma dA, \end{equation}
dengan batas bawah integral merupakan permulaan integral dan batas atas integral merupakan akhir integral, yang masing-masing perlu ditentukan untuk setiap elemen panjang (elemen luas merupakan perkalian dari dua elemen panjang). Secara umum, misalnya untuk sistem koordinat kartesian, $\sigma = \sigma(A) = \sigma(x, y)$. Mirip seperti pada kasus rapat muatan garis, terdapat hubungan
\begin{equation}\label{eqn:surface-charge-density-uniform-1} Q = \int \sigma dA = \sigma \int dA = \sigma A \end{equation}
atau
\begin{equation}\label{eqn:surface-charge-density-uniform-2} \sigma = \frac{Q}{A}, \end{equation}
saat rapat muatan permukaan $\sigma$ bersifat seragam atau bernilai tetap (bukan merupakan fungsi koordinat).
Rapat muatan volume dihasilkan dari
\begin{equation}\label{eqn:volume-charge-density} \rho = \frac{dq}{dV} \end{equation}
dengan $dV$ adalah elemen volume yang dapat berbentuk $(dx)(dy)(dz)$ untuk bentuk balok, $(dr)(rd\theta)(dz)$ untuk bentuk silinder, dan $(dr) (rd\theta) (r\sin\theta d\phi)$ untuk bentuk bola. Untuk bentuk volume sembarang, hubungan antara elemen muatan $dq$ dan muatan totalnya $Q$ adalah sebagai berikut.

Gambar 3. Muatan volume $Q$ dengan elemen muatan $dq$ dan rapat muatan volume $\rho$.
Selanjutnya, total muatan suatu muatan permukaan diperoleh dari
\begin{equation}\label{eqn:volume-charge-density-charge} Q = \int dq = \int \rho dV, \end{equation}
dengan batas bawah integral merupakan permulaan integral dan batas atas integral merupakan akhir integral, yang masing-masing perlu ditentukan untuk setiap elemen panjang (elemen volume merupakan perkalian dari tiga elemen panjang). Secara umum, misalnya untuk sistem koordinat kartesian, $\sigma = \sigma(V) = \sigma(x, y, z)$. Mirip seperti pada kasus rapat muatan garis dan rapat muatan permukaan, terdapat hubungan
\begin{equation}\label{eqn:volume-charge-density-uniform-1} Q = \int \rho dV = \rho \int dV = \rho V \end{equation}
atau
\begin{equation}\label{eqn:volume-charge-density-uniform-2} \rho = \frac{Q}{V}, \end{equation}
saat rapat muatan volume $\rho$ bersifat seragam atau bukan merupakan fungsi dari koordinat.

— Sparisoma Viridi (@6unpnp) December 30, 2021