
Terdapat banyak fungsi yang antiderivatifnya tidak dapat atau tidak secara mudah diekspresikan dalam bentuk tertutup, atau dengan kata lain dalam bentuk fungsi yang diketahui, sehingga ketimbang mengerjakan integral dari fungsi-fungsi tersebut secara langsung, lebih baik mencari jalan lain dengan berbagai teknis integrasi numerik untuk mencari nilai aproksimasi integralnya [1]. Dalam matematika suatu jenis aproksimasi dari suatu integral menggunakan jumlah berhingga dikenal sebagai jumlah Riemann, yang penerapan umumnya adalah untuk menghampiri luasan suatu fungsi atau garis pada grafik, dan juga panjang kurva serta hampiran lainnya, di mana jumlah tersebut dihitung dengan membuat partisi daerah menggunakan bentuk-bentuk tertentu, seperti kotak, trapesium, parabola, atau kubik [2]. Pendekatan menggunakan titik kiri kotak (LRAM), titik tengah kotak (MRAM), dan titik kanan kotak (RRAM) termasuk ke dalam metode pendekatan kotak atau rectangular approximation method [3], yang merupakan contoh formulasi yang dapat bervariasi dari suatu pendekatan. Untuk midpoint rule atau aturan titik tengah, nama lain dari midpoint rectangular approximation method, terdapat contoh kode dalam R [4]. Kemudian, selain dengan menggunakan partisi, integrasi numerik dapat pula dilakukan dengan menggunakan bilancan acak, seperti pada integrasi Monte Carlo [5].
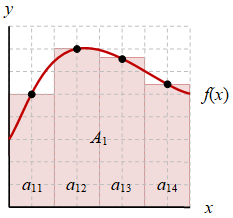
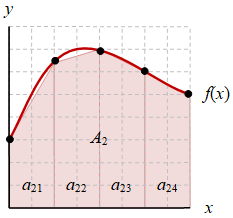
Membagi daerah di bawah kurva dalam sejumlah partisi dengan bentuk yang sama, yang mudah untuk dihitung, dan kemudian menjumlahkannya, akan memberikan hampiran dari integral tentu. Ilustrasi mengenai hal ini diberikan pada gambar berikut ini.
 |
 |
 |
Gambar 1. Luas di bawah kurva dengan integral fungsi (kiri), hampiran aturan kotak empat partisi (tengah), dan hampiran trapesium empat partisi (kanan).
Hasil integral sebenarnya adalah $A_0$ yang diberikan pda Gambar 1 (kiri) dengan dua buah hampirannya yang masing-masing menggunakan empat partisi, yaitu aturan kotak titik tengah (tengah) dan aturan trapesium (kanan). Terdapat daerah yang kosong di bawah kurva (belum terhitung) atau daerah di atas kurva (dihitung berlebih) merupakan kesalahan perhitungan integrasi numerik dibandingkan dengan hasil perhitungan analitiknya.
Dari Gambar 1 (tengah) dan (kanan) dapat dituliskan bahwa
\begin{equation}\label{eqn:sum-over-partitions} A_i = \sum_{j = 1}^N a_{ij}, \ \ \ \ i = 1, 2 \end{equation}
dengan $a_{ij}$ adalah partisi ke $j$ menggunakan hampiran $i$, $N = 4$ adalah jumlah partisi dan $i$ adalah hampiran yang digunakan, di mana $i = 1$ untuk aturan segiempat dan $i = 2$ untuk aturan trapesium. Secara umum
\begin{equation}\label{eqn:error} | A_i - A_0 | \gt 0, \ \ \ \ i = 1, 2 \end{equation}
merupakan kesalahan perhitungan numerik yang akan diperoleh.
Untuk bentuk yang lebih rumit dibandingkan dengan permasalah pada Gambar 1, misalnya menghitung luas suatu kurva tertutup, pemilihan sistem koordinat yang tepat akan memberikan hasil perhitungan yang lebih baik.
 |
 |
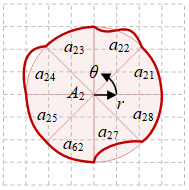 |
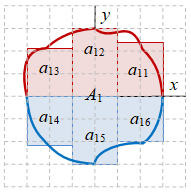
Gambar 2. Luas kurva tertutup: sebenarnya $A_0$ (kiri), dengan hampiran segiempat titik tengah $x-y$ memberikan $A_1$ (tengah), dan dengan hampiran titik tengah $r-\theta$ memberikan $A_2$ (kanan).
Terdapat bentuk yang lebih baik dinyatakan dalam koordinat polar ketimbang koordinat kartesian, dengan salah satu contohnya telah diberikan pada Gambar 2. Saat melakukan perhitungan menggunakan koordinat kartesian, kurva tertutup tersebut perlu dibagi menjadi dua bagian, yaitu bagian pertama yang berada di atas sumbu $x$ dan bagian kedua yang berada di bawah sumbu $x$, sehingga hasil luas totalnya $A_1$ merupakan penjumlahan dari dua bagian tersebut. Perhatikan bahwa masing-masing bagian masih terdiri dari tiga partisi.
Integral lipat dua atau tiga secara prinsip dapat dihitung menggunakan hampiran integrasi numerik, dengan bentuk yang paling mudah adalah dapat terpisahkan untuk masing-masing koordinat seperti
\begin{equation}\label{eqn:multiple-integral-2} \begin{array}{c} \displaystyle \int_{x_1}^{x_2} \int_{y_1}^{y_2} f(x, y) \ dy dx = \newline \displaystyle \int_{x_1}^{x_2} g(x) \ dx \int_{y_1}^{y_2} h(y) \ dy \end{array} \end{equation}
untuk integral lipat dua dan
\begin{equation}\label{eqn:multiple-integral-3} \begin{array}{c} \displaystyle \int_{x_1}^{x_2} \int_{y_1}^{y_2} \int_{z_1}^{z_2} f(x, y, z) \ dz dy dx = \newline \displaystyle \int_{x_1}^{x_2} g(x) \ dx \int_{y_1}^{y_2} h(y) \ dy \int_{z_1}^{z_2} i(z) \ dz \end{array} \end{equation}
untuk integral lipat tiga. Bila bentuk pada Persamaan \eqref{eqn:multiple-integral-2} dan \eqref{eqn:multiple-integral-3} tidak dapat dicapai perlu diterapkan pembuatan partisi dimensi yang lebih tinggi.
— Sparisoma Viridi (@6unpnp) December 19, 2021