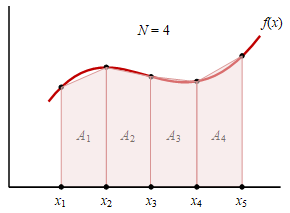
Gambar 1. Partisi pada integrasi numerik dengan aturan trapesium.
Salah satu metode integrasi numerik dengan partisi adalah aturan trapesium, yang membagi luas di bawah kurva dengan partisi-partisi berbentuk trapesium untuk menghitung suatu integral tertentu [1]. Aturan ini merupakan salah satu dari aturan-aturan terpenting dalam teori integrasi [2]. Metode ini memerlukan jumlah titik $N \ge 2$.
Suatu kurva dengan luas di bawahnya dibagi dalam partisi-partisi berbentuk trapesium diberikan pada gambar berikut ini.

Gambar 1. Partisi pada integrasi numerik dengan aturan trapesium.
Terdapat fungsi $f(x)$ yang diintegralkan mulai dari $x = x_1$ sampai dengan $x = x_5$ menggunakan empat buah partisi atau $N = 4$ sehingga terdapat luas trapesium $A_1$, .., $A_4$ seperti diberikan pada Gambar 1. Untuk satu partisi dapat dituliskan
\begin{equation}\label{eqn:trapezoidal-rule-single-partition} A_i = \left[ f(x_i) + f(x_{i+1}) \right] \frac{\Delta x}{2}, \end{equation}
dengan $\Delta x = x_{i+1} - x_i$, untuk $i = 1, .., N$. Gambar 1 memberikan ilustrasi untuk $N = 4$.
Dengan demikian untuk $N$ partisi dapat dituliskan
\begin{equation}\label{eqn:trapezoidal-rule} \int_{x_i}^{x_f} f(x) \ dx \approx \sum_{i = 1}^N \left[ f(x_i) + f(x_{i+1}) \right] \frac{\Delta x}{2}, \end{equation}
dengan
\begin{equation}\label{eqn:trapezoidal-rule-dx} \Delta x = \frac{x_f - x_i}{N}, \end{equation}
di mana $N$ jumlah partisi, $x_i$ batas bawah integral, dan $x_f$ batas atas integral.
Implementasi Persamaan \eqref{eqn:trapezoidal-rule} dan \eqref{eqn:trapezoidal-rule-dx} dalam bahasa pemrograman Python salah satunya adalah seperti berikut ini
# 0301-trapezoidal.py
# Integration with trapezoidal rule
# Sparisoma Viridi | https://github.com/dudung
# 20220223 Start this example
# define a function
fxs = "3x^2"
def f(x):
y = 3 * x * x
return y
# define integral lower and upper bounds
xbeg = 1
xend = 2
# define number of trapezoidal areas
N = 10
dx = (xend - xbeg) / N
# calculate definite integral
total = 0
x = xbeg
for i in range(N):
area = (f(x) + f(x+dx)) * dx / 2
total = total + area
x = x + dx
# display results
print("Trapezoidal rule")
print("f(x) = ", fxs)
print("xbeg = ", xbeg)
print("xend = ", xend)
print("N = ", N)
print("integral = ", total)
yang akan memberikan hasil
==== RESTART: 0301-trapezoidal.py ====
Trapezoidal rule
f(x) = 3x^2
xbeg = 1
xend = 2
N = 10
integral = 7.005000000000004
bila dijalankan. Program di atas dapat pula dijalankan secara daring di OneCompiler 3xu7ggwcf.
— Sparisoma Viridi (@6unpnp) March 9, 2022