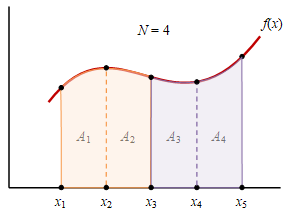
Gambar 1. Partisi pada integrasi numerik dengan aturan Simpson.
Salah satu metode integrasi numerik dengan partisi adalah aturan Simpson, yang membagi luas di bawah kurva dengan partisi-partisi berjumlah genap yang dibatasi kurva parabola dan sumbu mendatar [1]. Metode ini memerlukan jumlah titik $N \ge 2$ dan $N /2 = \lfloor N/2 \rfloor$. Dengan demikian bila digunakan jumlah partisi $N$ yang dianggap pasti bernilai genap diperoleh faktor pembagi pada lebar partisi yang berbeda [2], dibandingkan dengan memilih bahwa $N = 2M$ [1].
Suatu kurva dengan luas di bawahnya dibagi dalam setiap dua partisi yang dibatasi dengan kurva parabola dan sumbu mendatar diberikan pada gambar berikut ini.

Gambar 1. Partisi pada integrasi numerik dengan aturan Simpson.
Terdapat fungsi $f(x)$ yang diintegralkan mulai dari $x = x_1$ sampai dengan $x = x_5$ menggunakan empat buah partisi atau $N = 4$ sehingga terdapat luas trapesium $A_1$, .., $A_4$ seperti diberikan pada Gambar 1. Untuk dua partisi berurutan, yang dimulai dengan partisi berindeks ganjil, dapat dituliskan
\begin{equation}\label{eqn:simpson-rule-single-partition} A_i + A_{i+1} = \left[ f(x_i) + 4f(x_{i+1}) + f(x_{i+2}) \right] \frac{\Delta x}{3}, \end{equation}
dengan $\Delta x = x_{i+1} - x_i$, untuk $i = 1, .., N$. Gambar 1 memberikan ilustrasi untuk $N = 4$.
Dengan demikian untuk $N$ partisi dapat dituliskan
\begin{equation}\label{eqn:simpson-rule} \int_{x_i}^{x_f} f(x) \ dx \approx \sum_{i = 1}^{2M} \left[ f(x_i) + 4f(x_{i+1}) + f(x_{i+2}) \right] \frac{\Delta x}{3}, \end{equation}
dengan
\begin{equation}\label{eqn:simpson-rule-dx} \Delta x = \frac{x_f - x_i}{N}, \end{equation}
di mana $N$ jumlah partisi, $x_i$ batas bawah integral, dan $x_f$ batas atas integral. Terdapat syarat tambahan bahwa $N$ harus merupakan bilangan genap dan bernilai lebih dari atau sama dengan dua sehingga penjumlahan pada ruas kanan Persamaan \eqref{eqn:simpson-rule} dilakukan untuk $N = 2M$ suku. Cara ini lebih mudah secara komputasi untuk memformulasikan suku-sukunya ke dalam $2M$ buah partisi ketimbang dalam $N$ buah partisi.
Implementasi Persamaan \eqref{eqn:simpson-rule} dan \eqref{eqn:simpson-rule-dx} dalam bahasa pemrograman Python salah satunya adalah seperti berikut ini
# 0301-simpson.py
# Integration with simpson's rule
# Sparisoma Viridi | https://github.com/dudung
# 20220223 Start this example
# define a function
fxs = "3x^2"
def f(x):
y = 3 * x * x
return y
# define integral lower and upper bounds
xbeg = 1
xend = 2
# define number of half parabolic areas
N = 10
if (N / 2) != int(N /2):
N = N + 1
dx = (xend - xbeg) / N
M = int(N / 2)
# calculate definite integral
total = 0
x = xbeg
for i in range(M):
area = ( f(x) + 4 * f(x+dx) + f(x+2*dx) ) * dx / 3
total = total + area
x = x + 2 * dx
# display results
print("Simpson's rule")
print("f(x) = ", fxs)
print("xbeg = ", xbeg)
print("xend = ", xend)
print("N = ", N)
print("integral = ", total)
yang akan memberikan hasil
==== RESTART: 0301-simpson.py ====
Simpson's rule
f(x) = 3x^2
xbeg = 1
xend = 2
N = 10
integral = 7.0
bila dijalankan. Program di atas dapat pula dijalankan secara daring di OneCompiler 3xu7gxycg.
Perhatikan pada program yang diberikan bahwa terdapat baris
N = 10
if (N / 2) != int(N /2):
N = N + 1
dx = (xend - xbeg) / N
M = int(N / 2)
yang memaksa agar $N$ selalu bernilai genap, dengan menambahkannya dengan satu bila merupakan bilangan ganjil, yang kemudian diterapkan pada
# calculate definite integral
total = 0
x = xbeg
for i in range(M):
area = ( f(x) + 4 * f(x+dx) + f(x+2*dx) ) * dx / 3
total = total + area
x = x + 2 * dx
dengan asumsi bahwa $M = \frac12 N$ dengan $N$ bilangan genap.
— Sparisoma Viridi (@6unpnp) March 9, 2022