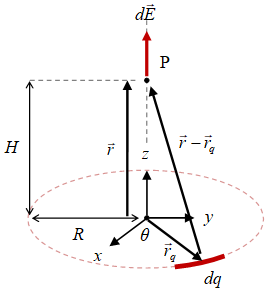
Gambar 1. Elemen muatan $dq$ pada muatan cincin dan elemen medan listrik yang disebabkannya.
Salah satu contoh lain penerapan rapat muatan linier $\lambda$ bersifat seragam adalah pada pada cincin bermuatan $Q$ dengan jari-jari $R$ untuk memperoleh medan listrik $\vec{E}$ di sepanjang sumbu cincin pada jarak $H$ dari pusat. Sebagai sumbu cincin dapat dipilih sumbu $z$ [1] atau sumbu $x$ [2]. Telah terdapat video penurunannya [3] dan juga perhitungan numeriknya menggunakan VPython [4]. Dengan mengananalogikan muatan listrik dengan massa, terdapat titik maksimum nilai medan di sepanjang sumbu cincin [5].
Medan listrik $\vec{E}_q$ pada posisi $\vec{r}$ akibat elemen muatan $dq$ yang berada pada posisi $\vec{r}_q$ diberikan oleh
\begin{equation}\label{eqn:efield-charge-distribution} d\vec{E}_q = k \ \frac{dq}{| \vec{r} - \vec{r}_q |^3} \ (\vec{r} - \vec{r}_q), \end{equation}
di mana untuk muatan garis, seperti kawat atau batang bermuatan, digunakan
\begin{equation}\label{eqn:line-charge-distribution} dq = \lambda \ dl, \end{equation}
dengan $\lambda$ adalah rapat muatan linier. Untuk saat ini dibatasi rapat muatan linier yang bersifat seragam atau bukan fungsi dari posisi $l$, yang dinyatakan dengan $\lambda \ne \lambda(l)$. Dengan demikian berlaku
\begin{equation}\label{eqn:line-charge-distribution-uniform} \lambda = \frac{Q}{L} \end{equation}
bila $L$ adalah panjang muatan garis dan $Q$ adalah muatan totalnya.
Sebuah cincin berjari-jari $R$ dan bermuatan $+Q$ terletak pada bidang $xy$ seperti diberikan pada Gambar 1. Titik amat $\rm P$ terletak pada sumbu cincin yang berhimpit dengan sumbu $y$ dan berjarak $H$ dari pusat cincin.

Gambar 1. Elemen muatan $dq$ pada muatan cincin dan elemen medan listrik yang disebabkannya.
Dari Gambar 1 dapat diperoleh
\begin{equation}\label{eqn:ring-charge-relative-position} \begin{array}{rcl} \vec{r} - \vec{r}_q & = & H \ \hat{z} - (R \cos\theta \ \hat{x} + R \sin\theta \ \hat{y}) \newline | \vec{r} - \vec{r}_q | & = & \sqrt{H^2 + R^2}, \end{array} \end{equation}
di mana telah digunakan koordinat silinder dengan
\begin{equation}\label{eqn:ring-charge-cylinder-coordinate} \begin{array}{rcl} x & = & r \cos \theta, \newline y & = & r \sin \theta, \newline r & = & x^2 + y^2. \end{array} \end{equation}
Untuk cincin elemen panjangnya adalah
\begin{equation}\label{eqn:ring-charge-length-element} dl = r \ d\theta. \end{equation}
Untuk cincin berlaku bahwa posisi radial berharga tetap $r = R$, yang akan diterapkan pada Persamaan \eqref{eqn:ring-charge-cylinder-coordinate} dan \eqref{eqn:ring-charge-length-element}. Selanjutnya adalah menggunakan Persamaan \eqref{eqn:line-charge-distribution}, \eqref{eqn:ring-charge-relative-position}, dan \eqref{eqn:ring-charge-length-element} dalam Persamaan \eqref{eqn:efield-charge-distribution} sehingga dapat diperoleh
\begin{equation}\label{eqn:dE-ring-charge} \begin{array}{rcl} d\vec{E} & = & k \displaystyle \frac{\lambda \ R d\theta}{(H^2 + R^2)^{3/2}} \ [ H \ \hat{z} - (R \cos\theta \ \hat{x} + R \sin\theta \ \hat{y}) ] \newline & = & dE_z \ \hat{z} + dE_x \ \hat{x} + dE_y \ \hat{y}. \end{array} \end{equation}
Untuk cincin penuh batas integral $\int d\theta$ memiliki batas bawah $0$ sampai $2\pi$ sehingga
\begin{equation}\label{eqn:Ex-ring-charge} \begin{array}{rcl} E_x & = & \int dE_x, \newline & = & \displaystyle -k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \int \cos\theta \ d\theta \newline & = & \displaystyle -k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \sin\theta \newline E_x ({\rm P}) & = & \displaystyle -k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \left[ \sin\theta \right]_0^{2\pi} \newline & = & 0, \end{array} \end{equation}
\begin{equation}\label{eqn:Ey-ring-charge} \begin{array}{rcl} E_y & = & \int dE_y, \newline & = & \displaystyle -k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \int \sin\theta \ d\theta \newline & = & \displaystyle k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \cos\theta \newline E_y ({\rm P}) & = & \displaystyle k \frac{\lambda \ R^2}{(H^2 + R^2)^{3/2}} \left[ \cos\theta \right]_0^{2\pi} \newline & = & 0, \end{array} \end{equation}
dan
\begin{equation}\label{eqn:Ez-ring-charge} \begin{array}{rcl} E_z & = & \int dE_z, \newline d\vec{E} & = & \displaystyle k \frac{\lambda \ RH}{(H^2 + R^2)^{3/2}} \int d\theta \newline & = & \displaystyle k \frac{\lambda \ RH}{(H^2 + R^2)^{3/2}} \ \theta \newline E_z({\rm P}) & = & \displaystyle k \frac{\lambda \ RH}{(H^2 + R^2)^{3/2}} \left[ \theta \right]_0^{2\pi} \newline & = & \displaystyle k \frac{\lambda \ RH}{(H^2 + R^2)^{3/2}} (2\pi - 0) \newline & = & \displaystyle k \frac{\lambda \ 2\pi R \ H}{(H^2 + R^2)^{3/2}} \newline & = & \displaystyle k \frac{Q \ H}{(H^2 + R^2)^{3/2}} \end{array} \end{equation}
Untuk muatan cincin utuh $L = 2\pi L$ sehingga untuk rapat muatan linier seragam diperoleh $Q = 2\pi L \lambda$ seperti diberikan oleh Persamaan \eqref{eqn:line-charge-distribution-uniform}, sebagaimana diterapkan pada baris terakhir Persamaan \eqref{eqn:Ey-ring-charge}. Dengan demikian diperoleh
\begin{equation}\label{eqn:E-ring-charge-axis-solution} \vec{E}({\rm P}) = \hat{z} k \frac{Q \ H}{(H^2 + R^2)^{3/2}}, \end{equation}
yang merupakan medan listrik sepanjang sumbu $z$ atau sumbu cincin untuk sistem yang diberikan pada Gambar 1.
Bila medan listrik di sepanjang sumbu cincin diamati untuk jarak yang jauh atau tepatnya $H > > R$ maka solusi yang diberikan oleh Persamaan \eqref{eqn:E-ring-charge-axis-solution} akan menjadi
\begin{equation}\label{eqn:E-ring-charge-axis-solution-long-distance} \begin{array}{rcl} \vec{E}({\rm P}) & = & \displaystyle \hat{z} k \frac{Q \ H}{(H^2 + R^2)^{3/2}} \newline & = & \displaystyle \hat{z} k \frac{Q}{H^{-1}(H^2 + R^2)^{3/2}} \newline & = & \displaystyle \hat{z} k \frac{Q}{H^{-1}H^3[1 + (R/H)^2]^{3/2}} \newline & \approx & \displaystyle \hat{z} k \frac{Q}{H^2}, \end{array} \end{equation}
dengan bentuknya seperti medan listrik yang disebabkan oleh muatan titik. Pendekatan berikut
\begin{equation}\label{eqn:E-ring-charge-axis-solution-long-distance-approximation} 1 + (R/H)^2 \approx 1 \end{equation}
telah digunakan untuk mendapatkan baris terakhir dari Persamaan \eqref{eqn:E-ring-charge-axis-solution-long-distance}.
Medan listrik untuk cincin tidak penuh, atau lebih tepatnya berupa busur lingkaran, tidak dapat diperoleh dari Persamaan \eqref{eqn:E-ring-charge-axis-solution} akan tetapi harus menggunakan Persamaan \eqref{eqn:Ex-ring-charge}, \eqref{eqn:Ey-ring-charge}, dan \eqref{eqn:Ez-ring-charge}. Hal ini tidak akan dibahas di sini.
— Sparisoma Viridi (@6unpnp) January 10, 2022
electric charge • electric field • charge distribution