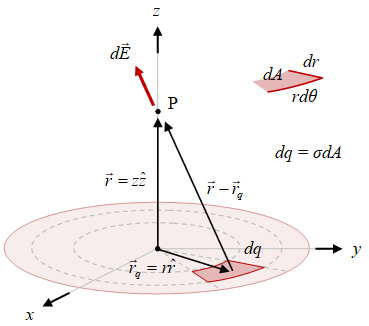
Gambar 1. Elemen muatan $dq$ dari sebuah muatan permukaan berbentuk cakram dan elemen medan listrik $d\vec{E}$ yang disebabkannya.
Saat membahas medan listrik yang disebabkan oleh muatan permukaan berbentuk sebuah cakram atau pelat bundar pada sumbu cakram, umumnya digunakan pendekatan elemen muatan berbentuk cincin [1, 2, 3], yang telah menghilangkan komponen-komponen medan listrik selain komponen yang sejajar sumbu. Hal ini akan membuat bentuk-bentuk seperti sektor lingkaran [4] dan segmen anulus [5] tidak dapat digunakan sebagai bentuk muatan permukaan untuk dihitung medan listrik yang disebabkannya. Dengan menggunakan elemen luas lingkaran, sebagai cara terakhir dari tiga cara mengitung luas lingkaran [6], hasil yang lebih umum dapat diperoleh.
Suatu distribusi muatan dengan elemen muatan $dq$ yang terletak pada posisi $\vec{r}_q$ memberikan elemen medan listrik $d\vec{E}$ pada posisi $\vec{r}$ mengikuti
\begin{equation}\label{eqn:electric-field-charge-distribution} d\vec{E}_q = k \ \frac{dq}{| \vec{r} - \vec{r}_q |^3} \ (\vec{r} - \vec{r}_q), \end{equation}
dengan $k = 8.9875517923(14)\times 10^9$ ${\rm kg \cdot m^3 \cdot s^{-2} \cdot C^{-2}}$ adalah konstanta Coulomb.
Rapat muatan permukaan diberikan oleh
\begin{equation}\label{eqn:surface-charge-density} \sigma = \frac{dq}{dA}, \end{equation}
yang untuk distribusi muatan seragam akan menjadi
\begin{equation}\label{eqn:surface-charge-density-uniform} \sigma = \frac{Q}{A}, \end{equation}
dengan $A$ adalah luas permukaan dan $Q$ muatan totalnya. Untuk sistem berbentuk cakram
\begin{equation}\label{eqn:area-element} dA = (dr)(rd\theta) \end{equation}
merupakan elemen luasnya dalam koordinat polar dan sillinder. Dan
\begin{equation}\label{eqn:radial-unit-vector} \hat{r} = \hat{x} \cos\theta + \hat{y} \sin\theta \end{equation}
merupakan vektor satuan arah radialnya.
Sebuah muatan permukaan berbentuk cakram dengan dengan jari-jari $R$ dan muatan total $Q$ memiliki elemen muatan $dq$ yang memberikan elemen medan listrik $d\vec{E}$ pada titik amat $\rm P$ yang terletak sepanjang sumbu $z$ pada jarak $z$ dari cakram. Ilustrasi sistem ini diberikan pada Gambar 1.

Gambar 1. Elemen muatan $dq$ dari sebuah muatan permukaan berbentuk cakram dan elemen medan listrik $d\vec{E}$ yang disebabkannya.
Dari Gambar 1 dapat diperoleh
\begin{equation}\label{eqn:uniformly-charged-disc-relative-position} \begin{array}{rcl} \vec{r} - \vec{r}_q & = & z\hat{z} - r\hat{r}, \newline |\vec{r} - \vec{r}_q| & = & \sqrt{z^2 + r^2}. \end{array} \end{equation}
Substitusi Persamaan \eqref{eqn:surface-charge-density}, \eqref{eqn:area-element}, \eqref{eqn:radial-unit-vector}, dan \eqref{eqn:uniformly-charged-disc-relative-position} ke Persamaan \eqref{eqn:electric-field-charge-distribution} akan memberikan
\begin{equation}\label{eqn:uniformly-charged-disc-electric-field} \begin{array}{rcl} d\vec{E}_q & = & \displaystyle k \ \frac{\sigma \ dA}{(z^2 + r^2)^{3/2}} \ (z\hat{z} - r\hat{r}) \newline & = & \displaystyle k \ \frac{\sigma \ (dr \ rd\theta)}{(z^2 + r^2)^{3/2}} \ [z\hat{z} - r(\hat{x} \cos\theta + \hat{y} \sin\theta)] \newline & = & \hat{z} dE_z + \hat{x} dE_x + \hat{y} dE_y, \newline \vec{E}_q & = & \hat{z} E_z + \hat{x} E_x + \hat{y} E_y, \end{array} \end{equation}
dengan
\begin{equation}\label{eqn:uniformly-charged-disc-electric-field-Ex} E_x = -k\sigma \int \frac{r^2 dr}{(z^2 + r^2)^{3/2}} \int \cos\theta d\theta \end{equation}
\begin{equation}\label{eqn:uniformly-charged-disc-electric-field-Ey} E_y = -k\sigma \int \frac{r^2 dr}{(z^2 + r^2)^{3/2}} \int \sin\theta d\theta \end{equation}
dan
\begin{equation}\label{eqn:uniformly-charged-disc-electric-field-Ez} E_z = k \sigma z \int \frac{rdr}{(z^2 + r^2)^{3/2}} \int d\theta. \end{equation}
Dengan
\begin{equation}\label{eqn:int-05f} \begin{array}{rcl} \displaystyle \int \frac{r^2 dr}{(z^2 + r^2)^{3/2}} & = & \displaystyle - \frac{r}{\sqrt{z^2 + r^2}} \newline && \displaystyle + \ln \left| \frac{\sqrt{z^2 + r^2}}{z} + \frac{r}{z} \right| + C \end{array} \end{equation}
dan
\begin{equation}\label{eqn:int-00} \int \frac{r \ dr}{(z^2 + r^2)^{3/2}} = - \frac{1}{(z^2 + r^2)^{1/2}} + C, \end{equation}
Persamaan \eqref{eqn:uniformly-charged-disc-electric-field-Ex}, \eqref{eqn:uniformly-charged-disc-electric-field-Ey}, dan \eqref{eqn:uniformly-charged-disc-electric-field-Ez} dapat dipecahkan.
Untuk $R$ batas bawah integralnya adalah $R_1$ dan batas atasnya adalah $R_2$, sedangkan untuk $\theta$ batas bawah integralnya adalah $\theta_1$ dan baas atasnya adalah $\theta_2$.
Untuk arah $x$ dapat diperoleh
\begin{equation}\label{eqn:Ex-solution} \begin{array}{rcl} E_x({\rm P}) & = & \displaystyle -k\sigma (\sin\theta_2 - \sin\theta_1) \ \cdot \newline && \displaystyle \left( - \frac{R_2}{\sqrt{z^2 + R_2^2}} + \ln \left| \frac{\sqrt{z^2 + R_2^2}}{z} + \frac{R_1}{z} \right| \right. \newline && \displaystyle \left. + \frac{R_1}{\sqrt{z^2 + R_1^2}} - \ln \left| \frac{\sqrt{z^2 + R_1^2}}{z} + \frac{R_1}{z} \right| \right). \end{array} \end{equation}
Untuk arah $y$ dapat diperoleh
\begin{equation}\label{eqn:Ey-solution} \begin{array}{rcl} E_y({\rm P}) & = & \displaystyle k\sigma (\cos\theta_2 - \cos\theta_1) \ \cdot \newline && \displaystyle \left( - \frac{R_2}{\sqrt{z^2 + R_2^2}} + \ln \left| \frac{\sqrt{z^2 + R_2^2}}{z} + \frac{R_1}{z} \right| \right. \newline && \displaystyle \left. + \frac{R_1}{\sqrt{z^2 + R_1^2}} - \ln \left| \frac{\sqrt{z^2 + R_1^2}}{z} + \frac{R_1}{z} \right| \right). \end{array} \end{equation}
Untuk arah $z$ dapat diperoleh
\begin{equation}\label{eqn:Ez-solution} E_z({\rm P}) = -k \sigma z (\theta_2 - \theta_1) \left( \frac{1}{\sqrt{z^2 + R_2^2}} - \frac{1}{\sqrt{z^2 + R_1^2}} \right). \end{equation}
Keseluruhan medan listrik pada titik amat $\rm P$ diperoleh dengan menjumlahan secara vektor Persamaan \eqref{eqn:Ex-solution}, \eqref{eqn:Ey-solution}, dan \eqref{eqn:Ez-solution}
\begin{equation}\label{eqn:E-solution} \vec{E}({\rm P}) = \hat{x} E_x({\rm P}) + \hat{y} E_y({\rm P}) + \hat{z} E_z({\rm P}). \end{equation}
Persamaan \eqref{eqn:E-solution} ini dapat diterapkan untuk cakram, anulus, sektor lingkaran, dan segmen anulus.
Untuk bentuk muatan permukaan berbentuk sirkular terdapat cakram dan anulus.
Untuk anulus perlu diterapkan $\theta_1 = 0$ dan $\theta_2 = 2\pi$ pada Persamaan \eqref{eqn:Ex-solution}, \eqref{eqn:Ey-solution}, dan \eqref{eqn:Ez-solution}, yang akan menghasilkan
\begin{equation}\label{eqn:E-solution-annulus} \vec{E}({\rm P}) = \hat{z} k \sigma 2\pi \left( \frac{z}{\sqrt{z^2 + R_1^2}}- \frac{z}{\sqrt{z^2 + R_2^2}} \right). \end{equation}
sebagai hasilnya. Urutan suku dalam kurung telah diubah mengingat $R_1 < R_2$.
Untuk cakram perlu diterapkan $R_1 = 0$, $R_2 = R$, $\theta_1 = 0$, dan $\theta_2 = 2\pi$ pada Persamaan \eqref{eqn:Ex-solution}, \eqref{eqn:Ey-solution}, dan \eqref{eqn:Ez-solution}, yang akan memberikan
\begin{equation}\label{eqn:E-solution-disc} \vec{E}({\rm P}) = \hat{z} k \sigma 2\pi \left( \frac{z}{|z|}- \frac{z}{\sqrt{z^2 + R^2}} \right). \end{equation}
sebagai hasilnya. Perhatikan bahwa suku di dalam kurung telah diubah urutannya.
Baik untuk anulus maupun cakram, komponen pada arah $x$ dan $y$, pada masing-masing komponen terdapat suku $(\sin\theta_2 - \sin\theta_1)$ dan $(\cos\theta_2 - \cos\theta_1)$, berturut-turut, yang akan menjadi bernilai nol saat diterapkan $\theta_1 = 0$ dan $\theta_2 = 2\pi$.
Untuk cakram yang amat luas atau $R = \infty$ Persamaan \eqref{eqn:E-solution-disc} akan menjadi
\begin{equation}\label{eqn:E-solution-disc-very-large} \vec{E}({\rm P}) = \hat{z} k \sigma 2\pi \frac{z}{|z|} = \hat{z} \frac{\sigma}{2\epsilon_0} \frac{z}{|z|}, \end{equation}
yang besarnya cukup dituliskan dalam bentuk
\begin{equation}\label{eqn:E-solution-disc-very-large-magnitude} E_{\rm large \ disc} = \frac{\sigma}{2\epsilon_0}, \end{equation}
karena suku $\hat{z} \cdot (z/|z|)$ hanya menunjukkan arah medan listriknya. Persamaan \eqref{eqn:E-solution-disc-very-large} atau \eqref{eqn:E-solution-disc-very-large-magnitude} akan digunakan dalam menentukan medan listrik oleh pelat luas, yang juga dimanfaatkan dalam kapasitor.
— Sparisoma Viridi (@6unpnp) January 10, 2022
electric charge • electric field • charge distribution