
Gambar 1. Elemen medan listrik $d\vec{E}$ disebabkan oleh elemen muatan $dq$ yang merupakan bagian dari muatan garis dengan panjang total $L_1 + L_2$.
Untuk mendapatkan medan listrik akibat muatan garis diperlukan rapat muatan linier yang disimbolkan dengan $\lambda$ [1] dan kadang juga dengan $\mu$ [2]. Medan listrik di sekitar kawat lurus dapat dihitung pada posisi tengah-tengah panjang kawat sehingga dapat memanfaatkan simetri untuk memudahkan perhitungan [3] atau menghitungnya pada sembarang posisi di sekitar kawat lurus sehingga memberikan hasil yang lebih umum [4]. Salah satu kasus yang menarik adalah bila panjang kawat dapat dianggap tak-hingga atau jauh lebih besar dari jarak titik yang ingin diobservasi terhadap kawat [5]. Terdapat pula kasus di mana medan listrik dihitung pada jarak tertentu dari salah satu ujung kawat lurus, yang kadang dapat cukup membingungkan [6].
Medan listrik yang disebabkan oleh distribusi muatan yang terdapat pada posisi $\vec{r}_q$ akan menyebabkan elemen medan listrik $d\vec{E}$ pada posisi $\vec{r}$ dalam bentuk
\begin{equation}\label{eqn:efield-charge-distribution} d\vec{E}_q = k \ \frac{dq}{| \vec{r} - \vec{r}_q |^3} \ (\vec{r} - \vec{r}_q), \end{equation}
dengan
\begin{equation}\label{eqn:coulomb-constant} \begin{array}{rcl} k & = & \displaystyle \frac{1}{4\pi\epsilon_0} \newline & = & 8.9875517923(14)\times 10^9 \newline && {\rm kg \cdot m^3 \cdot s^{-2} \cdot C^{-2}} \end{array} \end{equation}
adalah konstanta Coulomb, yang untuk praktisnya diingat dengan nilai $9\times10^9$ sebagaimana diajarkan di universitas [7]. Untuk muatan garis elemen muatan $dq$ pada Persamaan \eqref{eqn:efield-charge-distribution} digantikan oleh
\begin{equation}\label{eqn:charge-element} dq = \lambda dl \end{equation}
dengan $\lambda$ adalah rapat muatan linier dan $dl$ adalah elemen panjang yang dapat berupa $dx$, $dy$, atau $dz$ dalam koordinat kartesian. Secara umum $\lambda = \lambda(l)$, sedangkan untuk kasus rapat muatan seragam $\lambda \ne \lambda(l)$ atau bernilai konstan. Pembahasan saat ini dibatasi untuk kasus $\lambda \ne \lambda(l)$.
Terdapat suatu muatan garis berbentuk kawat bermuatan total $Q$ yang terletak pada sumbu $x$ dengan membentang dari $x = -L_1$ sampai $x = +L_2$ seperti ditunjukkan pada Gambar 1. Titik pengamatan $\rm P$ tempat medan listrik ingin dihitung berjarak tegak lurus $R$ dari kawat dan terletak pada sumbu $y$.

Gambar 1. Elemen medan listrik $d\vec{E}$ disebabkan oleh elemen muatan $dq$ yang merupakan bagian dari muatan garis dengan panjang total $L_1 + L_2$.
Dari Gambar 1 dapat diperoleh
\begin{equation}\label{eqn:perp-dist-case-rel-dist} \begin{array}{rcl} \vec{r} - \vec{r}_q & = & R\hat{y} - x\hat{x}, \newline |\vec{r} - \vec{r}_q| & = & \sqrt{R^2 + x^2}. \end{array} \end{equation}
Substitusi Persamaan \eqref{eqn:charge-element}, dengan $dl \equiv dx$, dan \eqref{eqn:perp-dist-case-rel-dist} ke Persamaan \eqref{eqn:efield-charge-distribution} akan menghasilkan
\begin{equation}\label{eqn:dE-line-charge-perp} \begin{array}{rcl} d\vec{E}_q & = & \displaystyle k \ \frac{dq}{| \vec{r} - \vec{r}_q |^3} \ (\vec{r} - \vec{r}_q) \newline & = & \displaystyle k \ \frac{\lambda dx}{(R^2 + x^2)^{3/2}} \ (R\hat{y} - x\hat{x}) \newline & = & dE _{qx} \ \hat{x} + dE _{qy} \ \hat{y} \newline \vec{E}_q & = & E _{qx} \ \hat{x} + E _{qy} \ \hat{y} \end{array} \end{equation}
dengan
\begin{equation}\label{eqn:dEx-line-charge-perp} E _{qx} = \int dE _{qx} = -k\lambda \int \frac{x \ dx}{(R^2 + x^2)^{3/2}} \end{equation}
dan
\begin{equation}\label{eqn:dEy-line-charge-perp} E _{qy} = \int dE _{qy} = kR\lambda \int \frac{dx}{(R^2 + x^2)^{3/2}}. \end{equation}
Bagian integral pada suku paling kanan di kedua Persamaan \eqref{eqn:dEx-line-charge-perp} dan \eqref{eqn:dEy-line-charge-perp} perlu dipecahkan untuk mendapatkan medan listrik di titik $\rm P$.
Untuk arah $x$ diperoleh
\begin{equation}\label{eqn:dEx-line-charge-perp-result} \begin{array}{rcl} E _{qx} & = & \displaystyle -k\lambda \int \frac{x \ dx}{(R^2 + x^2)^{3/2}} \newline & = & \displaystyle (-k\lambda) \left(-\frac{1}{(R^2 + x^2)^{1/2}} \right) + C \newline & = & \displaystyle \frac{k\lambda}{(R^2 + x^2)^{1/2}} + C \end{array} \end{equation}
dan untuk aray $y$ didapatkan
\begin{equation}\label{eqn:dEy-line-charge-perp-result} \begin{array}{rcl} E _{qy} & = & \displaystyle kR\lambda \int \frac{dx}{(R^2 + x^2)^{3/2}} \newline & = & \displaystyle (kR\lambda) \left( \frac{1}{R^2} \ \frac{x}{\sqrt{R^2 + x^2}} \right) + C \newline & = & \displaystyle \frac{k\lambda}{R} \ \frac{x}{\sqrt{R^2 + x^2}} + C. \end{array} \end{equation}
Persamaan \eqref{eqn:dEx-line-charge-perp-result} dan \eqref{eqn:dEy-line-charge-perp-result} masih merupakan hasil integral tak-tentu. Untuk mendapatkan nilai medan listrik pada arah $x$ dan $y$ pada titik $\rm P$ seperti dalam Gambar 1 perlu dimasukkan batas-batas integral yang diberikan pada Gambar 2 berikut ini.

Gambar 2. Batas-batas integral untuk mencari medan listrik di titik $\rm P$, yang dapat berupa $x$ atau $\theta$ bergantung pada bentuk akhir antiderivatif yang diperoleh apakah dalam fungsi $x$ atau $\theta$.
Dengan memanfaatkan informasi yang diberikan dalam Gambar 2 Persamaan \eqref{eqn:dEx-line-charge-perp-result} dan \eqref{eqn:dEy-line-charge-perp-result} akan menjadi
\begin{equation}\label{eqn:dEx-line-charge-perp-result-at-P} \begin{array}{rcl} E _{qx}({\rm P}) & = & \displaystyle -k\lambda \int _{-L_1}^{L_2} \frac{x \ dx}{(R^2 + x^2)^{3/2}} \newline & = & \displaystyle k\lambda \left[ \frac{1}{\sqrt{R^2 + x^2}} \right] _{x = -L_1}^{L_2} \newline & = & \displaystyle k\lambda \left( \frac{1}{\sqrt{R^2 + (L_2)^2}} - \frac{1}{\sqrt{R^2 + (-L_1)^2}} \right) \newline & = & \displaystyle k\lambda \left( \frac{1}{\sqrt{R^2 + L_2^2}} - \frac{1}{\sqrt{R^2 + L_1^2}} \right) \end{array} \end{equation}
dan
\begin{equation}\label{eqn:dEy-line-charge-perp-result-at-P} \begin{array}{rcl} E _{qy}({\rm P}) & = & \displaystyle kR\lambda \int _{-L_1}^{L_2} \frac{dx}{(R^2 + x^2)^{3/2}} \newline & = & \displaystyle \frac{k\lambda}{R} \left[ \frac{x}{\sqrt{R^2 + x^2}} \right] _{x = -L_1}^{L_2} \newline & = & \displaystyle \frac{k\lambda}{R} \left[ \frac{(L_2)}{\sqrt{R^2 + (L_2)^2}} - \frac{(-L_1)}{\sqrt{R^2 + (-L_1)^2}} \right] \newline & = & \displaystyle \frac{k\lambda}{R} \left( \frac{L_2}{\sqrt{R^2 + L_2^2}} + \frac{L_1}{\sqrt{R^2 + L_1^2}} \right). \end{array} \end{equation}
Dengan demikian dapat dituliskan
\begin{equation}\label{eqn:E-line-charge-perp-solution} \begin{array}{rcl} \vec{E}_q({\rm P}) & = & E _{qx} \ \hat{x} + dE _{qy} \ \hat{y} \newline & = & \displaystyle k\lambda \left( \frac{1}{\sqrt{R^2 + L_2^2}} - \frac{1}{\sqrt{R^2 + L_1^2}} \right) \ \hat{x} \newline && + \displaystyle \frac{k\lambda}{R} \left( \frac{L_2}{\sqrt{R^2 + L_2^2}} + \frac{L_1}{\sqrt{R^2 + L_1^2}} \right) \ \hat{y}, \end{array} \end{equation}
yang merupakan solusi dari medan listrik di titik $\rm P$ pada Gambar 1.
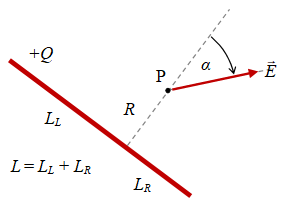
Gambar 3. Sebuah kawat muatan garis dengan panjang $L = L_L + L_R$ berorientasi sembarang deengan medan listrik $\vec{E}$ di titik $\rm P$ yang disebabkannya, di mana total muatannya adalah $+Q$ dan rapat muatan liniernya bersifat seragam $\lambda \ne \lambda(l)$.
Persamaan \eqref{eqn:E-line-charge-perp-solution} dapat dibuat menjadi lebih umum sehingga dapat menggambarkan medan listrik pada titik $\rm P$ pada Gambar 3 yang memiliki orientasi sembarang.
Persamaan \eqref{eqn:E-line-charge-perp-solution} merupakan solusi dari Gambar 4 di bawah ini.
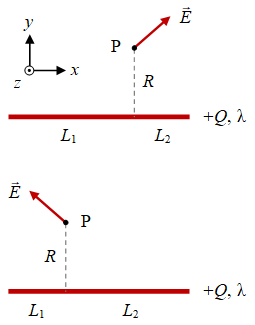
Gambar 4. Medan listrik oleh suatu muatan garis berbentuk kawat berhingga dengan panjang sebelah kiri $L_1$ dan sebelah kanan $L_2$ dari titik pengamatan $\rm P$ yang berjarak $R$ dari kawat.
Perbedaan panjang $L_1$ dan $L_2$ akan menentukan arah medan listrik yang diperoleh dari
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-1} \begin{array}{rcl} \vec{E}_q({\rm P}) & = & \displaystyle k\lambda \left( \frac{1}{\sqrt{R^2 + L_2^2}} - \frac{1}{\sqrt{R^2 + L_1^2}} \right) \ \hat{x} \newline && + \displaystyle \frac{k\lambda}{R} \left( \frac{L_2}{\sqrt{R^2 + L_2^2}} + \frac{L_1}{\sqrt{R^2 + L_1^2}} \right) \ \hat{y}, \end{array} \end{equation}
yang merupakan penulisan kembali dari Persamaan \eqref{eqn:E-line-charge-perp-solution}. Perhatikan bahwa komponen pada arah $y$ selalu positif, sedangkan komponen pada arah $x$ ditentukan oleh nilai $L_1$ dan $L_2$. Bila $L_1 > L_2$ maka $E_x > 0$ dan bila $L_1 < L_2$ maka $E_x < 0$. Selanjutnya
Terdapat kasus titik $\rm P$ terletak di tengah-tengah kawat atau $L_1 = L_2$ sebagaimana disajikan pada Gambar 5.

Gambar 5. Medan listrik oleh suatu muatan garis berbentuk kawat berhingga dengan panjang sebelah kiri $L_1$ dan sebelah kanan $L_2$ dari titik pengamatan $\rm P$ yang berjarak $R$ dari kawat, untuk kasus $L_1 = L_2$.
Kasus pada Gambar 5 akan membuat Persamaan \eqref{eqn:E-line-charge-perp-solution} menjadi
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-2} \begin{array}{rcl} \vec{E}_q({\rm P}) & = & \displaystyle \frac{k\lambda}{R} \left( \frac{L_2}{\sqrt{R^2 + L_2^2}} + \frac{L_1}{\sqrt{R^2 + L_1^2}} \right) \ \hat{y}, \end{array} \end{equation}
yang tidak lagi memiliki komponen pada arah $x$ karena kontribusi dari bagian dengan panjang $L_1$ di sebelah kiri saling meniadakan dengan kontribusi dari bagian dengan panjang $L_2$ di sebelah kanan.
Persamaan \eqref{eqn:E-line-charge-perp-solution} dapat pula digunakan untuk jarak tegak lurus terhadap muatan garis di sisi salah satu ujung kawat yang diberikan ilustrasinya pada Gambar 6 di bawah ini,
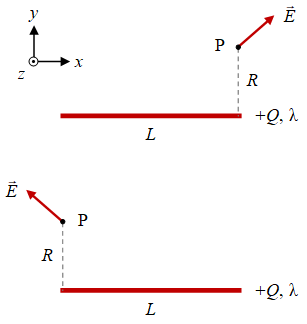
Gambar 6. Medan listrik oleh suatu muatan garis berbentuk kawat berhingga dengan panjang sebelah kiri $L_1$ dan sebelah kanan $L_2$ dari titik pengamatan $\rm P$ yang berjarak $R$ dari kawat, untuk kasus $L_1 = L$, $L_2 = 0$ (atas) dan $L_1 = 0$, $L_2 = L$ (bawah).
Solusi dari kedua kasus pada Gambar 6 untuk $L_1 = L$, $L_2 = 0$ adalah
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-3-L2=0} \begin{array}{rcl} \vec{E}_q({\rm P}) & = & \displaystyle k\lambda \left( \frac{1}{R} - \frac{1}{\sqrt{R^2 + L^2}} \right) \ \hat{x} \newline && + \displaystyle \frac{k\lambda}{R} \left( \frac{L}{\sqrt{R^2 + L^2}} \right) \ \hat{y} \end{array} \end{equation}
dan untuk $L_1 = 0$, $L_2 = L$ adalah
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-3-L1=0} \begin{array}{rcl} \vec{E}_q({\rm P}) & = & \displaystyle k\lambda \left( \frac{1}{\sqrt{R^2 + L^2}} - \frac{1}{R} \right) \ \hat{x} \newline && + \displaystyle \frac{k\lambda}{R} \left( \frac{L}{\sqrt{R^2 + L^2}} \right) \ \hat{y}. \end{array} \end{equation}
Perhatikan bahwa komponen medan listrik pada arah $y$ adalah sama dan pada arah $x$ berbeda tanda pada Persamaan \eqref{eqn:E-line-charge-perp-solution-case-3-L2=0} dan \eqref{eqn:E-line-charge-perp-solution-case-3-L1=0}.
Selanjutnya bila kawat dapat dianggap amat panjang dan ingin dicari medan listrik pada jarak tegak lurus di sisi salah satu ujungnya seperti diberikan pada Gambar 7.

Gambar 7. Medan listrik oleh suatu muatan garis berbentuk kawat tak-berhingga dengan panjang sebelah kiri $L_1$ dan sebelah kanan $L_2$ dari titik pengamatan $\rm P$ yang berjarak $R$ dari kawat, untuk kasus $L_1 = \infty$, $L_2 = 0$ (atas) dan $L_1 = 0$, $L_2 = \infty$ (bawah).
Solusi dari Gambar 7 dapat diperoleh kembali dari Persamaan \eqref{eqn:E-line-charge-perp-solution} atau lebih cepat dari Persamaan \eqref{eqn:E-line-charge-perp-solution-case-3-L2=0} dan \eqref{eqn:E-line-charge-perp-solution-case-3-L1=0} dengan menerapkan $L = \infty$, yang akan memberikan
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-3-L2-very-long} \vec{E}_q({\rm P}) = \frac{k\lambda}{R} \ \hat{x} + \frac{k\lambda}{R} \ \hat{y} \end{equation}
dan
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-3-L1-very-long} \vec{E}_q({\rm P}) = - \frac{k\lambda}{R} \ \hat{x} + \frac{k\lambda}{R} \ \hat{y}. \end{equation}
Kembali perhatikan bahwa komponen medan listrik pada arah $y$ adalah sama dan pada arah $x$ berbeda tanda pada Persamaan \eqref{eqn:E-line-charge-perp-solution-case-3-L2-very-long} dan \eqref{eqn:E-line-charge-perp-solution-case-3-L1-very-long}.
Kasus terakhir adalah untuk muatan garis berbentuk kawat lurus dengan panjang tak-hingga yang medan listrik di sisinya ingin dicari seperti disajikan pada Gambar 8. Dikarenakan panjang tak-hingga pada kedua sisinya, dapat dianggap posisi titik pengamatan $\rm P$ berada di tengah-tengah panjang kawat.
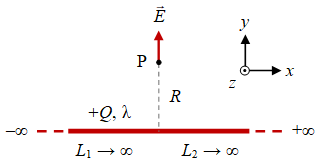
Gambar 8. Medan listrik oleh suatu muatan garis berbentuk kawat tak-berhingga dengan panjang sebelah kiri dan sebelah kanan, dari titik pengamatan $\rm P$ yang berjarak $R$ dari kawat, bernilai $\infty$.
Ketimbang menggunakan Persamaan \eqref{eqn:E-line-charge-perp-solution} untuk kasus ini, lebih cepat bila menggunakan Persamaan \eqref{eqn:E-line-charge-perp-solution-case-2} dan menerapkan $L_1 = L_2 = \infty$ yang akan memberikan
\begin{equation}\label{eqn:E-line-charge-perp-solution-case-4} \vec{E}_q({\rm P}) = \frac{2k\lambda}{R} \ \hat{y}. \end{equation}
Untuk kasus pada sisi di tengah-tengah kawat, seperti diberikan oleh Persamaan Persamaan \eqref{eqn:E-line-charge-perp-solution-case-2} dan \eqref{eqn:E-line-charge-perp-solution-case-4}, komponen pada arah $x$, atau pada arah sejajar panjang kawat, akan bernilai nol karena bagian di sebelah kiri dan kanan titik pengamatan akan saling meniadakan.
— Sparisoma Viridi (@6unpnp) January 10, 2022
electric charge • electric field • charge distribution