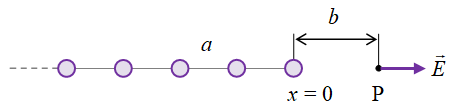
Gambar 1. Sistem rantai muatan 1d dengan jarak antar muatan $a$ dan medan listrik total yang dihasilkannya pada titik $\rm P$.
Sistem kristal paling sederhana yang dapat digunakan untuk menghitung sifat fonon adalah sebuah rantai atom-atom yang berjarak sama yang geraknya dibatasi pada satu-dimensi [1]. Bila atom-atom tersebut kehilangan atau ketambahan elektron akan menjadi ion, sehingga terdapat kristas ion satu-dimensi, yang misalnya ingin dihitung energi kohesinya [2]. Salah satu sistem atom 1d yang ada adalah carbyne, suatu rantai atom-atom karbon yang berikatan ganda atau alternasi ikatan tunggal dan triple, yang sayangnya belum cukup stabil [3] dan telah terdapat perhitungannya menggunakan prinsip pertama [4]. Dalam hal kekuatan tarik spesifik carbyn menggungguli grafena, nanotube karbon, dan intan [5]. Kembali ke sistem ion 1d, walaupun hanya merupakan sistem kristal hipotetical [6], akan tetapi tetap menarik untuk dipelajari dan bermanfaat. Salah satunya adalah saat menyederhanakan analisis dari kisi atom 3d dengan memodelkannya menjadi kisi 1d atau rantai linier, misalnya dalam mempelajari fonon [7].
Untuk saat ini sistem 1d yang akan disinggung dibatasi hanya sampai dua jenis muatan berjarak sama $a$ dan medan listrik yang diamati berada pada jarak $b$ dari muatan paling kanan.

Gambar 1. Sistem rantai muatan 1d dengan jarak antar muatan $a$ dan medan listrik total yang dihasilkannya pada titik $\rm P$.
Alternasi tanda muatan dibatasi hanya sampai bersifat biner, sehingga dapat mengakomodasi hanya muatan positif atau hanya muatan negatif, dan satu muatan positif dan satu muatan negatif berselang-seling. Koordinat $x = 0$ dipilih pada muatan paling kanan.
Sistem dengan satu jenis muatan dapat terbagi atas semua muatan bertanda positif dan semua muatan bertanda negatif.
Sistem rantai 1d muatan positif diberikan pada gambar berikut ini.
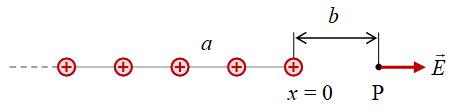
Gambar 2. Sistem rantai muatan 1d dengan jarak antar muatan $a$, semua muatan bertanda positif, dan medan listrik total yang dihasilkannya pada titik $\rm P$.
Posisi muatan $q_i = +Q$ adalah
\begin{equation}\label{eqn:position-positive-mono} \vec{r}_i = (1 - i)a \ \hat{x}, \end{equation}
dengan $i = 1, 2, .., N$ untuk sistem dengan $N$ buah muatan.
Sistem rantai 1d muatan negatif diberikan pada gambar berikut ini.

Gambar 4. Sistem rantai muatan 1d dengan jarak antar muatan $a$, semua muatan bertanda negatif, dan medan listrik total yang dihasilkannya pada titik $\rm P$.
Posisi muatan $q_i = -Q$ adalah
\begin{equation}\label{eqn:position-negative-mono} \vec{r}_i = (1 - i)a \ \hat{x}, \end{equation}
dengan $i = 1, 2, .., N$ untuk sistem dengan $N$ buah muatan.
Untuk sistem dengan dua jenis muatan, saat ini, dibatasi hanya yang berselang-seling satu muatan positif dan satu muatan negatif.
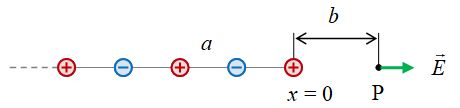
Gambar 4. Sistem rantai muatan 1d dengan jarak antar muatan $a$, tanda muatan berselang-seling positif-negatif, dan medan listrik total yang dihasilkannya pada titik $\rm P$.
Dalam sistem ini diperlukan dua definisi posisi muatan, yaitu untuk muatan positif $q_{2i-1} = +Q$
\begin{equation}\label{eqn:position-bi-positive} \vec{r} _{2i-1} = (2 - 2i)a \ \hat{x}, \end{equation}
dan untuk muatan negatif $q_{2i} = -Q$
\begin{equation}\label{eqn:position-bi-negative} \vec{r} _{2i} = (1 - 2i)a \ \hat{x}, \end{equation}
dengan $i = 1, 2, .., \frac12N$ untuk sistem dengan $N$ buah muatan.
Medan listrik $\vec{E}_i$ oleh satu muatan titik $q_i$, yang terletak di posisi $\vec{r}_i$, diberikan oleh
\begin{equation}\label{eqn:electric-field-point-charge} \vec{E}_i = k \frac{q_i}{|\vec{r} - \vec{r}_i|^3} \ (\vec{r} - \vec{r}_i), \end{equation}
dengan $\vec{r}$ adalah posisi titik amat, yang untuk Gambar 1, 2, 3, dan 4 adalah titik $\rm P$. Koordinat muatan-muatan secara umum berada di kiri titik amat sehingga
\begin{equation}\label{eqn:relative-position} \begin{array}{rcl} \vec{r} - \vec{r}_i & = & (b \ \hat{x}) - (r_i \ \hat{x}) \newline & = & (b - r_i) \ \hat{x}, \newline | \vec{r} - \vec{r}_i | & = & (b - r_i), \end{array} \end{equation}
dengan $\vec{r}_i = r_i \ \hat{x}$. Baris akhir Persamaan \eqref{eqn:relative-position} lebih umumnya adalah $|b - r_i|$, akan tetapi dapat menjadi seperti di atas karena $b > r_i$ dari gambar yang diberikan. Atau dari Persamaan \eqref{eqn:position-positive-mono}, \eqref{eqn:position-negative-mono}, \eqref{eqn:position-bi-positive}, dan \eqref{eqn:position-bi-negative} akan didapatkan $r_i \le 0$.
Substitusi Persamaan \eqref{eqn:relative-position} ke Persamaan \eqref{eqn:electric-field-point-charge} akan menghasilkan
\begin{equation}\label{eqn:electric-field-one-charge} \begin{array}{rcl} \vec{E}_i & = & \displaystyle k \frac{q_i}{(b - r_i)^3} \ (b - r_i) \hat{x} \newline & = & \displaystyle k \frac{q_i}{(b - r_i)^2} \ \hat{x}. \end{array} \end{equation}
Total medan listrik di titik amat $\rm P$ akibat semua muatan menjadi
\begin{equation}\label{eqn:electric-field-all-charges} \begin{array}{rcl} \vec{E} & = & \displaystyle \sum_{i = 1}^N \vec{E}_i \newline & = & \displaystyle \sum _{i = 1}^N k \frac{q_i}{(b - r_i)^2} \ \hat{x}, \newline & = & \displaystyle \hat{x} k \sum _{i = 1}^N \frac{q_i}{(b - r_i)^2}, \end{array} \end{equation}
dengan
\begin{equation}\label{eqn:magnitude-ri} r_i = \vec{r}_i \cdot \hat{x} \end{equation}
menggunakan $\vec{r}_i$ Persamaan \eqref{eqn:position-positive-mono}, \eqref{eqn:position-negative-mono}, \eqref{eqn:position-bi-positive}, dan \eqref{eqn:position-bi-negative}.
— Sparisoma Viridi (@6unpnp) January 15, 2022
electric charge • electric field and source