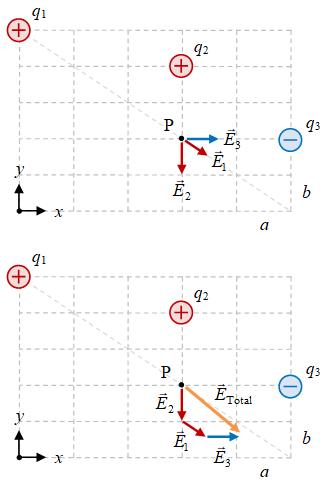
Gambar 1. Beberapa muatan, $q_1$, $q_2$, $q_3$, dalam grid rektilinier, medan listrik yang dihasilkannya, $\vec{E}_1$, $\vec{E}_2$, $\vec{E}_1$, pada suatu titik amat $\rm P$ (atas) dan resultannya $\vec{E} _{\rm Total}$ (bawah).
Medan listrik pada suatu titik amat akibat dua atau lebih muatan merupakan penjumlahan secara vektor dari medan listrik oleh masing-masing muatan pada titik tersebut [1]. Suatu bahan berjenis konduktor mengijinkan muatan bebas untuk bergerak di dalamnya [2] dan telah ditelaah bagaimana distribusi muatan diskrit tersebut pada berbagai bentuk konduktor dua-dimensi yang bersimetri, meliputi elips, hypotrochoid, dan bermacam poligon [3]. Di sini untuk sementara akan dibahas sistem dua dimensi untuk muatan diskrit yang terikat, tidak mudah bergerak, dan medan listrik yang dihasilkannya pada sebuah titik amat tertentu.
Sebuah muatan titik $q_i$ yang berada pada posisi $\vec{r}_i$ akan meyebabkan medan listrik $\vec{E}_i$ berbentuk
\begin{equation}\label{eqn:electric-field-point-charge} \vec{E}_i = k \frac{q_i}{|\vec{r} - \vec{r}_i|^3} \ (\vec{r} - \vec{r}_i), \end{equation}
pada posisi titik amat $\vec{r}$. Untuk sistem 2d, yang sedang dibahas saat ini, baik vektor posisi muatan maupun vektor posisi titik amat akan memiliki komponen pada arah $x$ dan $y$.
Grid rektilinier mirip dengan grid Kartesian, yang lebih fleksibel karena tidak harus berjarak spasi yang sama [4], untuk saat ini tetap dipiih berspasi sama untuk masing-masing $x$ dan $y$, akan tetapi tidak perlu sama antar $x$ dan $y$.

Gambar 1. Beberapa muatan, $q_1$, $q_2$, $q_3$, dalam grid rektilinier, medan listrik yang dihasilkannya, $\vec{E}_1$, $\vec{E}_2$, $\vec{E}_1$, pada suatu titik amat $\rm P$ (atas) dan resultannya $\vec{E} _{\rm Total}$ (bawah).
Posisi muatan dan titik amat dapat dinyatakan dengan kelipatan dari $a$ pada arah $x$ dan $b$ pada arah $y$.
Tabel 1. Koordinat titik dan vektor posisinya pada grid rektilinier.
| Titik | $a$ | $b$ | $\vec{r}$ |
|---|---|---|---|
| $q_1$ | $0$ | $5$ | $5b\vec{y}$ |
| $q_2$ | $3$ | $4$ | $3a\vec{x} + 4b\vec{y}$ |
| $q_3$ | $5$ | $2$ | $5a\vec{x} + 2b\vec{y}$ |
| $\rm P$ | $3$ | $2$ | $3a\vec{x} + 2b\vec{y}$ |
Selanjutnya adalah menggunakan informasi posisi muatan-muatan dan titik amat dari Tabel 1 pada Persamaan \eqref{eqn:electric-field-point-charge} untuk mendapatkan medan listrik pada titik amat $\rm P$ akibat salah satu muatan, yang kemudian ketiganya dijumlahkan untuk mendapatkan resultannya.
Selain grid rektilinier, masih dalam jenis grid teratur atau terstruktur, terdapat grid segitiga dan heksagonal yang penentuan koordinatnya agak sedikit berbeda, menggunakan vektor satuan yang tidak saling tegak lurus [5].
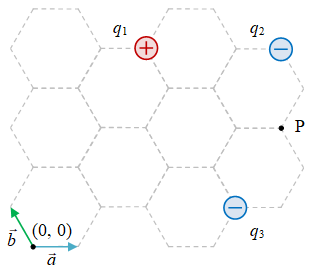
Gambar 2. Beberapa muatan, $q_1$, $q_2$, $q_3$, dalam grid heksagonal dengan vektor gridnya $\vec{a}$, $\vec{b}$, dan suatu titik amat.
Dari Gambar 2 posisi-posisi ketiga muatan dan titik amat belum terlihat jelas, yang dapat diperoleh dengan menggunakan kedua vektor grid $\vec{a}$ dan $\vec{b}$ sebagaimana diberikan pada gambar berikut ini.

Gambar 3. Koordinat ketiga muatan, $q_1$, $q_2$, $q_3$, dan titik amat dalam grid heksagonal dengan vektor gridnya $\vec{a}$, $\vec{b}$.
Pemilihan vektor kisi atau grid tidak unik [6], sehingga pendefinisian yang lain akan menghasilkan nilai koordinat berbeda. Informasi dari Gambar 3 dapat disarikan dalam tabel berikut.
Tabel 2. Koordinat titik dan vektor posisinya pada grid heksagonal.
| Titik | $\vec{a}$ | $\vec{b}$ | $\vec{r}$ |
|---|---|---|---|
| $q_1$ | $5$ | $5$ | $5\vec{a} + 5\vec{b}$ |
| $q_2$ | $8$ | $5$ | $8\vec{a} + 5\vec{b}$ |
| $q_3$ | $5$ | $1$ | $5\vec{a} + \vec{b}$ |
| $\rm P$ | $7$ | $3$ | $7\vec{a} + 3\vec{b}$ |
Dengan menggunakan informasi dari Tabel 2 dapat diperoleh vektor posisi untuk setiap titik muatan dan titik amat, yang kemudian akan digunakan pada Persamaan \eqref{eqn:electric-field-point-charge} untuk mendapatkan medan listrik pada titik amat $\rm P$ akibat salah satu muatan dari $q_1$, $q_2$, atau $q_3$.

Gambar 4. Medan listrik $\vec{E}_1$, $\vec{E}_2$, $\vec{E}_3$, akibat muatan $q_1$, $q_2$, dan $q_3$ di titik amat $\rm P$ dan resultannya $\vec{E} _{\rm Total}$.
Setelah mendapatkan medan listrik akibat masing-masing muatan di titik amat $\rm P$, ketiga medan listrik tesebut dijumlahkan secara vektor untuk mendapatkan medan listrik totalnya.
Vektor kisi menghubungkan dua titik kisi [7], dengan titik kisi adalah suatu titik perpotongan antara dua atau lebih garis grid dalam larik titik-titik yang berjarak teratur [8]. Kembali ke Gambar 2 terdapat setidaknya tiga pasang vektor grid yang dapat digunakan, yang akan memberikan koordinat yang berbeda pada sistem grid heksagonal akan tetapi koordinat yang sama pada sistem koordinat Cartesiannya.

Gambar 5. Grid heksagonal dan tiga pilihan untuk pasangan vektor grid yang berbeda dalam menyatakan titik $\rm A$ dari pusat koordinat $(0, 0)$.
Perbandingan ketig pasang vektor kisi dari Gambar 5 diberikan pada tabel berikut ini.
Tabel 3. Vektor grid heksagonal, koordinat heksagonal, dan vektor posisi dalam sistem koordinat Kartesian.
| $\vec{a}/a$ | $\vec{b}/a$ | ${\rm A}$ | $\vec{r}/a$ |
|---|---|---|---|
| $\hat{x}$ | $-\frac12\hat{x}+\frac12\sqrt{3}\hat{y}$ | $(6, 5)$ | $\frac52\hat{x}+\frac52\sqrt{3}\hat{y}$ |
| $\hat{x}$ | $\frac12\hat{x}+\frac12\sqrt{3}\hat{y}$ | $(0, 5)$ | $\frac52\hat{x}+\frac52\sqrt{3}\hat{y}$ |
| $\frac12\hat{x}+\frac12\sqrt{3}\hat{y}$ | $-\frac12\hat{x}+\frac12\sqrt{3}\hat{y}$ | $(5, 0)$ | $\frac52\hat{x}+\frac52\sqrt{3}\hat{y}$ |
Perhatikan kolom terakhir pada Tabel [3] yang memberikan posisi yang sama menurut koordinat Kartesian. Jadi walaupun vektor grid heksagonal tidak unik akan tetapi tetap memberikan koordinat yang sama.
PDF— Sparisoma Viridi (@6unpnp) January 16, 2022
electric charge • electric field and source