
Gambar 1. Tiga muatan titik $q_1$, $q_2$, $q_3$, dan titik amat $\rm P$ pada titik-titik sudut suatu balok dengan panjang sisi-sisi $a$, $b$, dan $c$.
Dalam pembelajaran perhitungan medan listrik oleh sejumlah titik muatan dalam 3d, salah satu problemnya adalah sistem berbentuk sejumlah muatan yang terletak pada titik-titik sudut sebuah kubus [1]. Visualiasi medan listrik oleh beberapa muatan titik dalam 3d, juga permukaan ekipotensialnya, dapat digambarkan menggunakan software Maple 10 [2]. Dalam aplikasinya medan listrik dalam tiga dimensi menjadi penting sehingga perlu dihitung dan diukur di substation bertegangan tinggi [3] dan dimodelkan untuk membantu analisis pada sistem peringatan petir [4]. Untuk saat ini tiga muatan titik pada sudut-sudut suatu kotak dan kontribusinya pada suatu titik amat akan dibahas sebagai ilustrasi superposisi medan listrik [5], yang dalam hal ini bersumber dari tiga muatan titik. Sistem ini dapat diperluas menjadi bersumber dari $N$ muatan titik.
Sebuah balok persegi panjang dengan panjang sisi-sisi $a$, $b$, dan $c$ merupakan bangun 3d untuk meletakkan tiga muatan titik seperti diberikan pada gambar berikut.

Gambar 1. Tiga muatan titik $q_1$, $q_2$, $q_3$, dan titik amat $\rm P$ pada titik-titik sudut suatu balok dengan panjang sisi-sisi $a$, $b$, dan $c$.
Untuk saat ini ketiga muatan pada Gambar 1 dipilih bertanda positif, walaupun dengan menggunakan Persamaan \eqref{eqn:electric-field-point-charge} tanda muatan cukup digunakan saja, agar semua medan listriknya mengarah keluar dari sumber agar konsisten. Bila kemudian akan digunakan muatan bertanda negatif arah medan listriknya hanya perlu diubah sebaliknya.
Pada posisi $\vec{r}_i$ terdapat sebuah muatan titik $q_i$ yang akan meyebabkan medan listrik $\vec{E}_i$ berbentuk
\begin{equation}\label{eqn:electric-field-point-charge} \vec{E}_i = k \frac{q_i}{|\vec{r} - \vec{r}_i|^3} \ (\vec{r} - \vec{r}_i), \end{equation}
pada posisi titik amat $\vec{r}$. Baik vektor posisi muatan titik maupun vektor posisi titik amat, keduanya akan memiliki komponen pada arah $x$, $y$ dan $z$.
Medan listrik oleh muatan $q_1$ diilustrasikan pada gambar berikut.

Gambar 2. Medan listrik $\vec{E}_1$ akibat muatan titik $q_1$ pada titik amat $\rm P$.
Dari Gambar 2 dapat diperoleh
\begin{equation}\label{eqn:q1-rel-pos} \begin{array}{rcl} \vec{r} - \vec{r}_1 & = & (a\hat{x} + c\hat{z}) - (c\hat{z}) \newline & = & a\hat{x}, \newline | \vec{r} - \vec{r}_1 | & = & a. \end{array} \end{equation}
Substitusi Persamaan \eqref{eqn:q1-rel-pos} ke Persamaan \eqref{eqn:electric-field-point-charge} akan menghasilkan
\begin{equation}\label{eqn:q1-e-field} \begin{array}{rcl} \vec{E}_1 & = & \displaystyle k \frac{q_1}{|\vec{r} - \vec{r}_1|^3} \ (\vec{r} - \vec{r}_1) \newline & = & \displaystyle k \frac{q_1}{a^3} \ (a\hat{x}) \newline & = & \displaystyle \left( k \frac{q_1}{a^2} \right) \hat{x}, \end{array} \end{equation}
yang merupakan medan listrik oleh muatan $q_1$.
Medan listrik oleh muatan $q_2$ diilustrasikan pada gambar berikut.
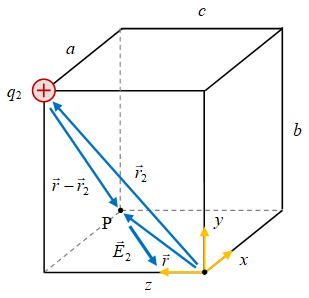
Gambar 3. Medan listrik $\vec{E}_2$ akibat muatan titik $q_2$ pada titik amat $\rm P$.
Dari Gambar 3 dapat diperoleh
\begin{equation}\label{eqn:q2-rel-pos} \begin{array}{rcl} \vec{r} - \vec{r}_2 & = & (a\hat{x} + c\hat{z}) - (b\hat{y} + c\hat{z}) \newline & = & a\hat{x} - b\hat{y}, \newline | \vec{r} - \vec{r}_2 | & = & (a^2 + b^2)^{1/2}. \end{array} \end{equation}
Substitusi Persamaan \eqref{eqn:q2-rel-pos} ke Persamaan \eqref{eqn:electric-field-point-charge} akan menghasilkan
\begin{equation}\label{eqn:q2-e-field} \begin{array}{rcl} \vec{E}_2 & = & \displaystyle k \frac{q_2}{|\vec{r} - \vec{r}_2|^3} \ (\vec{r} - \vec{r}_2) \newline & = & \displaystyle k \frac{q_2}{(a^2 + b^2)^{3/2}} \ (a\hat{x} - b\hat{y}) \newline & = & \displaystyle k \frac{q_2}{a^2 + b^2} \ \left(\frac{a}{\sqrt{a^2 + b^2}} \hat{x} - \frac{b}{\sqrt{a^2 + b^2}} \hat{y} \right) \newline & = & \displaystyle \left[ k \frac{aq_2}{(a^2 + b^2)^{3/2}} \right] \hat{x} - \left[ k \frac{bq_2}{(a^2 + b^2)^{3/2}} \right] \hat{y}, \end{array} \end{equation}
yang merupakan medan listrik oleh muatan $q_2$.
Medan listrik oleh muatan $q_3$ diilustrasikan pada gambar berikut.
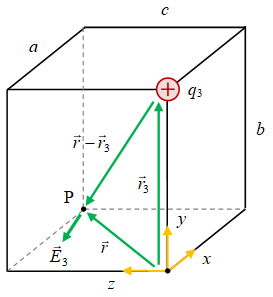
Gambar 4. Medan listrik $\vec{E}_3$ akibat muatan titik $q_3$ pada titik amat $\rm P$.
Dari Gambar 4 dapat diperoleh
\begin{equation}\label{eqn:q3-rel-pos} \begin{array}{rcl} \vec{r} - \vec{r}_3 & = & (a\hat{x} + c\hat{z}) - (b\hat{y}) \newline & = & a\hat{x} - b\hat{y} + c\hat{z}, \newline | \vec{r} - \vec{r}_3 | & = & (a^2 + b^2 + c^2)^{1/2}. \end{array} \end{equation}
Substitusi Persamaan \eqref{eqn:q3-rel-pos} ke Persamaan \eqref{eqn:electric-field-point-charge} akan menghasilkan
\begin{equation}\label{eqn:q3-e-field} \begin{array}{rcl} \vec{E}_3 & = & \displaystyle k \frac{q_3}{|\vec{r} - \vec{r}_3|^3} \ (\vec{r} - \vec{r}_3) \newline & = & \displaystyle k \frac{q_3}{(a^2 + b^2 + c^2)^{3/2}} \ (a\hat{x} - b\hat{y} + c\hat{z}) \newline & = & \displaystyle k \frac{q_3}{a^2 + b^2 + c^2} \ \left( \frac{a}{\sqrt{a^2 + b^2 + c^2}} \hat{x} \right. \newline && \displaystyle \left. - \frac{b}{\sqrt{a^2 + b^2 + c^2}} \hat{y} + \frac{c}{\sqrt{a^2 + b^2 + c^2}} \hat{z} \right) \newline & = & \displaystyle \left[ k \frac{aq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{x} \newline && \displaystyle - \left[ k \frac{bq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{y} \newline && \displaystyle + \left[ k \frac{cq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{z}, \end{array} \end{equation}
yang merupakan medan listrik oleh muatan $q_1$.
Medan listrik oleh ketiga muatan $q_1$, $q_2$, $q_3$ diilustrasikan pada gambar berikut.

Gambar 5. Medan listrik $\vec{E} _{\rm Total}$ akibat muatan titik $q_1$, $q_2$, $q_3$ pada titik amat $\rm P$.
Dengan menjumlahkan Persamaan \eqref{eqn:q1-e-field}, \eqref{eqn:q2-e-field}, dan \eqref{eqn:q3-e-field} dapat diperoleh
\begin{equation}\label{eqn:total-e-field} \begin{array}{rcl} \vec{E} _{\rm Total} & = & \vec{E}_1 + \vec{E}_2 + \vec{E}_3 \newline & = & \displaystyle \left( k \frac{q_1}{a^2} \right) \hat{x} \newline && \displaystyle + \left[ k \frac{aq_2}{(a^2 + b^2)^{3/2}} \right] \hat{x} - \left[ k \frac{bq_2}{(a^2 + b^2)^{3/2}} \right] \hat{y} \newline && \displaystyle + \left[ k \frac{aq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{x} \newline && \displaystyle - \left[ k \frac{bq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{y} \newline && \displaystyle + \left[ k \frac{cq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{z} \newline & = & \displaystyle k \left[ \frac{aq_1}{(a^2)^{3/2}} + \frac{aq_2}{(a^2 + b^2)^{3/2}} + \frac{aq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{x} \newline && \displaystyle - k \left[ \frac{bq_2}{(a^2 + b^2)^{3/2}} + \frac{bq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{y} \newline && \displaystyle + k \left[ \frac{cq_3}{(a^2 + b^2 + c^2)^{3/2}} \right] \hat{z}, \end{array} \end{equation}
yang merupakan medan listrik total $\vec{E} _{\rm Total}$ akibat ketiga muatan $q_1$, $q_2$, $q_3$.
PDF— Sparisoma Viridi (@6unpnp) January 16, 2022
electric charge • electric field and source