
Gambar 1. Benda menempuh gerak parabola di atas bidang mendatar dengan $\tan\theta = 4/3$, $v_0 = 50$, $x_0 = 0$, $y_0 = 10$, dan $g = 10$.
Dalam matematika akar merupakan suatu solusi dari suatu persamaan, yang biasanya dinyatakan sebagai angka atau formula aljabar [1]. Solusi yang dimaksud adalah membuat suatu persamaan menjadi bernilai nol sehingga sering dikatakan sebagai pembuat nol [2]. Namun agar diperhatikan bahwa terdapat penggunaan kata akar sebagai cara ringkas untuk menyatakan akar kuadrat [3]. Terdapat berbagai algoritma untuk mencari akar suatu persamaan dengan salah satu penggolongannya adalah metode kurung, interpolasi, metode iteratif, dan kombinasi berbagai metode [4]. ROOT suatu framework analisis data sumber-terbuka, ditulis utamanya dalam C++, yang digunakan dalam fisika energi tinggi dan lainnya menyediakan kelas pencarian akar satu dimensi [5], sebagaimana SciPy suatu piranti lunak sumber-terbuka, berbasiskan Python, untuk matematika, sains, dan rekayasa yang menyediakan setidaknya delapan algoritma untuk mencari akar suatu fungsi skalar [6]. Atau dapat pula suatu program dituliskan dalam Python tanpa perlu impor modul apapun [7].
Bila $x_1$ merupakan akar dari suatu persamaan $f(x)$ maka hubungan
\begin{equation}\label{eqn:root-of-f(x)} f(x_1) = 0 \end{equation}
harus terpenuhi. Selain itu menyelesaikan persamaan
\begin{equation}\label{eqn:root-of-g(x)-h(x)} g(x) = h(x), \end{equation}
merupakan hal yang sama karena dapat dibentuk
\begin{equation}\label{eqn:root-of-f(x)=g(x)-h(x)} f(x) = g(x) - h(x), \end{equation}
sehingga solusi dari Persamaan \eqref{eqn:root-of-f(x)} juga merupakan solusi dari Persamaan \eqref{eqn:root-of-g(x)-h(x)} melalui hubungan pada Persamaan \eqref{eqn:root-of-f(x)=g(x)-h(x)}. Atau dapat pula dikatakan bahwa bentuk Persamaan \eqref{eqn:root-of-g(x)-h(x)} akan menjadi seperti pada Persamaan \eqref{eqn:root-of-f(x)} bila dipilih $h(x) = 0$.
Benda yang dilemparkan dengan sudut peluncuran (en: launch angle) $\theta$ dan menempuh gerak parabola merupakan contoh yang akrab untuk aplikasi pencari akar suatu persamaan. Mencari kapan benda kembali menyentuh lantai mendatar merupakan pemanfaatkan dari Persamaan \eqref{eqn:root-of-f(x)}, sedangkan untuk sistem yang sama akan tetapi dengan lantai miring dengan sudut inklinasi $\beta$ tertentu merupakan penerapan Persamaan \eqref{eqn:root-of-f(x)=g(x)-h(x)}.
Dengan kecepatan awal benda $v_0$, sudut peluncuran $\theta$, posisi awal $(x_0, y_0)$ maka lintasan benda diperoleh berbentuk parabolik terbuka ke bawah atau lintasan peluru
\begin{equation}\label{eqn:parabolic-trajectory-y-x} p(x) = y = c_0 + c_1 \ x + c_2 \ x^2, \end{equation}
dengan
\begin{equation}\label{eqn:projectile-trajectory-y-x-c0} c_0 = y_0 - \tan\theta \ x_0 - \frac{g x_0^2}{2 v_0^2 \cos^2\theta}, \end{equation}
\begin{equation}\label{eqn:projectile-trajectory-y-x-c1} c_1 = \tan\theta - \frac{g x_0}{v_0^2 \cos^2\theta}, \end{equation}
\begin{equation}\label{eqn:projectile-trajectory-y-x-c2} c_2 = -\frac{g}{2 v_0^2 \cos^2\theta}. \end{equation}
Dan secara umum bidang lantai dapat dipilih berbentuk linier atau bidang miring atau menanjak (en: incline)
\begin{equation}\label{eqn:incline} i(x) = m(x - x_0) + y_0, \end{equation}
yang juga lewat titik $(x_0, y_0)$.
Gerak parabola yang umum diperoleh saat benda dilemparkan di atas bidang mendatar dengan sudut luncur $\theta$ dan kecepatan awal $v_0$. Posisi titik awal $(x_0, y_0)$ biasanya berada pada bidang mendatar tersebut.

Gambar 1. Benda menempuh gerak parabola di atas bidang mendatar dengan $\tan\theta = 4/3$, $v_0 = 50$, $x_0 = 0$, $y_0 = 10$, dan $g = 10$.
Menggunakan Persamaan \eqref{eqn:projectile-trajectory-y-x-c0}, \eqref{eqn:projectile-trajectory-y-x-c1}, dan \eqref{eqn:projectile-trajectory-y-x-c2}, serta informasi pada keterangan Gambar 1 dapat diperoleh
\begin{equation}\label{eqn:projectile-trajectory-y-x-c0-level} \begin{array}{rcl} c_0 & = & \displaystyle 10 - (\tfrac43)(0) - \frac{(10)(0)^2}{2 (50)^2 (3/5)^2} \newline & = & 10 - 0 - 0 \newline & = & 10, \end{array} \end{equation}
\begin{equation}\label{eqn:projectile-trajectory-y-x-c1-level} \begin{array}{rcl} c_1 & = & \displaystyle \tfrac43 - \frac{(10) (0)}{(50)^2 (3/5)^2} \newline & = & \tfrac43 - 0 \newline & = & \tfrac43, \end{array} \end{equation}
\begin{equation}\label{eqn:projectile-trajectory-y-x-c2-level} \begin{array}{rcl} c_2 & = & \displaystyle -\frac{g}{2 v_0^2 \cos^2\theta} \newline & = & \displaystyle -\frac{10}{2 (50)^2 (3/5)^2} \newline & = & \displaystyle -\frac{10}{2 (2500) (9/25)} \newline & = & \displaystyle -\frac{10}{1800} \newline & = & - 0.00556, \end{array} \end{equation}
sehingga
\begin{equation}\label{eqn:parabolic-trajectory-y-x-level} p(x) = -0.00556 \ x^2 + \tfrac43 \ x + 10, \end{equation}
seperti dalam Gambar 1. Dan dengan
\begin{equation}\label{eqn:level-plane} i(x) = 10 \end{equation}
maka persoalan akar yang dicari adalah
\begin{equation}\label{eqn:parabolic-level-equation} \begin{array}{rcl} f(x) & = & 0 \newline p(x) - i(x) & = & 0 \newline (-0.00556 \ x^2 + \tfrac43 \ x + 10) - (10) & = & 0 \newline -0.00556 \ x^2 + \tfrac43 \ x & = & 0. \end{array} \end{equation}
Solusi dari Persamaan \eqref{eqn:parabolic-level-equation} adalah $x_1 = 0$ yang merupakan titik awal lintasan parabola dan $x_2 = (\frac43)/0.00556 \approx 240$ seperti terlihat pada Gambar 1.
Gerak parabola yang lain adalah saat benda dilemparkan di atas bidang miring. Parameter benda meliputi sudut luncur $\theta$ dan kecepatan awal $v_0$, sedangkan untuk bidang miringnya perlu sudut inklinasi $\beta$. Kembali posisi titik awal $(x_0, y_0)$ biasanya berada pada bidang miring tersebut.
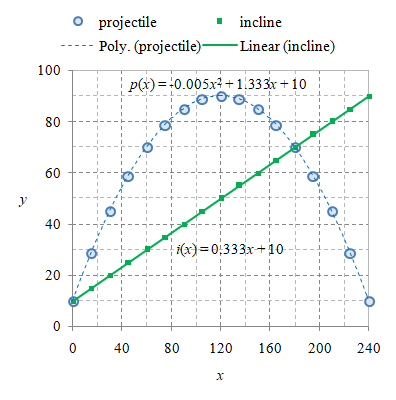
Gambar 2. Benda menempuh gerak parabola di atas bidang miring dengan $\tan\theta = 4/3$, $v_0 = 50$, $x_0 = 0$, $y_0 = 10$, dan $g = 10$, serta $\tan\beta = 1/3$.
Untuk kasus ini Persamaan \eqref{eqn:parabolic-trajectory-y-x-level} kembali digunakan, dan dengan
\begin{equation}\label{eqn:inclined-plane} i(x) = \frac13 \ x + 10 \end{equation}
akan membuat Persamaan \eqref{eqn:parabolic-level-equation} menjadi
\begin{equation}\label{eqn:parabolic-incline-equation} \begin{array}{rcl} f(x) & = & 0 \newline p(x) - i(x) & = & 0 \newline (-0.00556 \ x^2 + \tfrac43 \ x + 10) - (\frac13 \ x + 10) & = & 0 \newline -0.00556 \ x^2 + x& = & 0. \end{array} \end{equation}
Kembali diperoleh dua titik sebagai solusi dari Persaamaan \eqref{eqn:parabolic-incline-equation} yaitu $x_1 = 0$ dan $x_2 = 1 / 0.00556 \approx 180$ seperti ditunjukkan pada Gambar 2.
Gerak parabola yang jarang ada adalah saat benda dilemparkan di atas bidang yang bergelombang. Parameter benda masih meliputi sudut luncur $\theta$ dan kecepatan awal $v_0$, sedangkan untuk bidang bergelombangnya perlu persaman $i(x)$ Kembali digunakan posisi titik awal $(x_0, y_0)$ biasanya berada pada bidang bergelombang tersebut.

Gambar 3. Benda menempuh gerak parabola di atas bidang bergelombang dengan $\tan\theta = 4/3$, $v_0 = 50$, $x_0 = 0$, $y_0 = 10$, dan $g = 10$.
Pada Gambar 3 digunakan persamaan untuk bidang bergelombang dalam bentuk
\begin{equation}\label{eqn:wavy-plane} i(x) = 10 + 10\sin(2\pi/200) \cdot 0.012x, \end{equation}
yang akan memberikan solusi pada posisi $x_1 = 0$ dan sekitar $x_2 = 225$ menurut Gambar 3.
Selain gerak parabola, sistem fisis yang memerlukan konsep akar adalah peristiwa sebuah mobil menyusul mobil di depannya, peristiwa tumbukan antara dua bukan benda titik, penentuan titik pantul suatu berkas cahaya yang menuju cermin, gerak memantul bola pada lantai bergelombang, dan lain-lain.
— Sparisoma Viridi (@6unpnp) January 22, 2022