gaussian surface

Saat membicarakan hukum Gauss, terdapat konsep permukaan Gauss yang merupakan suatu permukaan khayal [1], suatu konstruksi matematika yang dapat berbentuk permukaan berbentuk apa saja asalkan tertutup, yang dalam implementasinya untuk meghitung fluks dengan permukaan, akan lebih mudah diselesaikan bila bentuk permukaan yang dipilih memiliki simetri tertentu [2]. Permukaan tertutup bukan merupakan permukaan Gauss walaupun permukaan dengan luas tak-hingga dapat merupakan pendekatan permukaan Gauss [3]. Terdapat pemahaman bahwa sudut antara suatu permukaan Gauss dengan medan listirk yang menembusnya perlu selalu tetap [4], yang tepat bila tujuan utama hukum ini adalah untuk memperoleh medan listrik dari distribusi muatan yang terlingkupi permukaan tertutup [5]. Akan tetapi bukan hanya itu pemanfaatan dari hukum Gauss sebenarnya. Terdapat pula informasi bahwa hukum Gauss dapat diterapkan untuk distribusi medan listrik oleh muatan cincin [6], yang seharusnya memerlukan syarat simetri untuk analisis Gauss agar produktif, kecuali bila merupakan penerapan solusi analisis beda hingga [7].

closed surface

Permukaan Gauss harus merupakan permukaan tertutup, baik merupakan suatu permukaan yang dapat diungkapkan dengan satu fungsi ataupun merupakan gabungan dari beberapa permukaan.

Gambar 1. Suatu permukaan Gauss: (a) berbentuk kotak tertutup yang terdiri dari enam bidang datar, dan (b) terbagi menjadi bagian kiri (L: left) dan kanan (R: right).

Enam bidang datar terbatas berbentuk persegi panjang dapat digunakan untuk membentuk kotak tertutup yang merupakan suatu permukaan Gauss seperti diberikan pada Gambar 1. Dalam hal ini integral pada gambar tersebut dapat menjadi penjumlahan luas enam bidang

\begin{equation}\label{eqn:gaussian-surface-box} \begin{array}{rcl} S & = & \oint dS \newline & = & \displaystyle \sum_{i = 1}^6 S_i \newline & = & (S_3 + S_4 + S_5) + (S_1 + S_2 + S_6) \newline & = & S_L + S_R, \end{array} \end{equation}

yang dapat dibagi menjadi bagian kiri dan kanan. Pembagian menjadi dua bagian ini hanya untuk memperjelas bila ada muatan di dalamnya kelak.

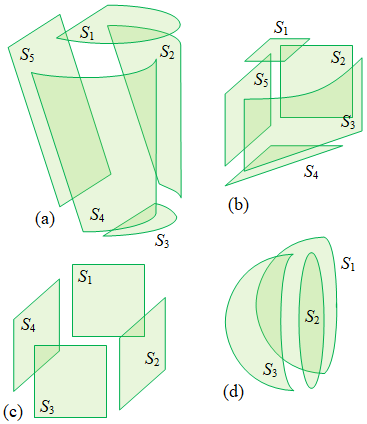
Gambar 2. Beberapa bentuk permukaan yang membentuk ruang di antaranya.

Gabungan beberapa permukaan dengan fungsi tertentu dapat membentuk suatu ruang di antara permukaan-permukaan tersebut seperti diberikan pada Gambar 2. Perlu kejelia untuk melihat apakah permukaan-permukaan tersebut dapat digunakan sebagai permukaan Gauss.

enclosed charge

Setelah memahami syarat suatu permukaan Gauss, pengertian berikutnya yang perlu dipahami adalah muatan yang terlingkupi atau berada di dalam permukaan Gauss.

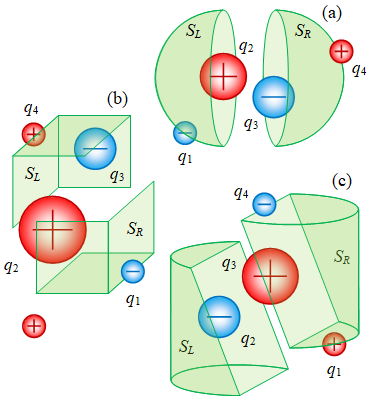
Gambar 3 Empat muatan dan permukaan Gauss berbentuk: (a) kulit bola, (b) kotak, dan (c) silinder.

Muatan-muatan pada Gambar 3 berada keseluruhannya di dalam atau di luar permukaan Gauss. Pada aplikasinya tidak perlu selalu demikian.

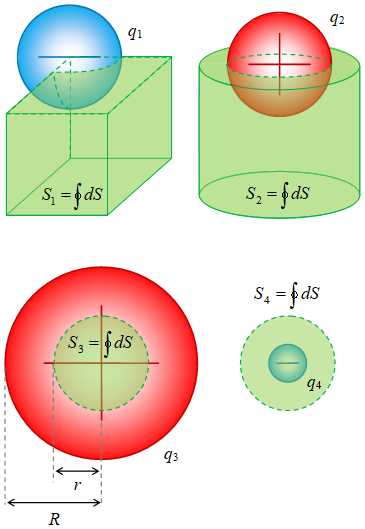
Gambar 4. Sebuah muatan $q_i$, $i = 1, .., 4$, berbentuk bola pejal dan permukaan Gauss yang digunakan padanya berbentuk kotak untuk $q_1$, silinder untuk $q_2$, bola untuk $q_3$ ddan $q_4$.

Ada kalanya permukaan Gauss tidak melingkupi seluruh bagian muatan akan tetapi hanya sebagiannya. Contoh-contoh kasus ini diberikan pada Gambar 4.

exer

1. Manakah permukaan pada Gambar 2 yang dapat digunakan sebagai suatu permukaan Gauss?
2. Tentukan muatan yang terlingkupi oleh permukaan Gauss pada Gambar 3(b).
3. Tentukan mautan yang tidak terlingkupi oleh permukaan Gauss pada Gambar 3(a).
4. Tentukan muatan yang terlingkupi oleh permukaan Gauss yang beririsan dengan muatan $q_1$ pada Gambar 4.
5. Tentukan muatan yang terlingkupi oleh permukaan Gauss yang beririsan dengan muatan $q_3$ pada Gambar 4. Asumsikan berapat muatan volume $\rho$ seragam.

note

1. Carl R. Nave, “Gaussian Surfaces”, HyperPhysics, 2017, url http://hyperphysics.phy-astr.gsu.edu/hbase/electric/gausur.html#c1 [20220123]
2. Samuel J. Ling, Jeff Sanny, Bill Moebs, Many Contributing Authors, “Explaining Gauss’s Law”, University Physics, OpenStax, 6 Nov 2020, url https://phys.libretexts.org/@go/page/4380 [20220123].
3. Wikipedia contributors, ‘Gaussian surface’, Wikipedia, The Free Encyclopedia, 28 March 2021, 03:22 UTC, url https://en.wikipedia.org/w/index.php?oldid=1014613716 [20220123].
4. Student Baba, “Gaussian Surface and Steps to Determine a Gaussian Surface with Examples”, The Student Baba, 15 Sep 2019, url https://student-baba.com/gaussian-surface-and-steps-to-determine-a-gaussian-surface-with-examples/ [20220123].
5. Sanjay knowledge, “What is the importance of Gauss law?”, Actingcolleges.org, 22 Nov 2021, url https://actingcolleges.org/library/acting-questions/read/92086-what-is-the-importance-of-gauss-law [20220123].
6. Admin, “Gauss Law - Applications, Gauss Theorem Formula”, BYJUS, 28 Jun 2021, url https://byjus.com/jee/gauss-law/ [20220123].
7. Brad Barkert, “Answer to ‘How do I find the electric field of a circular ring using Gauss’s law?’”, Quora, 6 Dec 2018, url https://www.quora.com/How-do-I-find-the-electric-field-of-a-circular-ring-using-Gauss-s-law/answer/Brad-Barker-24 [20220123].

comments

#bug0410

— Sparisoma Viridi (@6unpnp) January 23, 2022