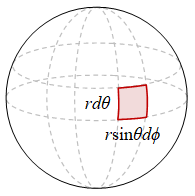
Gambar 1. Elemen luas kulit bola berjari-jari $r$.
Suatu fungsi $f: \mathbb{R}^n \rightarrow \mathbb{R}$ merupakan simetri bola bila fungsi tersebut bernilai tetap pada setiap bola yang berpusat di titik origin, dengan nilai tetap ini masih dapat merupakan fungsi dari jarak ke titik origin atau $r$ [1]. Dalam biolog simetri bola merupakan simetri yang dikenal selain bilateral dan radial, di mana hanya kelompok protozoa, Radiolaria dan Heliozoia yang menggambarkan simetri bola [2]. Istilah ini digunakan untuk mendeskripsikan geometri bintang dan planet dalam relativitas umum, untuk bumi misalnya bisa dianggap bersimetri bola maka akan diperoleh formulasi matematika yang sederhana untuk medan gravitasinya [3]. Pontesial suatu gaya sentral merupakan medan skalar dengan simetri bola dan gayanya sendiri merupakan medan vektor dengan simetri bola yang besar dan arahnya (keluar atau ke dalam saja) bergantung pada jarak dari titik origin [4]. Untuk memperoleh medan listrik dengan hukum Gauss perlu memperhatikan simetri dari distribusi muatan untuk disesuaikan dengan bentuk permukaan Gaussnya [5], yang dalam hal ini yang memiliki simetri bola.
Sistem-sistem muatan yang memiliki simetri bola adalah satu muatan titik, kulit bola, bola pejal (isolator, konduktor), bola berongga (isolator, konduktor), bola berongga (isolator, konduktor) dengan muatan titik di tengah-tengah rongga.
Bentuk medan listrik yang dapat diperoleh berbantuan hukum Gauss dengan permukaan Gauss bersimetri bola dibatasi pada
\begin{equation}\label{eqn:electric-field-spherical-symmetry} \vec{E} = E \ \hat{r}, \end{equation}
dengan medan listriknya
\begin{equation}\label{eqn:electric-field-radial-only} E = E(r) \ne E(\theta, \phi), \end{equation}
hanya diperboleh fungsi dari $r$ dan tidak boleh merupakan fungsi dari $\theta$ dan $\phi$. Dalam penerapan hukum Gauss medan listrik telah diasumsikan memenuhi Persamaan \eqref{eqn:electric-field-spherical-symmetry} dan \eqref{eqn:electric-field-radial-only} dan yang akan dicari adalah bentuk fungsinya $E = E(r)$.
Permukaan Gauss bersimetri bola adalah kulit bola dengan jari-jari $r$.

Gambar 1. Elemen luas kulit bola berjari-jari $r$.
Elemen luas kulit bola secara umum adalah
\begin{equation}\label{eqn:spherical-surface-element} d\vec{A} = \hat{r} \ dA = \hat{r} \ (rd\theta)(r\sin\theta d\phi), \end{equation}
akan tetapi dengan simetri bola akan menjadi
\begin{equation}\label{eqn:spherical-surface-element-symmetry} \int d\vec{A} = \hat{r} \ r^2 \int \sin\theta d\theta \int d\phi = \hat{r} \ 4\pi r^2, \end{equation}
dengan batas integral $d\theta$ dari $0$ sampai $\pi$ dan $d\phi$ dari $0$ sampai $2\pi$.
Dengan melihat bentuk medan listrik seperti pada Persamaan \eqref{eqn:electric-field-spherical-symmetry} dan \eqref{eqn:electric-field-radial-only} sementara elemen luasnya adalah seperti pada Persamaan \eqref{eqn:spherical-surface-element}, maka fungsi medan listrik $E(r)$ dapat keluar dari integral karena bukan fungsi dari $\theta$ dan $\phi$ sehingga penyelesaiannya akan menjadi sederhana untuk
\begin{equation}\label{eqn:gauss-law-integral} \int \vec{E} \cdot d\vec{A} = E \ (4\pi r^2), \end{equation}
dengan menggunakan $\hat{r} \cdot \hat{r} = 1$.
— Sparisoma Viridi (@6unpnp) January 29, 2022