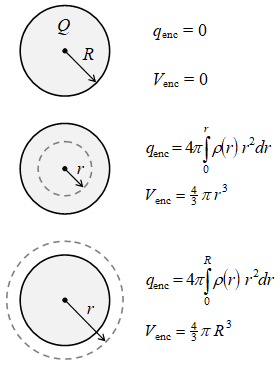
Gambar 1. Bola pejal bermuatan seragam dengan permukaan Gaussnya.
Pemilihan permukaan Gauss yang bersesuaian dengan simetri medan listrik yang disebabkan oleh distribusi muatan akan membuat integrasinya dapat dilakukan untuk memperoleh medan listriknya [1].
Sebuah bola pejal bermuatan total $Q$ dengan rapat muatan seragam yang terletak di origin akan memberikan medan listrik pada setiap titik di sekitarnya dalam bentuk
\begin{equation}\label{eqn:electric-field-form} \vec{E} = E(r) \ \hat{r} \end{equation}
yang menggambarkan simetri bola. Untuk bola pejal berbahan isolator permukaan Gauss dan muatan yang terlingkupinya untuk kedua rentang jarak dari origin $r$ diberikan pada gambar berikut.
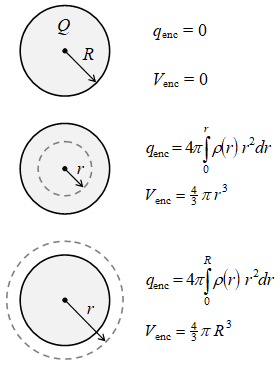
Gambar 1. Bola pejal bermuatan seragam dengan permukaan Gaussnya.
Permukaan Gauss yang dipilih berbentuk
\begin{equation}\label{eqn:gaussian-surface} \begin{array}{rcl} \displaystyle \oint d\vec{A} & = & \displaystyle \oint \hat{r} \ dA \newline & = & \displaystyle \int_0^\pi \int_0^{2\pi} \hat{r} \ (r d\theta) (r \sin\theta d\phi) \newline & = & \displaystyle \hat{r} \ r^2 \int_0^\pi \sin\theta d\theta \int_0^{2\pi} d\phi \newline & = & \hat{r} \ 4\pi r^2. \end{array} \end{equation}
Muatan yang terlingkupi untuk kasus silinder pejal berbahan isolator yang berapat muatan seragam terbagi menjadi dua bagian, yaitu
\begin{equation}\label{eqn:enclosed-charge} q_{\rm enc} = \left\{ \begin{array}{cc} \displaystyle Q \frac{r^3}{R^3}, & 0 \le r \le R, \newline Q, & R \le 0, \end{array} \right. \end{equation}
seperti diilusrasikan pada Gambar 1. Persamaan \eqref{eqn:enclosed-charge} berlaku untuk $\rho$ bernilai tetap atau rapat muatan seragam atau $\rho \ne \rho(r)$. Dengan demikian saat menggunakan hukum Gauss dengan menerapkan Persamaan \eqref{eqn:electric-field-form}, \eqref{eqn:gaussian-surface}, dan \eqref{eqn:enclosed-charge} perlu dibagi dalam rentang $0 \le r \le R$ dan $R \le r$. Untuk rentang $0 \le r \le R$
\begin{equation}\label{eqn:gauss-law-solid-sphere-inner} \begin{array}{rcl} \displaystyle \oint \vec{E} \cdot d\vec{A} & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline \displaystyle \oint E(r) \ \hat{r} \cdot \hat{r} \ dA & = & \newline \displaystyle \oint E(r) dA & = & \newline \displaystyle \oint E(r) (r d\theta) (r \sin\theta d\phi) & = & \newline \displaystyle E(r) \ r^2 \oint \sin\theta d\theta d\phi & = & \newline \displaystyle E(r) \ r^2 \int_0^\pi \sin\theta d\theta \int_0^{2\pi} d\phi & = & \newline E(r) \ r^2 \ (2) \ (2\pi) & = & \newline E(r) & = & \displaystyle \frac{1}{4\pi r^2} \frac{(Qr^3/R^3)}{\varepsilon_0} \newline & = & \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{R^2} \ \frac{r}{R}, \end{array} \end{equation}
dan untuk $R \le r$ hanya berbeda di tiga baris terakhir
\begin{equation}\label{eqn:gauss-law-solid-sphere-outter} \begin{array}{rcl} \displaystyle \oint \vec{E} \cdot d\vec{A} & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline E(r) \ r^2 \ (2) \ (2\pi) & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline E(r) & = & \displaystyle \frac{1}{4\pi r^2} \frac{Q}{\varepsilon_0} \newline & = & \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{r^2}. \end{array} \end{equation}
Dengan menggunakan hasil dari Persamaan \eqref{eqn:gauss-law-solid-sphere-inner} dan \eqref{eqn:gauss-law-solid-sphere-outter} dapat digabungkan menjadi
\begin{equation}\label{eqn:gauss-law-solid-sphere} E(r) = \left\{ \begin{array}{cc} \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{R^2} \ \frac{r}{R}, & 0 \le r \le R, \newline \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{r^2}, & R \le r, \newline \end{array} \right. \end{equation}
yang merupakan medan listrik akibat sebuah bola pejal berbahan konduktor dengan muatan seragam $\rho = Q/V$.
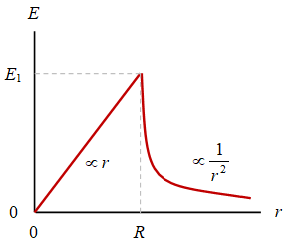
Gambar 2. Medan listrik $E$ sebagai fungsi jarak $r$ dari pusat origin untuk bola pejal yang terbuat dari isolator bermuatan seragam.
Ilustrasi grafik medan listrik $E$ sebagai fungsi jarak dari origin $r$ diberikan pada Gambar 1 dengan $E_1 = (1/4\pi\varepsilon_0)(Q/R^2)(r/R)$ yang merupakan suku pada Persamaan \eqref{eqn:gauss-law-solid-sphere} untuk bagian dalam bola pejal.
— Sparisoma Viridi (@6unpnp) January 30, 2022