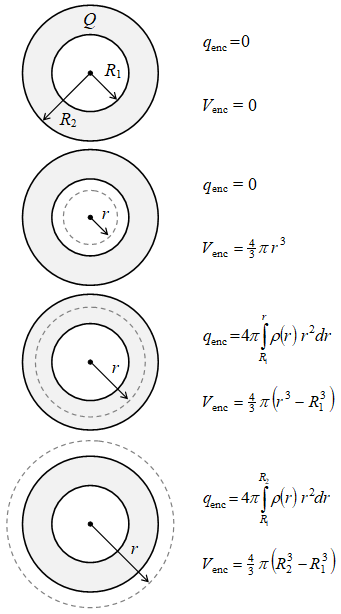
Gambar 1. Bola berongga bermuatan seragam dengan permukaan Gaussnya.
Agar integrasi dapat dilakukan sehingga dapat memperoleh medan listrik dengan menggunakan hukum Gauss, perlu dipilih permukaan Gauss yang sesuai dengann simetri medan listrik yang disebabkan oleh distribusi muatan penyebabnya [1].
Suatu bola berongga dengan jari-jari dalam $R_1$ dan jari-jari luar $R_2$ terbuat dari bahan isolator dengan rapat muatan seragam $\rho \ne \rho(r, \theta, \phi)$ atau bernilai konstan, permukaan Gauss yang dipilih untuk berbagai nilai $r$, volumenya, dan muatan yang terlingkupinya diberikan pada gambar di bawah ini.

Gambar 1. Bola berongga bermuatan seragam dengan permukaan Gaussnya.
Dengan pusat bola berongga terletak di pusat origin dan $\rho \ne \rho(r, \theta, \phi)$ maka akan memberikan medan listrik pada setiap titik di sekitarnya dalam bentuk
\begin{equation}\label{eqn:electric-field-form} \vec{E} = E(r) \ \hat{r} \end{equation}
yang menggambarkan simetri bola. Dengan demikian permukaan Gauss yang dipilih pun berbentuk bola dengan elemen luasnya
\begin{equation}\label{eqn:gaussian-surface} \begin{array}{rcl} \displaystyle \oint d\vec{A} & = & \displaystyle \oint \hat{r} \ dA \newline & = & \displaystyle \int_0^\pi \int_0^{2\pi} \hat{r} \ (r d\theta) (r \sin\theta d\phi) \newline & = & \displaystyle \hat{r} \ r^2 \int_0^\pi \sin\theta d\theta \int_0^{2\pi} d\phi \newline & = & \hat{r} \ 4\pi r^2. \end{array} \end{equation}
Muatan yang terlingkupi oleh permukaan Gauss, perlu dibagi dalam tiga rentang jarak terhadap origin yaitu $0 < r \le R_1$, $R_1 \le r \le R_2$, dan $r \le R_2$ dalam bentuk
\begin{equation}\label{eqn:enclosed-charge} q_{\rm enc} = \left\{ \begin{array}{cc} 0, & 0 < r \le R_1, \newline \displaystyle Q \left( \frac{r^3 - R_1^3}{R_2^3 - R_1^3} \right), & R_1 \le r \le R_2, \newline Q, & r \le R_2, \end{array} \right. \end{equation}
Dengan demikian saat menggunakan hukum Gauss dengan menerapkan Persamaan \eqref{eqn:electric-field-form}, \eqref{eqn:gaussian-surface}, dan \eqref{eqn:enclosed-charge} perlu dibagi dalam tiga rentang jarak terhadap origin. Untuk rentang $0 \le r \le R_1$
\begin{equation}\label{eqn:gauss-law-hollow-sphere-0-r-r1} \begin{array}{rcl} \displaystyle \oint \vec{E} \cdot d\vec{A} & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline \displaystyle \oint E(r) \ \hat{r} \cdot \hat{r} \ dA & = & \newline \displaystyle \oint E(r) dA & = & \newline \displaystyle \oint E(r) (r d\theta) (r \sin\theta d\phi) & = & \newline \displaystyle E(r) \ r^2 \oint \sin\theta d\theta d\phi & = & \newline \displaystyle E(r) \ r^2 \int_0^\pi \sin\theta d\theta \int_0^{2\pi} d\phi & = & \newline E(r) \ r^2 \ (2) \ (2\pi) & = & \displaystyle \frac{0}{\varepsilon_0} \newline E(r) & = & 0, \end{array} \end{equation}
dikarenakan tidak ada muatan yang terlingkupi oleh permukaan Gaussnya. Selanjutnya, untuk rentang $R_1 \le r \le R_2$ akan diperoleh
\begin{equation}\label{eqn:gauss-law-hollow-sphere-r1-r-r2} \begin{array}{rcl} \displaystyle \oint \vec{E} \cdot d\vec{A} & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline E(r) \ r^2 \ (2) \ (2\pi) & = & \displaystyle \frac{1}{\varepsilon_0} \left[ Q \frac{(r^3 - R_1^3)}{R_2^3 - R_1^3} \right] \newline E(r) & = & \displaystyle \frac{1}{4\pi r^2} \ \frac{1}{\varepsilon_0} \left( Q \frac{r^3 - R_1^3}{R_2^3 - R_1^3} \right) \newline & = & \displaystyle \frac{1}{4\pi\varepsilon_0} \left( \frac{r^3 - R_1^3}{R_2^3 - R_1^3} \right) \frac{Q}{r^2}. \end{array} \end{equation}
Dan untuk $r \le R_2$ akan memberikan
\begin{equation}\label{eqn:gauss-law-hollow-sphere-r2-r} \begin{array}{rcl} \displaystyle \oint \vec{E} \cdot d\vec{A} & = & \displaystyle \frac{q_{\rm enc}}{\varepsilon_0} \newline E(r) \ r^2 \ (2) \ (2\pi) & = & \displaystyle \frac{Q}{\varepsilon_0} \newline E(r) & = & \displaystyle \frac{1}{4\pi r^2} \ \frac{Q}{\varepsilon_0} \newline & = & \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{r^2}. \end{array} \end{equation}
Persamaan \eqref{eqn:gauss-law-hollow-sphere-0-r-r1}, \eqref{eqn:gauss-law-hollow-sphere-r1-r-r2}, dan \eqref{eqn:gauss-law-hollow-sphere-r2-r} dapat disarikan menjadi
\begin{equation}\label{eqn:gauss-law-hollow-sphere} E(r) = \left\{ \begin{array}{cc} 0, & 0 < r \le R_1, \newline \displaystyle \frac{1}{4\pi\varepsilon_0} \left( \frac{r^3 - R_1^3}{R_2^3 - R_1^3} \right) \frac{Q}{r^2}, & R_1 \le r \le R_2, \newline \displaystyle \frac{1}{4\pi\varepsilon_0} \ \frac{Q}{r^2}, & r \le R_2. \end{array} \right. \end{equation}
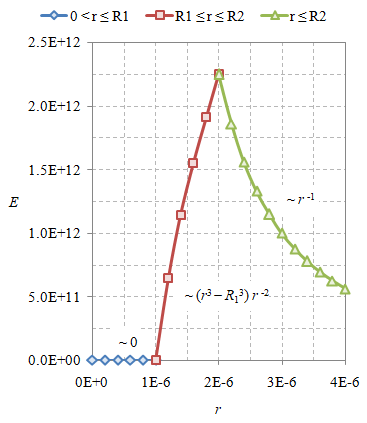
Gambar 2. Medan listrik $E$ sebagai fungsi jarak $r$ dari pusat origin untuk bola pejal berongga yang terbuat dari isolator bermuatan seragam.
Ilustrasi grafik medan listrik $E$ sebagai fungsi jarak dari origin $r$ diberikan pada Gambar 2 dengan $Q = 1 \ {\rm nC}$, $R_1 = 1 \ {\rm \mu m}$, dan $R_2 = 2 \ {\rm \mu m}$. Perhatikan bahwa bentuk kurva pada rentang $R_1 \le r \le R_2$ merupakan hasil perkalian antara suku $(r^3 - R_1^3)$ dan $r^{-2}$.
— Sparisoma Viridi (@6unpnp) January 30, 2022