linear programming

Pemrograman linier merupakan satu dari cara paling sederhana untuk melakukan optimasi, yang dapat membantu menyelesaikan masalah beberapa masalah amat rumit dengan membuat beberapa asumsi penyederhanaan [1], dan termasuk dalam teknik pemodelan matematika, dengan suatu fungsi linier dimaksimumkan atau diminimumkan saat dikenakan pada berbagai kendala, yang berguna sebagai panduan pengambilan keputusan secara kuantitatif dalam perencanaan bisnis, rekayasa industri, dan juga bidang sosial dan ilmu-ilmu fisika [2].

steps

Secara umum pemrograman linier atau linear programming (LP) mendefinsikan masalahnya secara generik dalam langkah-langkah [1]

1. Identifikasi variabel desisi,
2. Tuliskan fungsi obyektif,
3. Singgung kendala,
4. Nyatakan secara eksplisit pembatasan tidak-negatif.

Untuk LP semua variabel desisi, fungsi obyektif, dan kendala harus merupakan fungsi linier.

notation

Variabel desisi umumnya dinyatakan sebagai

\begin{equation}\label{eqn:decision-variable} x = [x_1, x_2, \dots, x_n] \in \mathbb{R}^n, \end{equation}

dengan $n$ menyatakan dimensi atau jumlah elemen dari $x$ yang merupakan bagian dari himpunan bilangan riil $\mathbb{R}$.

Fungsi obyektif $f: \mathbb{R}^n \mapsto \mathbb{R}$ memetakan $x \in \mathbb{R}^n$ menjadi $f(x) \in \mathbb{R}$ dalam bentuk

\begin{equation}\label{eqn:objective-function} f(x) = c^Tx = c_1 x_1 + c_2 x_2 + \dots + c_n x_n \end{equation}

dengan $c = [c_1, c_2, \dots, c_n]^T \in \mathbb{R}^n$ seperti halnya $x$.

Kendala dituliskan dalam bentuk pertidaksamaan

\begin{equation}\label{eqn:constraint} a_{j1} a_1 + a_{j2} x_2 + \dots + a_{jn} x_n \le b_j, \end{equation}

dengan $j = 1, 2, \dots, m$, bila terdapat $m$ buah kendala.

Solusi dicari dengan meminimukan Persamaan \eqref{eqn:objective-function} dengan kendala pada Persamaan \eqref{eqn:constraint}.

graphical method

Metode grafik digunakan untuk optimasi pemrograman linier dua-variabel, sehingga bila masalah memiliki dua variabel desisi, suatu metode grafik merupakan metode terbaik untuk menemukan solusi optimalnya [3]. Dikarenakan hanya terdapat dua variabel desisi maka masalah dapat digambarkan pada bidang $xy$. Himpunan pertidaksamaan merupakan kendala yang dilukiskan pada bidang $xy$, sehingga menghasilkan wilayah feasibel yang merupakan wilayah perpotongan yang dihasilkan. Solusi optimal terdapat pada wilayah ini, misalnya pada salah satu titik sudutnya atau verteks [4]. Hal ini dikarenakan hanya pada titik-titik batas tersebut, yang bukan terletak baik pada sumbu $x$ ataupun $y$, turunan fungsi obyektif memiliki solusi [5].

example 1

Bahan $x$ memiliki harga $4 {\rm / g}$ dan bahan $y$ memiliki harga $10 \ {\rm / g}$. Biaya produksi maksimal yang diijinkan adalah $36 {\rm}$ dan massa maksimal bahan adalah $6 \ {\rm g}$. Kekuatan bahan ditentukan dengan fungsi $f(x,y) = 3x + 4y$. Maksimalkan kekuatan bahan yang akan dibuat. Sebagai catatan, sebenarnya yang dicari adalah massa bahan $x$ dan massa bahan $y$, yang untuk penyederhaan digunakan saja simbol $x$ dan $y$ ketimbang $m_x$ dan $m_y$.

Langkah-langkah dapat dilakukan dengan hasil per langkahnya adalah sebagai berikut ini.

1. Fungsi obyektif: $f(x,y) = 3x + 4y$,
2. Kendala:
   • Biaya produksi (cost): $4x + 10y \le 36$,
   • Massa bahan (mass): $x + y \le 6$,
3. Batas-batas wilayah feasible:
   • $(6, 0)$,
   • $(4, 20)$,
   • $(0, 3.6)$,
   • $(0, 0)$,
4. Solusi optimum ($x \ge 0$ dan $y \ge 0$): $(4, 20)$.

Ilustrasi wilayah feasibel dan titik-titik batasnya diberikan pada gambar berikut ini.

Gambar 1. Wilayah feasible dan batas-batasnya serta nilai fungsi obyektif pada titik-titik batas tersebut.

Dengan demikian diperoleh bahwa mass bahan $x$ adalah $4 \ {\rm g}$ dan massa bahan $y$ adalah $2 \ {\rm g}$, yang akan memberikan kekuatan maksimum $f(4, 2) = 20$. Pembatasan tidak negatif ($x \ge 0$ dan $y \ge 0$) tidak dilukiskan pada Gambar 1 agar tidak menjadi terlalu kompleks. Gambar 1 dibuat dengan menggunakan GeoGebra yang versi daringnya dapat dilihat serta dimodifikasi di dvtnyfrb.

simplex method

Metode simpleks menggunakan pendekatan yang sangat efisien dengan tidak menghitung semua nilai fungsi obyektif akan tetapi mulai dari suatu titik sudut atau verteks dari wilayah feasibel, di mana semua variabel utama bernilai nol, dan secara sistematis berpindah dari satu titik sudut ke titik sudut lain sambil memperbaiki nilai fungsi obyektif pada setiap tahapnya [6], dengan langkah-langkahnya adalah seperti di bawah ini.

1. Persiapkan masalah dengan menuliskan fungsi obyektif dan semua pertidaksamaan kendala.
2. Ubah pertidaksamaan menjadi persamaan dengan menambahkan variabel slack pada setiap pertidaksamaan.
3. Bangun bagan (tableau) simpleks awal dengan menuliskan fungsi obyektif pada beris terbawah.
4. Tentukan kolom pivot yang teridentifikasi melalui entri bernilai paling negatif pada baris terbawah.
5. Hitung hasil-bagi (quotient) antara kolom paling kanan dengan kolom pivot, di mana hasil-bagi terkecil mengidentifikasikan suatu baris, yang irisannya dengan kolom pivot memberikan elemen pivot, dengan mengabaikan hasil-bagi yang nol, berharga negatif, atau tak-hingga.
6. Lakukan pivoting untuk membuat nol kolom ini yang dilakukan dengan cara yang sama pada metode Gauss-Jordan.
7. Selesai bila tidak ada lagi nilai negatif pada baris terbawah akan tetapi bila belum ulangi kembali langkah 4.
8. Baca hasilnya dengan mendapatkan variabel menggunakan kolom dengan 0 dan 1, di mana semua variabel berharga nol. Nilai maksimum muncul pada sudut kanan bawah.

Sebagai contoh akan digunakan kembali contoh sebelumnya, yang telah dipecahkan oleh metode grafik.

example 1

Deskripsi contoh tidak dituliskan kembali akan tetapi langsung ke penulisan langkah-langkahnya.

1. Fungsi obyektif dan pertidaksamaan kendala:
   • Fungsi obyektif: $f(x,y) = 3x + 4y$ menjadi $z = 3x_1 + 4x_2$,
   • Kendala biaya produksi: $4x + 10y \le 36$ menjadi $4x_1 + 10x_2 \le 36$,
   • Kendala massa bahan: $x + y \le 6$ menjadi $x_1 + x_2 \le 6$,
   • Nilai positif: $x \ge 0$; $y \ge 0$ menjadi $x_1 \ge 0$; $x_2 \ge 0$.
2. Penambahan variabel slack dan mengubah penulisan fungsi obyektif:
   • $-3x_1 - 4x_2 + z = 0$,
   • $4x_1 + 10x_2 + y_1 = 36$,
   • $x_1 + x_2 + y_2 = 6$,
   • $x_1 \ge 0$; $x_2 \ge 0$.
3. Bagan (tableau) inisial (dengan fungsi obyektif pada baris terbawah):
   
4. Cari kolom nilai paling negatif pada baris terbawah:
   Kolom pivot diberikan oleh kolom kedua dengan nilai $-4$ yang merupakan nilai palng negatif:
   
5. Hitung hasil-bagi kolom paling kanan dengan kolom pivot:
   
   Hasil-bagi minimum diberikan oleh baris pertama:
   
   Diperoleh elemen pivot adalah $10$.
6. Gunakan elemen pivot:
   • Bagi baris pivot dengan elemen pivot:
     
   • Buat nol kolom pivot kecuali nilai elemen pivot:
     
7. Periksa baris terbawah: Bila masih terdapat nilai negatif ulangi Langkah 4.

4. Cari kolom nilai paling negatif pada baris terbawah:
   
   Kolom pivot diberikan oleh kolom pertama dengan nilai $-1.4$ yang merupakan nilai palng negatif:
   
   
5. Hitung hasil-bagi kolom paling kanan dengan kolom pivot:
   
   Hasil-bagi minimum diberikan oleh baris kedua:
   
   Diperoleh elemen pivot adalah $0.6$.
6. Gunakan elemen pivot:
   • Bagi baris pivot dengan elemen pivot:
     
   • Buat nol kolom pivot kecuali nilai elemen pivot:
     
7. Periksa baris terbawah: Bila masih terdapat nilai negatif ulangi Langkah 4.
8. Baca hasilnya:
   

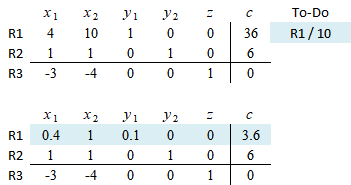
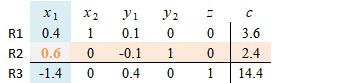
Dengan demikian diperoleh $x_1 = 4$ dan $x_2 = 2$, serta hasil fungsi obyektifnya $f(x_1, x_2) = 20$. Hasil ini cocok dengan yang diperoleh pada Gambar 1. Dapat pula dituliskan hasil pada langkah 8

\begin{equation}\label{eqn:solution} \left[ \begin{array}{cccc} x_1 & x_2 & z & c \newline 1 & 0 & 0 & 4 \newline 0 & 1 & 0 & 2 \newline 0 & 0 & 1 & 20 \end{array} \right] \end{equation}

yang merupakan solusinya. Perhatikan bahwa telah ditukar baris R1 dengan R2 agar menjadi bentuk echelon baris tereduksi.

exer

1. Di sepanjang garis yang menghubungkan titik $(0, 3.6)$ dan $(4, 2)$ pada Gambar 1 dapat diperoleh titik $(3, 2.4)$. Tunjukkan bahwa titik ini bukan merupakan solusi optimum.
2. Pada langkah ke delapan metode simpleks, apakah kolom untuk variabel slack perlu dinolkan?
3. Bagaimana batasan nilai variabel slack pada metode simpleks?

note

1. Karthe, “Introductory guide on Linear Programming for (aspiring) data scientists”, Analytics Vidhya, 28 Feb 2017, url https://www.analyticsvidhya.com/blog/2017/02/lintroductory-guide-on-linear-programming-explained-in-simple-english/ [20220208].
2. The Editors of Encyclopaedia Britannica, Yamini Chauhan, Erik Gregersen, “linear programming”, Encyclopaedia Britannica, 18 Jul 2017, url https://www.britannica.com/science/linear-programming-mathematics [20220208].
3. Aakash BYJU’S JEE, “Linear Programming”, BYJU’S, 23 Feb 2021, url https://byjus.com/maths/linear-programming/ [20220208].
4. Amir Ali Ahmadi, “Linear Programming”, Lec11p1, ORF 363 / COS 323 Computing and Optimization in the Physical and Social Sciences, Princeton University, Fall 2016, url https://www.princeton.edu/~aaa/Public/Teaching/ORF363_COS323/F16/ORF363_COS323_F16_Lec11.pdf [20220208].
5. cool, “Answer to ‘Why does the maximum/minimum of linear programming occurs at a vertex?’”, Math Stack Exchange, 13 Aug 2014, url https://math.stackexchange.com/a/896412/645927 [20220208].

comments

#bug0451

— Sparisoma Viridi (@6unpnp) February 8, 2022