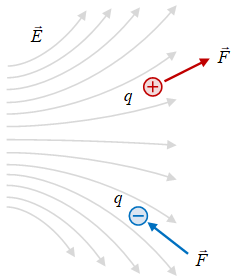
Gambar 1. Muatan titik $q$ yang berada dalam medan listrik $\vec{E}$ akan mengalami gaya listrik $\vec{F}$.
Hukum Coulomb memberikan rumusan gaya listrik yang bekerja pada suatu muatan titik akibat keberadaan muatan titik lain [1] dan dengan analogi gaya gravitasi konsep gaya listrik ini dapat diperluas sebagai interaksi antara muatan titik dengan medan [2].
Gaya listrik $\vec{F}$ yang bekerja pada muatan titik $q$ yang berada pada posisi $\vec{r}$ memiliki bentuk
\begin{equation}\label{eqn:electric-force} \vec{F} = q\vec{E}, \end{equation}
dengan $\vec{E}$ adalah medan listrik. Medan listrik $\vec{E}$ disebakan oleh muatan lain yang dapat berupa muatan titik, beberapa muatan titik, ataupun distribusi kontinu muatan.

Gambar 1. Muatan titik $q$ yang berada dalam medan listrik $\vec{E}$ akan mengalami gaya listrik $\vec{F}$.
Ilustrasi Persamaan \eqref{eqn:electric-force} diberikan pada Gambar 1, di mana untuk $q > 0$ arah $\vec{F}$ akan sama dengan arah $\vec{E}$ dan bila $q < 0$ maka arah $\vec{F}$ akan berlawanan dengan arah $\vec{E}$.
Medan listrik $\vec{E}$ dalam Persamaan \eqref{eqn:electric-force} dapat berbentuk
\begin{equation}\label{eqn:electric-field-point-charge} \vec{E} = \frac{1}{4\pi\varepsilon_0} \frac{q_1}{|\vec{r} - \vec{r}_1|^3} (\vec{r} - \vec{r}_1), \end{equation}
bila sumbernya merupakan muatan titik lain $q_1$ yang terletak di posisi $\vec{r}_1$. Substitusi Persamaan \eqref{eqn:electric-field-point-charge} ke Persamaan \eqref{eqn:electric-force} akan menghasilkan
\begin{equation}\label{eqn:coulomb-law-point-charge} \vec{F} = \frac{1}{4\pi\varepsilon_0} \frac{q q_1}{|\vec{r} - \vec{r}_1|^3} (\vec{r} - \vec{r}_1), \end{equation}
yang merupakan hukum Coulomb, dengan ilustrasinya diberikan pada gambar berikut ini.
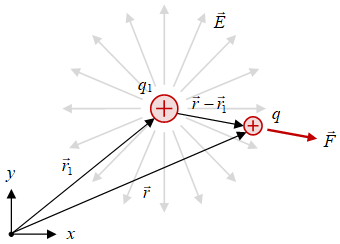
Gambar 2. Muatan titik $q$ pada posisi $\vec{r}$ yang berada dalam medan listrik $\vec{E}$, yang disebabkan oleh muatan titik lain $q_1$ pada posisi $\vec{r}_1$, akan mengalami gaya listrik $\vec{F}$.
Persamaan \eqref{eqn:coulomb-law-point-charge} dibaca sebagai gaya elektrostatik atau gaya listrik pada muatan $q$ yang berada pada posisi $\vec{r}$ akibat adanya muatan sumber $q_1$ yang berada pada posisi $\vec{r}_1$. Gambar 2 memberikan ilustrasi mengenai gaya listrik pada muatan $q$ tersebut.
Bila terdapat banyak muatan titik $q_i$, $i = 1, 2, \dots, N$ yang terletak masing-masing pada posisi $\vec{r}_i$, Persamaan \eqref{eqn:coulomb-law-point-charge} akan menjadi
\begin{equation}\label{eqn:coulomb-law-some-point-charges} \vec{F} = \sum_{i =1}^N \frac{1}{4\pi\varepsilon_0} \frac{q q_1}{|\vec{r} - \vec{r}_1|^3} (\vec{r} - \vec{r}_1), \end{equation}
dengan syarat bahwa $\left| \vec{r} - \vec{r}_i \right| \ne 0$, yang berarti bahwa titik tempat muatan $q$ berada tidak boleh pada salah satu muatan sumber medan listriknya.
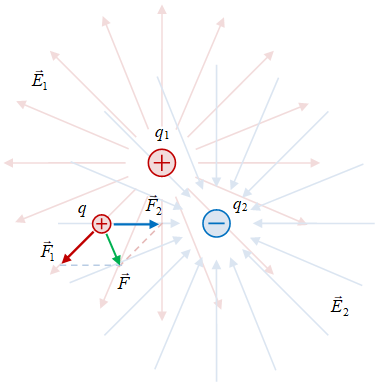
Gambar 3. Muatan titik $q$ pada posisi $\vec{r}$ yang berada dalam medan listrik $\vec{E}$, yang disebabkan oleh beberapa muatan titik lain $q_i$ pada posisi $\vec{r}_i$ dengan $i = 1, 2, \dots, N$, akan mengalami gaya listrik $\vec{F}$, dengan dibatasi $N = 2$ agar tidak terlalu rumit penggambarannya.
Gaya listrik $\vec{F}$ pada muatan $q$ pada posisi $\vec{r}$ akibat medan listrik $\vec{E}$ yang disebabkan oleh semua muatan $q_i$ dengan $i = 1, 2, \dots, N$, merupakan penjumlahan secara vektor dari gaya listrik $\vec{F}_i$ pada muatan $q$ akibat medan listrik $\vec{E}_i$ dari masing-masing muatan $q_i$. Ilustrasi hal ini diberikan pada Gambar 3.
Sebuah cakram dengan jari-jari $R$ dan berapat muatan seragam $\sigma$ yang terletak pada bidang $y = y_0$ dan pusat cakram dilewati sumbu $y$ akan memberikan medan listrik
\begin{equation}\label{eqn:electric-field-disc} \vec{E} = \hat{y} \frac{\sigma}{2\varepsilon_0} \left( \frac{y - y_0}{|y - y_0|} - \frac{y - y_0}{ \sqrt{(y - y_0)^2 + R^2}} \right) \end{equation}
yang bila diterapkan pada Persamaan \eqref{eqn:electric-force} untuk muatan yang terletak di sepanjang sumbu $y$ akan memberikan
\begin{equation}\label{eqn:coulomb-law-disc} \vec{F} = \hat{y} \frac{q\sigma}{2\varepsilon_0} \left( \frac{y - y_0}{|y - y_0|} - \frac{y - y_0}{ \sqrt{(y - y_0)^2 + R^2}} \right) \end{equation}
sebagai gaya listriknya.
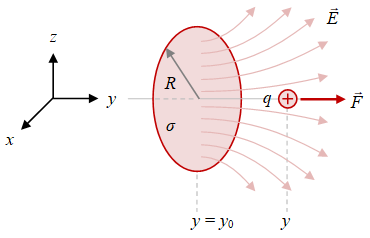
Gambar 4. Muatan titik $q$ di sepanjang sumbu $y$ mengalami gaya listrik $\vec{F}$ akibat cakram berjari-jari $R$ dan berapat muatan seragam $\sigma$ yang terletak pada bidang $y = y_0$.
Ilustrasi untuk Persamaan \eqref{eqn:coulomb-law-disc} diberikan pada Gambar 4, yang berlaku hanya bagi muatan yang terletak di sepanjang sumbu $y$. Bila muatan tidak terletak di sepanjang sumbu $y$, medan listriknya tidak lagi mematuhi Persamaan \eqref{eqn:electric-field-disc}.
Dengan memilih $R \rightarrow \infty$ sehingga cakram dapat menjadi suatu pelat amat luas, Persamaan \eqref{eqn:coulomb-law-disc} akan menjadi
\begin{equation}\label{eqn:coulomb-law-disc-large} \vec{F} = \hat{y} \frac{q\sigma}{2\varepsilon_0} \frac{y - y_0}{|y - y_0|}, \end{equation}
yang dapat pula dituliskan sebagai
\begin{equation}\label{eqn:coulomb-law-disc-large-y0} \vec{F} = \left\{ \begin{array}{rcl} \displaystyle -\hat{y} \frac{q\sigma}{2\varepsilon_0}, & y < y_0 \newline \displaystyle \hat{y} \frac{q\sigma}{2\varepsilon_0}, & y_0 < y, \end{array} \right. \end{equation}
sehingga lebih jelas bahwa medan listrik ke arah kiri di sebelah kiri pelat dan ke arah kanan di sebelah kanan pelat. Pada kedua daerah tersebut terdapat konsistensi bahwa medan listrik keluar dari pelat untuk rapat muatan bertanda positif, $\sigma > 0$.
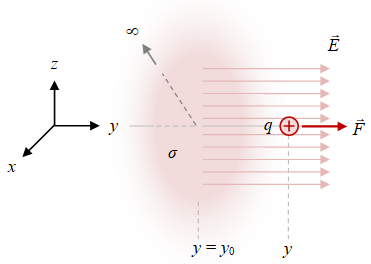
Gambar 5 Muatan titik $q$ di dekat sebuah pelat luas berapat muatan seragam $\sigma$ yang terletak pada bidang $y = y_0$ akan mengalami medan listrik $\vec{F}$.
Untuk suatu pelat luas bermuatan seragam $\sigma$ medan listriknya $\vec{E}$ dapat dianggap bernilai tetap pada daerah di dekat pelat sehingga posisi muatan $q$ yang ingin dihitung gaya listriknya $\vec{F}$ dapat cukup bebas sebagaimana diberikan pada Gambar 5, tidak lagi perlu harus di sepanjang suatu sumbu seperti pada kasus sebelumnya dalam Gambar 4.
Suatu muatan berbentuk garis dengan rapat muatan seragam $\lambda$ yang terletak pada sumbu $z$ dari $z = -L_1$ sampai $z = L_2$ akan memberikan medan listrik di sepanjang sumbu $y$ pada jarak $H$ dalam bentuk
\begin{equation}\label{eqn:electric-field-line-of-charge} \begin{array}{rcl} \vec{E} & = & \displaystyle k\frac{\lambda}{H} \left( \frac{H}{\sqrt{H^2 + (L_2)^2}} - \frac{H}{\sqrt{H^2 + (-L_1)^2}} \right) \hat{z} \newline & & + \displaystyle k\frac{\lambda}{H} \left[ \frac{(L_2)}{\sqrt{H^2 + (L_2)^2}} - \frac{(-L_1)}{\sqrt{H^2 + (-L_1)^2}} \right] \hat{y} \newline \end{array} \end{equation}
sehingga
\begin{equation}\label{eqn:electric-force-line-of-charge} \begin{array}{rcl} \vec{F} & = & \displaystyle k\frac{q \lambda}{H} \left( \frac{H}{\sqrt{H^2 + (L_2)^2}} - \frac{H}{\sqrt{H^2 + (-L_1)^2}} \right) \hat{z} \newline & & + \displaystyle k\frac{q \lambda}{H} \left[ \frac{(L_2)}{\sqrt{H^2 + (L_2)^2}} - \frac{(-L_1)}{\sqrt{H^2 + (-L_1)^2}} \right] \hat{y} \newline \end{array} \end{equation}
adalah gaya $\vec{F}$ yang dialami oleh titik muatan $q$ di sepanjang sumbu $y$, yang diperoleh menggunakan Pesamaan \eqref{eqn:electric-force}.
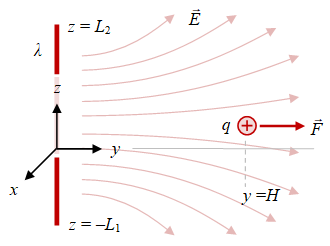
Gambar 6. Muatan $q$ yang terletak di sepanjang sumbu $y$ mengalami gaya listrik $\vec{F}$ akibat distribusi muatan garis yang terletak pada sumbu $z$.
Sebuah muatan berbentuk distribusi muatan garis dengan rapat muatan seragam $\lambda$ yang terletak pada sumbu $z$ memberikan medan listrik pada muatan $q$ yang terletak di sepanjang sumbu $z$ pada jarak $H$ dari muatan garis, dengan rumusannya diberikan oleh Persamaan \eqref{eqn:electric-force-line-of-charge} dan ilustrasinya terdapat pada Gambar 5.
Untuk suatu kawat lurus dengan panjang tak-hingga, $L_1 \rightarrow \infty$ dan $L_2 \rightarrow \infty$, Persamaan \eqref{eqn:electric-force-line-of-charge} akan menjadi
\begin{equation}\label{eqn:electric-force-line-of-charge-infinite-wire} \vec{F} = k\frac{q 2\lambda}{H} \hat{y}. \end{equation}
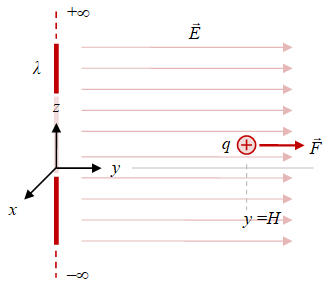
Gambar 7. Muatan garis dengan panjang tak-hingg memberikan gaya listrik pada muatan $q$ yang berjarak $H$ darinya.
Muatan garis memiliki panjang tak-hingga akan menyebabkan medan lisrik $\vec{E}$ di sekitarnya memiliki arah yang selalu tegak lurus panjang muatan garis, dengan ilustrasinya diberikan pada Gambar 6 dan perumusannya pada Persamaan \eqref{eqn:electric-force-line-of-charge-infinite-wire}.
Untuk muatan berbentuk bola, baik bola pejal berbahan konduktor ataupun isolator, kulit bola, bola berongga, dan variasi lainnya medan listrik di luar bola selalu berbentuk
\begin{equation}\label{eqn:electric-field-spherical-system} \vec{E} = \frac{1}{4\pi\varepsilon_0} \frac{q_1}{r^2} \hat{r}, \end{equation}
dengan $q_1$ merupakan muatan total sistem berbentuk bola tersebut. Di sini telah diambil pusat koordinat terletak pada pusat bola untuk penyederhanaan formulasinya.
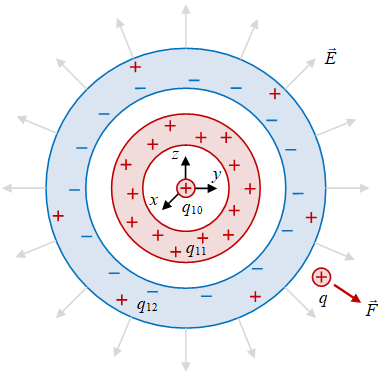
Gambar 8. Muatan berbentuk bola dengan muatan titik ditengah bola isolator berongga dalam bola konduktor berongga memberikan medan listrik $\vec{E}$ di sekelilingnya sehingga titik muatan $q$ yang berada pada posisi $\vec{r}$ dari pusat bola akan mengalami gaya listrik $\vec{F}$.
Gaya listrik $\vec{F}$ yang dialami oleh muatan titik $q$ pada posisi $\vec{r}$ dari pusat bola dengan susunan dalamnya seperti Gambar 7 mirip seperti kasus pada satu titik muatan. Perbedaannya adalah $q_1$ bukan sekedar muatan titik akan tetapi jumlah total muatan sistem muatan berbentuk bola yang, misalnya
\begin{equation}\label{eqn:spherical-system-charge} q_1 = q_{10} + q_{11} + q_{12}, \end{equation}
untuk sistem pada Gambar 7, dengan $q_{10}$ adalah muatan titik muatan, $q_{11}$ adalah muatan bola berongga isolator, dan $q_{12}$ adalah muatan bola berongga konduktor.
— Sparisoma Viridi (@6unpnp) February 12, 2022