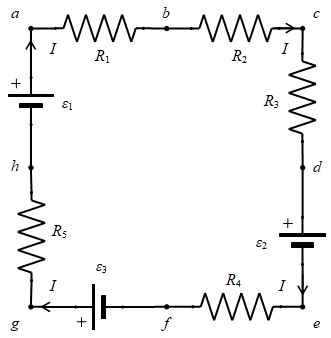
Gambar 1. Rangkaian arus searah dengan tiga buah baterai $\varepsilon_1$, $\varepsilon_2$, $\varepsilon_3$ dan lima resistor $R_1$, $R_2$, $R_3$, $R_4$, $R_5$, yang ketujuh komponen tersebut tersusun secara seri.
Dengan mengikuti arah arus listrik yang melewati suatu resistor, yang mengalir dari kaki resistor dengan potensial listrik lebih tinggi ke kaki lain dengan potensial listrik lebih rendah, akan diperoleh penurunan tegangan [1]. Istilah tegangan dalam sebuah baterai mengacu pada perbedaan potensial listrik antara terminal positif dan negatif baterai [2], yang bagaimana hal ini dapat terjadi telah dijelaskan dengan model sederhana baterai [3].
Terdapat beberapa konvensi yang digunakan di sini, yaitu
Sebagai contoh bila arus $I$ mengalir dari titik $a$ ke titik $b$ melalui sebuah resistor $R$ maka penurunan tegangannya adalah $IR$ atau $V_{ab} = V_a - V_b = IR$. Perhatikan bahwa $V_a > V_b$ karena arus mengalir dari titik dengan potensial listrik lebih tinggi ke titik dengan potensial listrik lebih rendah.
Untuk sebuah baterai $\varepsilon$ bila terminal positif tertaut dengan titik $a$ dan terminal negatif tertaut dengan titik $b$ maka $V_{ab} = V_a - V_b = \varepsilon$ karena saat dihubungkan dengan suatu kawat arus akan mengalir dari titik $a$ ke $b$ melalui kawat yang berarti $V_a > V_b$.
Suatu rangkaian DC yang terdiri dari tiga baterai dan lima resistor adalah seperti di bawah ini.

Gambar 1. Rangkaian arus searah dengan tiga buah baterai $\varepsilon_1$, $\varepsilon_2$, $\varepsilon_3$ dan lima resistor $R_1$, $R_2$, $R_3$, $R_4$, $R_5$, yang ketujuh komponen tersebut tersusun secara seri.
Konvensi 1 telah dicantumkan pada Gambar 1 sehingga penelusuran beda potensial akan mengikuti urutan titik-titik $a$ $\rightarrow$ $b$ $\rightarrow$ $c$ $\rightarrow$ $d$ $\rightarrow$ $e$ $\rightarrow$ $f$ $\rightarrow$ $g$ $\rightarrow$ $h$ $\rightarrow$ $a$ sebagai implementasi Konvensi 2.
Tabel 1. Tegangan antara dua titik $i$ (inisial, awal) dan $f$ (final, akhir) mengikuti arah arus.
| $i$ | $f$ | $v_{if}$ |
|---|---|---|
| $a$ | $b$ | $I R_1$ |
| $b$ | $c$ | $I R_2$ |
| $c$ | $d$ | $I R_3$ |
| $d$ | $e$ | $\varepsilon_2$ |
| $e$ | $f$ | $I R_4$ |
| $f$ | $g$ | $-\varepsilon_3$ |
| $g$ | $h$ | $I R_5$ |
| $h$ | $a$ | $-\varepsilon_1$ |
Isi pada Tabel 1 merupakan implementasi Konvensi 3 untuk resistor dan Konvesi $4$ untuk baterai. Kolom terakhir pada tabel merupakan penerapan Konvensi 5. Selanjutnya dapat dituliskan bahwa
\begin{equation}\label{eqn:voltage-in-a-loop} \begin{array}{c} V_{ab} + V_{bc} + V_{cd} + V_{de} + V_{ef} \newline + V_{fg} + V_{gh} + V_{ha} = 0, \end{array} \end{equation}
yang dengan menggunakan informasi dari Tabel 1 akan memberikan
\begin{equation}\label{eqn:kirchhoff-law-2} \begin{array}{c} I R_1 + I R_2 + I R_3 + \varepsilon_2 + I R_4 \newline - \varepsilon_3 + I R_5 - \varepsilon_1 = 0 \end{array} \end{equation}
yang tak lain merupakan hukum II Kirchhoff. Dari Persamaan \eqref{eqn:kirchhoff-law-2} dapat diperoleh
\begin{equation}\label{eqn:kirchhoff-law-2-current} I = \frac{\varepsilon_1 - \varepsilon_2 + \varepsilon_3}{R_1 + R_2 + R_3 + R_4 + R_5} \end{equation}
yang merupakan arus yang mengaliri simpul pada Gambar 1.
Nilai-nilai baterai $\varepsilon_1$, $\varepsilon_2$, $\varepsilon_3$ dan resistor $R_1$, $R_2$, $R_3$, $R_4$, $R_5$ diberikan pada gambar berikut ini.

Gambar 2. Sebuah simpul dengan $\varepsilon_1 = 9 \ {\rm V}$, $\varepsilon_1 = 1.5 \ {\rm V}$, $\varepsilon_3 = 7.5 \ {\rm V}$ dan $R_1 = 1 \ \Omega$, $R_2 = 2 \ \Omega$, $R_3 = 3 \ \Omega$, $R_4 = 4 \ \Omega$, $R_5 = 5 \ \Omega$.
Dengan informasi dari Gambar 2 dan Persaamaan \eqref {eqn:kirchhoff-law-2-current} akan diperoleh arus yang mengalir pada simpul
\[\begin{array}{rcl} I & = & \displaystyle \frac{9 - 1.5 + 7.5}{1 + 2 + 3 + 4 + 5} \newline & = & \displaystyle \frac{15}{15} \newline & = & 1 \ {\rm A}. \end{array}\]Dengan hasil arus ini Tabel 1 dapat dilengkapi menjadi
Tabel 2. Tegangan antara dua titik $i$ (inisial, awal) dan $f$ (final, akhir) setelah arus $I$ diketahui nilainya.
| $i$ | $f$ | $v_{if}$ (V) |
|---|---|---|
| $a$ | $b$ | $1$ |
| $b$ | $c$ | $2$ |
| $c$ | $d$ | $3$ |
| $d$ | $e$ | $1.5$ |
| $e$ | $f$ | $4$ |
| $f$ | $g$ | $-7.5$ |
| $g$ | $h$ | $5$ |
| $h$ | $a$ | $-9$ |
Tabel 2 hanya menunjukkan beda potensial antar dua titik dan belum potensial berdasarkan suatu titi referensi.
Suatu titik referensi dapat dipilih dan ditetapkan nilai potensial listriknya sehingga titik-titik lain potensialnya akan dinyatakan secara relatif terhadap titik tersebut.

Gambar 3. Potensial listrik di setiap titik dengan referensi $V_g = 0 \ {\rm V}$.
Titik $g$ dipilih sebagai referensi dan ditetapkan nilai potensialnya adalah nol yang ditunjukkan dengan simbol pembumian atau ground berupa ⏚. Lalu bagaimana cara memperoleh potensial di setiap titik dengan hanya mengetaui bahwa $V_g = 0 \ {\rm V}$? Gunakan Konvensi 5 dan informasi pada Tabel 2. Untuk titik $f$
\[\begin{array}{rcl} V_f - V_g & = & V_{fg} \newline V_f & = & V_{fg} + V_g \newline & = & -7.5 + 0 \newline & = & -7.5 \ {\rm V} \end{array}\]dan titik $h$
\[\begin{array}{rcl} V_{gh} & = & V_g - V_h \newline V_h & = & V_g - V_{gh} \newline & = & 0 - 5 \newline & = & -5 \ {\rm V}, \end{array}\]yang memberikan hasil seperti pada Gambar 3.
Nilai potensial referensi bebas ditetapkan dan titik yang dijadikan referensi juga bebas. Dengan tetap menggunakan titik $g$ akan tetapi saat ini diberi nilai potensial berbeda, yaitu $4 \ {\rm V}$, gambar simpulnya akan menjadi seperti berikut ini.

Gambar 4. Simpul dengan $V_g = 4 \ {\rm V}$.
Kembali gunakan Konvensi 5, informasi pada Tabel 2, dan ditambah Gambar 4 untuk nilai $V_g$. Untuk titik $f$
\[\begin{array}{rcl} V_f - V_g & = & V_{fg} \newline V_f & = & V_{fg} + V_g \newline & = & -7.5 + 4 \newline & = & -3.5 \ {\rm V} \end{array}\]dan titik $h$
\[\begin{array}{rcl} V_{gh} & = & V_g - V_h \newline V_h & = & V_g - V_{gh} \newline & = & 4 - 5 \newline & = & -1 \ {\rm V}. \end{array}\]Dengan demikian dapat dihitung potensial pada titik $f$ dan $h$
— Sparisoma Viridi (@6unpnp) March 4, 2022