polynomial interpolation

Fungsi polinomial memiliki banyak kegunaan di dalam matematika, yang salah satunya adalah pada interpolasi [1]. Dua formula eksplisit interpolasi polinomial yang umum digunakan adalah polinomial Lagrange dan Newton [2], yang bersama-sama dengan spline dimanfaatkan dalam sains data [3]. Polinomial Lagrange telah pula diimplementasikan dalam bahasa Wolfram [4].

a polynomial function

Sebagai ilustrasi terdapat empat titik data dan satu titik yang ingin diperoleh melalui interpolasi polinomial sebagaimana diberikan pada gambar berikut ini.

Gambar 1. Hubungan titik-titik data $(x_1, y_1)$, $(x_2, y_2)$, $(x_3, y_3)$, dan $(x_4, y_4)$ dengan nilai yang ingin diperoleh $y$ bila diketahui $x$.

Perhatikan bahwa titik data $x$ yang ingin diketahui nilai fungsinya $y$ berada di atas semua nilai-nilai $y_1$, $y_2$, $y_3$, dan $y_4$. Orde suatu polinomial merupakan pangkat tertinggi dari suku-sukunya

\begin{equation}\label{eqn:polynomial-function-order-n} p(x) = \sum_{n = 0}^N c_n x^n, \end{equation}

di mana $N$ adalah orde polinomial. Perhatikan bahwa

adalah contoh polionomial berorde 4 walaupun terdapat suku-suku berorde rendah yang tidak ada dikarenakan $c_2 = 0$ dan $c_3 = 0$.

lagrange polynomial

Polinomial interpolasi Lagrange dengan derajat $\le (N-1)$ akan melewati $N$ buat titik-titik data $(x_1, y_1)$, .., $(x_N, y_N)$, di mana $y_i = f(x_i)$ dengan $f(x)$ adalah fungsi interpolasi yang akan dicari. Polinomial interpolasi Lagrange dirumuskan sebagai

\begin{equation}\label{eqn:lagrange-interpolating-polynomial-p} P(x) = \sum_{i = 1}^N P_i(x), \end{equation}

dengan

\begin{equation}\label{eqn:lagrange-interpolating-polynomial-pj} P_i(x) = y_i \prod_{\begin{array}{c}j = 1 \newline j \ne i \end{array}}^N \frac{x - x_j}{x_i - x_j}. \end{equation}

example

Terdapat data beberapa titik seperti diberikan pada gambar berikut ini.

Gambar 2. Titik-titik data $(1, 11)$, $(4, 18)$, $(7, 7)$, dan $(10, 5)$.

Akan dilakukan interpolasi polinomial pada empat titik data yang diberikan pada Gambar 2 sehingga dapat dicari nilai $y$ pada sembarang $x$ untuk $1 \le x \le 10$.

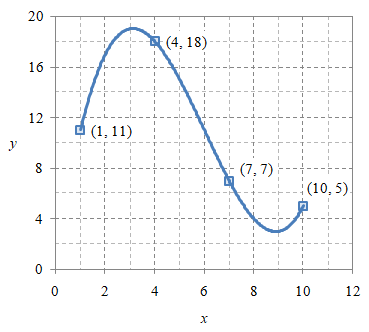
Gambar 3. Kurva hasil interpolasi polinomial untuk titik-titik data $(1, 11)$, $(4, 18)$, $(7, 7)$, dan $(10, 5)$.

Hasil interpolasi polinomial berupa kurva yang melewati semua titik-titik data diberikan pada Gambar 3.

code

Terdapat program sederhana menggunakan bahasa pemrograman Python berikut ini

# 0502-lagrange-inter.py
# Lagrange interpolatio
# Sparisoma Viridi | https://github.com/dudung
# 20220222 Create this example.

# define data points
x = [1, 4, 7, 10]
y = [11, 18, 7, 5]
N = min(len(x), len(y))


# define lagrange interpolating polynomial function p(x)
def prod(i, xx):
  prod = 1
  for j in range(N):
    if j != i:
      prodj = (xx - x[j]) / (x[i] - x[j])
    else:
      prodj = 1
    prod = prod * prodj

  return prod

def p(xx):
  sum = 0
  for i in range(N):
    pi = y[i] * prod(i, xx)
    sum = sum + pi
  
  return sum

# use the function
for xx in range(1, 11):
  yy = p(xx)
  print(xx, "%.3f" % yy)

yang akan memberikan hasil berikut

==== RESTART: 0502-lagrange-inter.py ====
1 11.000
2 17.000
3 19.000
4 18.000
5 15.000
6 11.000
7 7.000
8 4.000
9 3.000
10 5.000

saat dijalankan. Program tersebut dapat dijalan secara daring di OneCompiler 3xu45zkbs.

results

Hasil keluaran program dapat disajikan dalam bentuk tabel berikut ini.

Tabel 1 Hasil keluaran program ``.

Perhatikan bahwa nilai-nilai telah dibulatkan sampai dua angka di belakang koma pada Tabel 1 untuk yang bukan bilangan bulat. Nilai-nilai berwarna ($\color{#88e}\blacksquare$) adalah titik-titik data, sedangkan yang lainnnya merupakan hasil interpolasi polinomial

Gambar 4. Kurva interpolasi polinomial Lagrange dan titik-titik hasil interpolasi ($\circ$) serta titik-titik datanya semula ($\color{#88e}\blacksquare$).

Perhatikan bahwa pada Gambar 4 telah terdapat titik-titik pada kurva polinomial, yang semula hanya menghubungkan titik-titik data pada Gambar 3 dan belum ada titik-titik lain di antara titik-titik data.

exer

1. Dengan menggunakan program 0502-lagrange-inter.py carilah nilai $y$ untuk $x = 3.5, 6.5, 9.5$. Tampilkan sampai tiga angka di belakang koma.
2. Bagaimana dengan cepat mencari nilai-nilai yang diminta pada soal sebelumnya tanpa melakukan kompilasi programnya?

note

1. Arnab Chakraborty, “Polynomial interpolation”, Numerical Analysis (B-I, 2020), 27 Feb 2020, url https://www.isical.ac.in/~arnabc/numana/interpol1.html [20220222].
2. Wikipedia contributors, “Polynomial interpolation”, Wikipedia, The Free Encyclopedia, 26 January 2022, 11:29 UTC, url https://en.wikipedia.org/w/index.php?oldid=1068051549 [20220222].
3. Joos Korstanje, “Polynomial Interpolation”, Towards Data Science, 22 Jun 2021, url https://towardsdatascience.com/polynomial-interpolation-3463ea4b63dd [20220222].
4. Branden Archer, Eric W. Weisstein, “Lagrange Interpolating Polynomial”, from MathWorld–A Wolfram Web Resource, Wolfram Research, Inc., url https://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html [20220222].

comments

#bug0502

— Sparisoma Viridi (@6unpnp) February 22, 2022