
Gambar 1. Elemen medan magnetik $d\vec{B}$ yang disebabkan oleh elemen arus $Id\vec{l}$ terlihat dengan perspektif dan tampak atas, depan, bawah.
Medan magnetik oleh kawat lurus berarus dapat diperoleh dengan menggunakan hukum Biot-Savart [1] dan bila kawatnya amat panjang dapat menggunakan hukum Ampere [2]. Perihal medan magnetik oleh kawat lurus berarus dengan panjang berhingga masih menjadi pembahasan yang menarik, seperti bila ingin menerapkan hukum Ampere dengan perumusan yang lebih umum [3] dan pemanfaatannya untuk menghitung berbagai bentuk simpul arus [4].
Elemen arus listrik yang mengalir pada sebuah kawat $Id\vec{l}$ akan memberikan elemen medan magnetik $d\vec{B}$ pada posisi $\vec{r}$ dari kawat yang diberikan oleh hukum Biot-Savart
\begin{equation}\label{eqn:biot-savart-law} d\vec{B} = \frac{\mu_0}{4\pi} \frac{Id\vec{l} \times \vec{r}}{r^3}, \end{equation}
seperti digambarkan berikut ini.

Gambar 1. Elemen medan magnetik $d\vec{B}$ yang disebabkan oleh elemen arus $Id\vec{l}$ terlihat dengan perspektif dan tampak atas, depan, bawah.
Pusat koordinat dipilih berada pada kawat dan sumbu $z$ sejajar pada kawat sehingga dapat digunakan sistem koordinat silinder $(r, \theta, z)$ sebagaimana disajikan pada Gambar 1.
Di sini akan diterapkan hukum Biot-Savart untuk kawat lurus dengan panjang berhingga, salah satu ujung tak-hingga, dan kedua ujung tak-hingga.
Agar hukum Biot-Savart dapat diterapkan dengan mudah Gambar 1 perlu diperjelas dengan menambahkan batas-batas integral untuk $dl$ seperti pada gambar berikut ini.

Gambar 2. Elemen medan magnetik $d\vec{B}$ pada posisi $\vec{r}$ dari kawat yang disebabkan oleh elemen arus $Id\vec{l}$ tampak depan dan batas-batas integralnya.
Dari Gambar 2 dapat diperoleh
\begin{equation}\label{eqn:tan-theta-1} \tan \theta_1 = \frac{h}{-z_1} \end{equation}
dan
\begin{equation}\label{eqn:tan-theta-2} \tan \theta_2 = \frac{h}{-z_2} \end{equation}
dengan batas bawah integral adalah $z = -z_1$ dan batas atas integral adalah $z = -z_2$. Dapat pula dituliskan
\begin{equation}\label{eqn:cot-theta} \cot \theta = \frac{z}{h} \end{equation}
sehingga
\begin{equation}\label{eqn:cot-theta-z} z = h \cot \theta \end{equation}
dan diferensialnya
\begin{equation}\label{eqn:ctg-theta-dz} dz = -h \csc^2 \theta d\theta. \end{equation}
Vektor posisi relatif titik pengamatan terhadap elemen arus diperoleh dari Gambar 2
\begin{equation}\label{eqn:r-rel} \vec{r} = h \vec{r} + z \hat{z}, \end{equation}
sehingga besarnya adalah
\begin{equation}\label{eqn:r-rel-mag} r = \sqrt{h^2 + z^2}. \end{equation}
Substitusi Persamaan \eqref{eqn:cot-theta-z} ke Persamaan \eqref{eqn:r-rel-mag} akan memberikan
\begin{equation}\label{eqn:r-rel-mag-csc} r = h\csc \theta. \end{equation}
Dan
\begin{equation}\label{eqn:idl} Id\vec{l} = Idz\hat{z} \end{equation}
adalah elemen arus pada Gambar 2. Substitusi Persamaan \eqref{eqn:r-rel}, \eqref{eqn:r-rel-mag-csc}, dan \eqref{eqn:idl} ke Persamaan \eqref{eqn:biot-savart-law} akan menghasilkan
\begin{equation}\label{eqn:biot-savart-law-straight-wire} \begin{array}{rcl} d\vec{B} & = & \displaystyle \frac{\mu_0}{4\pi} \frac{Idz\hat{z} \times (h \vec{r} + z \hat{z})}{(h\csc \theta)^3} \newline & = & \displaystyle \hat{\theta} \frac{\mu_0}{4\pi} \frac{h I}{h^3\csc^3 \theta} \ dz \newline & = & \displaystyle \hat{\theta} \frac{\mu_0}{4\pi} \frac{h I}{h^3\csc^3 \theta} \ (-h \csc^2 \theta d\theta) \newline & = & \displaystyle -\hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} \frac{d\theta}{\csc\theta} \newline & = & \displaystyle -\hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} \sin\theta d\theta. \end{array} \end{equation}
Integral Persamaan \eqref{eqn:biot-savart-law-straight-wire} akan memberikan
\begin{equation}\label{eqn:biot-savart-law-straight-wire-b} \begin{array}{rcl} \vec{B} & = & \int d\vec{B} \newline & = & \displaystyle -\hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} \int \sin\theta d\theta \newline & = & \displaystyle -\hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} (-\cos\theta) \newline & = & \displaystyle \hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} \cos\theta. \end{array} \end{equation}
Dari Persamaan \eqref{eqn:cot-theta-z} dapat diperoleh
\begin{equation}\label{eqn:cos-theta-z} \cos \theta = \frac{z}{\sqrt{z^2 + h^2}}. \end{equation}
Dengan bantuan Persamaan \eqref{eqn:cos-theta-z} maka Persamaan \eqref{eqn:biot-savart-law-straight-wire-b} dapat menjadi
\begin{equation}\label{eqn:biot-savart-law-straight-wire-b-with-bounds} \vec{B} = \hat{\theta} \frac{\mu_0}{4\pi} \frac{I}{h} \left( \frac{z_2}{\sqrt{z_2^2 + h^2}} - \frac{z_1}{\sqrt{z_1^2 + h^2}} \right), \end{equation}
yang perlu memperhatikan nilai batas bawah dan batas atas $z$ pada kawat berarus $I$ penyebab medan magnetik $\vec{B}$. Tanda positif dan negatif perlu dimasukkan. Gambar 2 menunjukkan batas bawah integral adalah $z = -z_1$ dan batas atasnya adalah $z = -z_2$.
Dengan menggunakan Persamaan \eqref{eqn:biot-savart-law-straight-wire-b-with-bounds} dapat diperoleh untuk kawat berhingga, semi tak-hingga, dan tak hingga pada kedua ujungnya.
Terdapat beberapa kasus yang dapat disinggung terkait dengan pemanfaatan Persamaan \eqref{eqn:biot-savart-law-straight-wire-b-with-bounds} seperti diberikan pada tabel di bawah ini.
Tabel 1. Beberapa sistem kawat lurus berarus dan medan magnetik yang disebabkannya.
| No | Kasus | $B$ |
|---|---|---|
| 1 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ \frac{-l}{\sqrt{l^2 + h^2}} - \frac{-(l+L)}{\sqrt{(l+L)^2 + h^2}} \right]$ |
| 2 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left( \frac{L+l}{\sqrt{(L+l)^2 + h^2}} - \frac{l}{\sqrt{l^2 + h^2}} \right)$ |
| 3 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ \frac{l}{\sqrt{l^2 + h^2}} - \frac{-(L-l)}{\sqrt{(L-l)^2 + h^2}} \right]$ |
| 4 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ \frac{L-l}{\sqrt{(L-l)^2 + h^2}} - \frac{(-l)}{\sqrt{l^2 + h^2}} \right]$ |
| 5 | 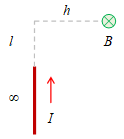 |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ \frac{-l}{\sqrt{l^2 + h^2}} - (-1) \right]$ |
| 6 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left( 1 - \frac{l}{\sqrt{l^2 + h^2}} \right)$ |
| 7 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ \frac{l}{\sqrt{l^2 + h^2}} - (-1) \right]$ |
| 8 | 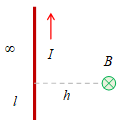 |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ 1 - \frac{(-l)}{\sqrt{l^2 + h^2}} \right]$ |
| 9 |  |
$\displaystyle\frac{\mu_0}{4\pi} \frac{I}{h} \left[ 1 - (-1) \right]$ |
Salah satu kasus yang amat dikenal adalah untuk kawat lurus panjang dengan medan magnetik diamati pada daerah di tengah-tengah kawat, yang pada Tabel 1 tercantum pada baris terakhir (kasus nomor 9) berupa
\begin{equation}\label{eqn:biot-savart-law-straight-wire-long-both-end} B = \frac{\mu_0 I}{2\pi h} \end{equation}
dan untuk kawat lurus panjang dengan medan magnetik diamati pada daerah di ujung kawat
\begin{equation}\label{eqn:biot-savart-law-straight-wire-long-one-end} B = \frac{\mu_0 I}{4\pi h} \end{equation}
yang tercantum pada Tabel 1 di dua baris terakhir (kasus bernomor 7 dan 8) dengan $l = 0$.

Gambar 3. Medan magnetik yang disebabkan oleh
kawat lurus panjang semi tak-hingga (kiri) dan kawat lurus panjang tak-hingga (kanan).
Dua buah kawat lurus panjang semi tak-hingga digabungkan, medan magnetik yang disebabkan keduanya akan menjadi seperti medan magnetik yang disebabkan oleh sebuah kawat lurus panjang tak-hingga. Ilustrasi mengenai kedua kasus ini diberikan pada Gambar 3.
— Sparisoma Viridi (@6unpnp) February 27, 2022