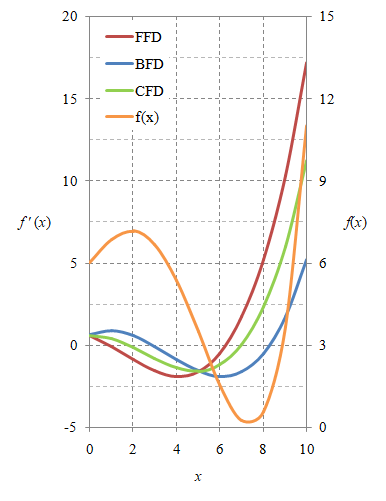
Gambar 1. Sebuah fungsi $f(x)$ dan turunan fungsi tersebut dengan pendekatan beda maju (FFD), beda mundur (BFD), dan beda tengah (CFD).
Diferensial dapat didekati secara numerik dengan beda hingga [1].
Suatu fungsi $f(x)$ dapat dituliskan dalam bentuk deret Taylor
\begin{equation}\label{eqn:taylor-series-of-a-function} f(x) = \sum_{n = 0}^N \left. \frac{d^n f(x)}{dx^n} \right|_{x = x_0} \frac{(x - x_0)^n}{n!}, \end{equation}
Deret Maclaurin, yang merupakan deret Taylor di sekitar nol atau $x_0 = 0$, memiliki bentuk
\begin{equation}\label{eqn:maclaurin-series-of-a-function} f(x) = \sum_{n = 0}^N \left. \frac{d^n f(x)}{dx^n} \right|_{x = 0} \frac{x^n}{n!}, \end{equation}
untuk sembarang fungsi $f(x)$ yang memiliki turunan ke-$N$.
Sebagai ilustrasi yang paling sederhana untuk Persamaan \eqref{eqn:maclaurin-series-of-a-function} dapat digunakan suatu fungsi polinomial, e.g $f(x) = c_0 + c_1 x + c_2 x^2$, yang akan memberikan
\[\frac{d^0 f(x)}{dx^0} = c_0 + c_1 x + c_2 x^2,\] \[\frac{d^1 f(x)}{dx^1} = c_1 + 2 c_2 x,\] \[\frac{d^2 f(x)}{dx^2} = 2 c_2.\]Ketiga persamaan terakhir untuk $x = 0$ akan menjadi
\[\left. \frac{d^0 f(x)}{dx^0} \right|_{x = 0} = \frac{d^0 f(0)}{dx^0} = c_0,\] \[\left. \frac{d^1 f(x)}{dx^1} \right|_{x = 0} = \frac{d^1 f(0)}{dx^1} = c_1,\] \[\left. \frac{d^2 f(x)}{dx^2} \right|_{x = 0} = \frac{d^2 f(0)}{dx^2} = 2 c_2.\]Substitusi ketiga persamaan terakhir ke Persamaan \eqref{eqn:maclaurin-series-of-a-function} akan menghasilkan
\[\begin{array}{rcl} f(x) & = & \displaystyle \sum_{n = 0}^N \left. \frac{d^n f(x)}{dx^n} \right|_{x = 0} \frac{x^n}{n!} \newline & = & \displaystyle c_0 \cdot \frac{x^0}{0!} + c_1 \cdot \frac{x^1}{1^2} + 2c_2 \cdot \frac{x^2}{2!} \newline & = & c_0 + c_1 x + c_2 x^2, \end{array}\]yang memberikan kembali $f(x)$. Suku-suku lebih tinggi tidak perlu dihitung karena turunan $f(x)$ bernilai nol untuk $n > 2$.
Bila hanya digunakan dua suku pertama pada ruas kanan Persamaan \eqref{eqn:taylor-series-of-a-function} maka
\begin{equation}\label{eqn:fuction-two-first-terms} f(x) \approx f(x_0) + f’(x_0) (x - x_0). \end{equation}
Dengan $\Delta x = x - x_0$ dan $x = x_0 + \Delta x$ Persamaan \eqref{eqn:fuction-two-first-terms} dapat dituliskan menjadi
\begin{equation}\label{eqn:fuction-two-first-terms-x0} f(x_0 + \Delta x) \approx f(x_0) + f’(x_0) \Delta x. \end{equation}
Perkenalkan simbol baru $x \equiv x_0$ sehingga Persamaan \eqref{eqn:fuction-two-first-terms-x0} menjadi
\begin{equation}\label{eqn:fuction-two-first-terms-x} f(x + \Delta x) \approx f(x) + f’(x) \Delta x \end{equation}
yang akan memberikan
\begin{equation}\label{eqn:finite-difference-1} f’(x) \approx \frac{f(x + \Delta x) - f(x)}{\Delta x}. \end{equation}
Bila didefinisikan $\Delta x = x_0 - x$ dan $x_0 = x + \Delta x$, maka dapat diperoleh bentuk yang mirip dengan Persamaan \eqref{eqn:finite-difference-1} dalam bentuk
\begin{equation}\label{eqn:finite-difference-2} f’(x) \approx \frac{f(x) - f(x - \Delta x)}{\Delta x}. \end{equation}
Pendekatan beda hingga meliputi beda hingga maju (FFD atau forward finite difference)
\begin{equation}\label{eqn:finite-difference-forward} f’(x) \approx \frac{f(x + \Delta x) - f(x)}{\Delta x}. \end{equation}
beda hingga mundur (BFD atau backward finite difference)
\begin{equation}\label{eqn:finite-difference-backward} f’(x) \approx \frac{f(x) - f(x - \Delta x)}{\Delta x}. \end{equation}
dan beda hingga tengah (CFD atau central finite difference)
\begin{equation}\label{eqn:finite-difference-central} f’(x) \approx \frac{f(x + \Delta x) - f(x - \Delta x)}{2\Delta x}. \end{equation}
Persamaan \eqref{eqn:finite-difference-central} dapat diperoleh dari Persamaan \eqref{eqn:finite-difference-forward} dan \eqref{eqn:finite-difference-backward}.

Gambar 1. Sebuah fungsi $f(x)$ dan turunan fungsi tersebut dengan pendekatan beda maju (FFD), beda mundur (BFD), dan beda tengah (CFD).
Pada Gambar 1 digunakan nilai $\Delta x = 1$, yang cukup besar, hanya agar terlihat perbedaan dari ketiga pendekatan beda hingga pada Persamaan \eqref{eqn:finite-difference-forward}, \eqref{eqn:finite-difference-backward}, dan \eqref{eqn:finite-difference-central}, untuk
\[f(x) = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 x^4\]sebagai fungsinya dengan $c_0 = 6$, $c_1 = 1$, $c_2 = -0.05$, $c_3 = -0.1$, dan $c_4 = 0.01$.
Turunan yang diperoleh secara numerik $f’_{\rm num}(x)$ dapat dibandingkan dengan turunan fungsinya secara langsung $f’(x)$ yang diperleh secara analitik
 |
 |
 |
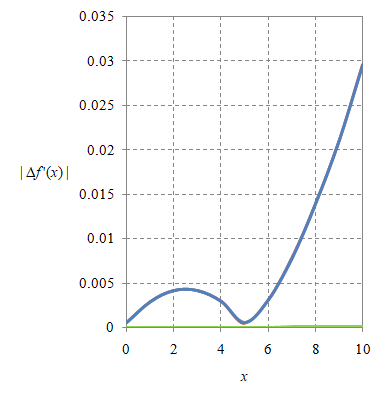 |
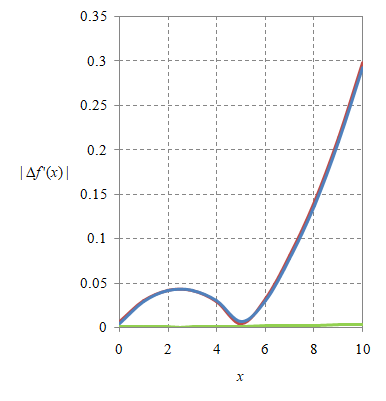
Gambar 2. Nilai absolut selisih turunan numerik dan turunan analitik untuk berbagai nilai $\Delta x$: (a) 10, (b) 1, (c) 0.1, dan (d) 0.01.
Arti warna garis yang digunakan pada Gambar 2 untuk pendekatan FFD, BFD, dan CFD sama dengan pada Gambar 1. Hanya pada gambar terakhir ini
\begin{equation}\label{eqn:dfx-num-the} |\Delta f’(x)| = |f’_{\rm num}(x) - f’(x)| \end{equation}
merupakan persamaan yang digunakan.
Dari Gambar 2 dapat diperoleh bahwa dengan semakin kecil nilai $\Delta x$ akan semakin kecil selisih $f’_{\rm num}(x)$ dengan f’(x) atau kesalahan yang dibuat oleh pendekatan numerik semakin kecil.