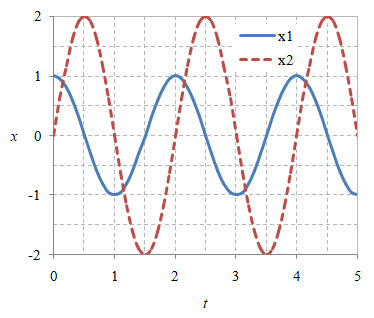
Gambar 1. Fungsi $c_1 x_1$ dan $c_2 x_2$, serta penjumlahannya yang tidak pernah bernilai nol untuk semua $x$ bila $c_1 = 1 \ne 0$ dan $c_2 = 2 \ne 0$.
Persamaan diferensial biasa (PDB) atau ordinary differential equation (ODE) adalah merupakan suatu kesamaan yang melibatkan suatu fungsi dan turunannya [1]. Dalam pengenalan PDB dapat diselesaikan beberapa persamaan diferensial tertentu seperti persamaan skalar order pertama, persamaan linier orde kedua, dan sistem persamaan linier [2]. Untuk persamaan diferensial dengan lebih dari satu variabel, misalnya persamaan panas, metode separasi variabel akan menghasilkan satu PDB untuk masing-masing variabel [3].
Terdapat pembagian PDB menjadi [4]
Di sini hanya akan dibahas jenis yang kedua, yaitu PDB linier.
Suatu PDB berorde $n$ dituliskan dalam bentuk
\begin{equation}\label{eqn:ode-nth-order} F\left(x, y, y’, \dots, y^{(n)}\right) = 0 \end{equation}
dengan
\begin{equation}\label{eqn:ode-y-x} y = y(x) \end{equation}
dan
\begin{equation}\label{eqn:ode-y-derivative} y^{(n)} = \frac{dy}{dx} \end{equation}
merupakan turunan ke $n$ dari $y$ terhadap $x$. Perhatikan bahwa notasi yang digunakan adalah pangkat $(n)$ dan bukan $n$, karena yang pertama berarti turunan ke $n$ sedangkan yang kedua berarti pangkat $n$.
Suatu PDB orde $n$ dikatakan linier bila berbentuk
\begin{equation}\label{eqn:ode-liniear} \sum_{j = 0}^n a_j(x) y^{(j)} = Q(x). \end{equation}
Perhatikan bahwa $a_j(x)$ dapat berbentuk apa saja asalkan bukan fungsi dari $y$ dan turunannya.
Bila $Q(x) = 0$ maka Persamaan \eqref{eqn:ode-liniear} akan menjadi
\begin{equation}\label{eqn:ode-liniear-homogeneous} \sum_{j = 0}^n a_j(x) y^{(j)} = 0 \end{equation}
sehingga memiliki sifat tambahan yang disebut sebagai homogen.
Secara umum suatu PDB berorde $n$ memiliki $n$ buah solusi yang saling bebas linier. Lebih jauh, semua kombinasi linier dari solusi fungsi-fungsi bebas linier yang diperoleh, juga merupakan solusi.
Suatu sistem pegas-benda yang berada pada lantai yang licin akan memberikan persamaan
\begin{equation}\label{eqn:spring-mass-system-newton-2-x-direction} ma = -kx \end{equation}
untuk arah $x$ yang diperoleh dari hukum II Newton. Terdapat hubungan
\begin{equation}\label{eqn:kinematics-a-v} a = \frac{dv}{dt} \end{equation}
dan
\begin{equation}\label{eqn:kinematics-v-x} v = \frac{dx}{dt} \end{equation}
yang akan membuat Persamaan \eqref{eqn:spring-mass-system-newton-2-x-direction} menjadi
\begin{equation}\label{eqn:ode-spring-mass-system-1} m \frac{d^2x}{dt^2} = -kx \end{equation}
yang dapat dituliskan lebih lanjut menjadi
\begin{equation}\label{eqn:ode-spring-mass-system-2} m \frac{d^2x}{dt^2} + kx = 0 \end{equation}
sehingga sesuai dengan Persamaan \eqref{eqn:ode-liniear-homogeneous}, yang menyatakan bahwa PDB dari sistem pegas-massa merupakan suatu PDB linier dan homogen. Persamaan \eqref{eqn:ode-spring-mass-system-2} dapat dituliskan menjadi
\begin{equation}\label{eqn:ode-spring-mass-system-y(x)} m y’’ + ky = 0, \end{equation}
bila menggunakan simbol-simbol pada Persamaan \eqref{eqn:ode-liniear-homogeneous}. Perhatikan bahwa notasi pada Persamaan \eqref{eqn:ode-spring-mass-system-2} adalah $x$ dan $t$ sedangkan pada Persamaan \eqref{eqn:ode-liniear-homogeneous} adalah $y$ dan $x$.
Selanjutnya agar tidak mengaburkan sistem fisis yang direpresentasikan, digunakan simbol $x$ dan $t$, yang akan menghasilkan solusi dari Persamaan \eqref{eqn:ode-spring-mass-system-2} berupa
\begin{equation}\label{eqn:ode-spring-mass-system-solution-1} x_1 = A \cos \omega t \end{equation}
dan
\begin{equation}\label{eqn:ode-spring-mass-system-solution-2} x_2 = B \sin \omega t \end{equation}
dengan
\begin{equation}\label{eqn:ode-spring-mass-system-solution-omega} \omega = \sqrt{\frac{k}{m}}. \end{equation}
Persamaan \eqref{eqn:ode-spring-mass-system-solution-1} dan \eqref{eqn:ode-spring-mass-system-solution-2} saling bebas linier, di mana, dengan $c$ suatu konstanta, tidak dapat diperoleh bahwa
\[x_2 = c x_1,\]atau sebaliknya $x_1$ tidak dapat dinyatakan dalam $x_2$ [5]. Selain dengan cara tersebut, dapat pula saling bebas linier antara $x_1$ dan $x_2$ diperoleh dari
\[c_1 x_1 + c_2 x_2 = 0\]untuk semua $x$ hanya dapat dipenuhi bila $c_1 = 0$ dan $c_2 = 0$. Selanjutnya, kedua solusi tersebut dapat digambarkan berikut ini.

Gambar 1. Fungsi $c_1 x_1$ dan $c_2 x_2$, serta penjumlahannya yang tidak pernah bernilai nol untuk semua $x$ bila $c_1 = 1 \ne 0$ dan $c_2 = 2 \ne 0$.
Dikarenakan $x_1$ dan $x_2$ merupakan solusi maka kombinasi linier dari keduanya
\begin{equation}\label{eqn:linear-combination} x_3 = c_1 x_1 + c_2 x_2 \end{equation}
juga merupakan solusi. Selanjutnya Persamaan \eqref{eqn:ode-spring-mass-system-2} yang merupakan PDB linier homogen orde kedua memiliki dua solusi yang saling bebas linier, seperti telah diberikan pada Persamaan \eqref{eqn:ode-spring-mass-system-solution-1} dan \eqref{eqn:ode-spring-mass-system-solution-2}.
Tentukan dari persamaan-persamaan berikut yang merupakan persamaan diferensial biasa linier.
a. $y’’’ \tan x = \ln y$.
b. $10x^2 - \cos y = y’’$.
c. $y’’ + 2xy’ + \sin x = 0$.
d. $(y’)^2 + y’’ = 2x$.
e. $\sqrt{y’’} - x + 2y + 10y’’ = 0$.
Tentukan dari persamaan-persamaan berikut yang persamaan diferensial biasa linier yang homogen.
a. $y + x^2 y’’ + \tan x = 0$.
b. $7x y’’’ - 2\sqrt{x} y’’ = y$.
c. $y’’’ = y’ \exp(x^2)$.
d. $y’ + y = 2x$.
e. $y’’’ + y’’ + y + x = 0$.
Pada benda jatuh bebas dengan memperhitungkan gesekan udara, akan diperoleh persamaan $ma = -bv$. Tentukan sifat yang paling tepat persamaan diferensial ini dari sifat-sifat berikut.
a. Bukan persamaan diferensial.
b. Bukan persamaan diferensial biasa.
c. Persamaan diferensial biasa.
d. Persamaan diferensial biasa linier.
e. Persamaan diferensial biasa linier dan homogen.
Tentukan sistem fisis mana yang termasuk akan menghasilkan persamaan diferensial biasa linier dan tak-homogen.
a. Sistem pegas benda di atas lantai mendatar kasar.
b. Sistem pegas benda di atas lantai mendatar licin.
c. Sistem pegas vertikal tanpa gesekan udara.
d. Sistem pegas vertikal dengan gesekan udara.
e. Sistem pegas vertikal tanpa gesekan udara dengan gaya luar fungsi waktu.
Tunjukkan bagaimana kombinasi linier dari solusi, seperti pada Persamaan \eqref{eqn:linear-combination}, juga merupakan solusi suatu persamaan diferensial.
— Sparisoma Viridi (@6unpnp) March 15, 2022