
Kapasitor merupakan devais untuk menyimpan energi listrik, yang tersusun atas dua konduktor dalam jarak dekat dan terisolasi secara listrik satu dengan lainnya [1]. Terdapat setidaknya tiga geometri kapasitor yang umum [2], yang memiliki karakter yang mirip saat jarak antar pelat diubah [3].
Untuk menyatakan sebuah kapasitor umumnya digunakan variabel $C$, yang disimbolkan dengan —| |—, di mana garis horisontal menggambarkan kawat konektor dan dua garis tegak menggambarkan kapasitor pelat sejajar. Satuan kapasitansi, kemampuan kapasitor untuk menyimpan energi berbentuk muatan listrik, adalah farad atau F.
Kapasitansi adalah sifat listrik konduktor atau rangkaian konduktor yang mengukur jumlah muatan listrik yang terpisahkan (positif saja atau negatif saja) yang dapat tersimpan pada konduktor untuk setiap satuan perubahan beda potensial [4], di mana untuk kapasitor menjadi
\begin{equation}\label{eqn:capacitance} C = \frac{Q}{V} \end{equation}
di mana $C$ adalah kapasitansi, $Q$ muatan yang tersimpan dalam kapasitor, dan $V$ adalah beda potensial antara kedua pelat kapasitor.
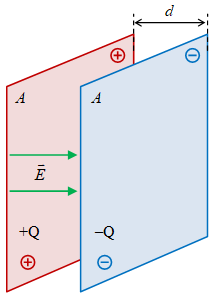
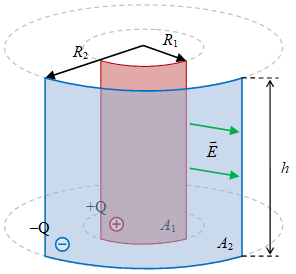
Terdapat tiga geometri kapasitor yang umum dibahas yaitu pelat sejajar, pasangan kulit bola, dan pasangan kulit silinder [2].
Tabel 1. Berbagai jenis geometri kapasitor dan kapasitansinya.
Untuk kapasitor pasangan kulit bola pada Tabel 1 pelat meliputi kulit bola utuh. Digambarkan hanya sebagian agar terlihat parameter masing-masing pelat yang meliputi radius, luas, muatan, serta arah medan listriknya.
Untuk jari-jari yang luas $R_1 > > \Delta R$ dan $R_2 > > \Delta R$ dengan $R_2 = R_1 + \Delta R$ akan membuat Persamaan $\rm(1b)$ dapat dituliskan menjadi
\[\begin{array}{rcl} C & = & \displaystyle \epsilon_0 \frac{4 \pi R_1 R_2}{R_2 - R_1} \newline & = & \displaystyle \epsilon_0 \frac{4 \pi R_1 (R_1 + \Delta R)}{\Delta R} \newline & \approx & \displaystyle \epsilon_0 \frac{4 \pi R_1^2}{\Delta R} \newline \end{array}\]dengan jarak antar pelat $d = \Delta R$ dan luas pelat $A = 4\pi R_1^2$ akan menghasilkan
\[\epsilon_0 \frac{4 \pi R_1^2}{\Delta R} = \epsilon_0 \frac{A}{d},\]yang tak lain adalah Persamaan $\rm(1a)$.
Dengan menggunakan deret Taylor dapat diperoleh bahwa
\begin{equation}\label{eqn:taylor-series-r1-r2} \ln (R_1 + \Delta R) \approx \ln R_1 + \frac{\Delta R}{R_1} \end{equation}
yang dapat digunakan pada Persamaan $\rm(1c)$.
Kapasitor dapat disusun seri dan paralel, dengan kapasitor ekivalen untuk susunan seri adalah
\begin{equation}\label{eqn:series-arrangement} C_{\rm ser} = \sum_{i = 1}^{N} C_i \end{equation}
dan untuk susunan paralel adalah
\begin{equation}\label{eqn:parallel-arrangement} \frac{1}{C_{\rm par}} = \sum_{i = 1}^{N} \frac{1}{C_i} \end{equation}
yang dapat digunakan untuk menyederhanakan susunan kapasitor yang lebih kompleks.
— Sparisoma Viridi (@6unpnp) March 7, 2022