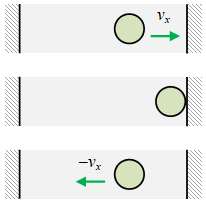
Gambar 1. Kecepatan partikel sebelum dan sesudah tumbukan elastik adalah $v_x$ dan $-v_x$.
Gas dapat dipelajari melalui aksi skala kecil dari setiap individu molekul atau melalui aksi skala besar gas secara keseluruhan, di mana untuk aksi skala besar pengukuran dapat dilakukan, akan tetapi untuk aksi skala kecil perlu menggunakan model teoretis, yang disebut TKG atau teori kinetik gas [1]. TKG ini didasarkan pada gambaran mengenai bahan secara molekuler [2]. Terdapat tiga [3], empat [4], atau lima [5] asumi yang digunakan dalam merumuskan teori ini.
Terdapat beberapa asumsi dalam membangung TKG.
Kelima asumsi di atas merupakan penyatuan dari asumsi-asumsi yang umum dinyatakan dalam TKG [3, 4, 5].
Setiap individu molekul memiliki sifat-sifat fisis standar seperti massa, momentum, dan energi.
Tabel 1. Besaran fisis untuk gas secara keseluruhan dan bagi molekul-molekulnya.
| Besaran | Gas | Molekul gas |
|---|---|---|
| densitas | $\rho$ | $\displaystyle \approx \frac{1}{V} \sum_i m_i$ |
| tekanan | $p$ | $\displaystyle \approx \frac{1}{A \Delta t} \sum_i I_i$ |
| temperatur | $T$ | $\displaystyle \approx \frac{1}{N}\sum_i \tfrac12 m_i v_i^2$ |
Penulisan formula pada kolom ketiga Tabel 1 belum atau bukan merupakan persamaan yang terkait langsung dengan besaran-besaran gas pada kolom keduanya. Mungkin terdapat konstanta lain atau proses pengolahan lain. Formula pada tabel di atas diberikan sebagai ilustrasi dulu.
Bila terdapat suatu besaran bagi sebuah partikel, misalnya massa $m_i$, maka rata-rata aritmatika untuk massa adalah
\begin{equation}\label{eqn-average-mass} \overline{m} = \frac{1}{N} \sum_{i = 1}^N m_i, \end{equation}
dengan $N$ adalah jumlah seluruh partikel yang dilibatkan dalam perhitungan. Rata-rata dapat pula untuk besaran yang dikuadratkan seperti kecepatan, misalnya dalam energi kinetik rata-rata
\begin{equation}\label{eqn-average-kinetic-energy} \begin{array}{rcl} \overline{K} & = & \displaystyle \frac{1}{N} \sum_{i = 1}^N \tfrac12 m_i v_i^2 \newline & = & \displaystyle \tfrac12 m \frac{1}{N} \sum_{i = 1}^N v_i^2 \newline & = & \displaystyle \tfrac12 m \overline{v^2}, \end{array} \end{equation}
dengan $m$ adalah massa setiap partikel yang sama nilainya. Kemudian, dikarenakan $\vec{v}$ adalah besaran vektor maka
\begin{equation}\label{eqn-v2} \begin{array}{rcl} v^2 & = & \vec{v} \cdot \vec{v} \newline & = & (v_x \hat{x} + v_y \hat{y} + v_z \hat{x}) \cdot (v_x \hat{x} + v_y \hat{y} + v_z \hat{x}) \newline & = & v_x^2 + v_y^2 + v_z^2 \end{array} \end{equation}
sehingga
\begin{equation}\label{eqn-v2-average} \begin{array}{rcl} \overline{v^2} & = & \overline{v_x^2 + v_y^2 + v_z^2} \newline & = & \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2}. \end{array} \end{equation}
Sebagai contoh bila terdapat $\vec{v}_1 = 2 \hat{x} + \hat{y} - 3 \hat{z}$, $\vec{v}_2 = 2 \hat{x} + 5 \hat{y} + 4 \hat{z}$, dan $\vec{v}_1 = 2 \hat{x} - 4 \hat{y} + 3 \hat{z}$, maka
\begin{equation}\label{eqn-v2-average-vxyz} \begin{array}{rcl} v_1^2 & = & 14, \newline v_2^2 & = & 45, \newline v_3^2 & = & 29, \newline \sum v_x^2 & = & 12, \newline \sum v_y^2 & = & 42, \newline \sum v_y^2 & = & 34, \newline \overline{v^2} & = & \overline{v_x^2} + \overline{v_y^2} + \overline{v_z^2} \newline \tfrac13 (14 + 45 + 29) & = & \tfrac13 \cdot 12 + \tfrac13 \cdot 42 + \tfrac13 \cdot 34 \newline \frac{88}{3} & = & \frac{88}{3}, \end{array} \end{equation}
yang menunjukkan berlakunya Persamaan \eqref{eqn-v2-average} melalui suatu contoh.
Sebuah partikel yang sedang bergerak pada arah $x$ memiliki kecepatan $v_x$ dan menumbuk dinding di depannya dengan tumbukan elastik dan berbalik arah dengan kecepatan $-v_x$.

Gambar 1. Kecepatan partikel sebelum dan sesudah tumbukan elastik adalah $v_x$ dan $-v_x$.
Perubahan momentumnya adalah
\begin{equation}\label{eqn-dpx} \Delta p_x = v_{x,f} - v_{x,i} = -2v_x, \end{equation}
dengan indeks $f$ dan $i$ berarti akhir (final) dan awal (inisial).
Lebar wadah pada arah $x$ adalah $L_x$, bila partikel bergerak dengan laju $v_x$, maka
\begin{equation}\label{eqn-dtx} \Delta t_x = \frac{2L_x}{v_x} \end{equation}
adalah selang waktu antar dua tumbukan berurutan.
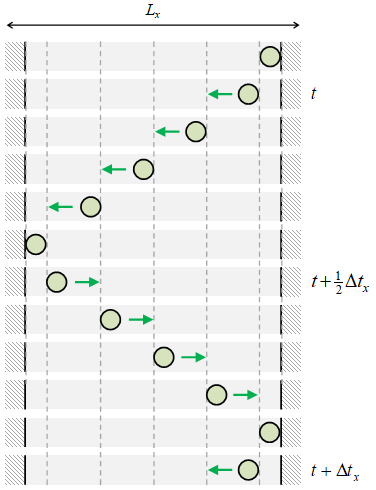
Gambar 2. Posisi partikel selama satu perjalanan bolak-balik $\Delta t_x$ pada arah lebar wadah $L_x$.
Saat partikel bergerak dari ujung kanan ke ujung kiri jarak yang ditempuhnya adalah $L_x$ dan saat kembali ke ujung kanan kembali jarak $L_x$ ditempuhnya, sehingga total jaraknya adalah $2L_x$. Dengan laju gerak partikel selalu sama $v_x$ maka selang waktu satu perjalanan bolak-balik adalah seperti diberikan oleh Persaamaan \eqref{eqn-dtx}. Di sini telah digunakan asumsi bahwa tumbukan bersifat elastik dan seketika.
Dari Persamaan \eqref{eqn-dpx} dapat diperoleh impuls pada dinding wadah
\begin{equation}\label{eqn-wall-impulse} I_{ \rm wall} = -I = -\Delta p_x = 2mv_x, \end{equation}
dengan tanda negatif impuls pada partikel berlawanan arah dengan impuls pada dinding. Selanjutnya, dengan beruntunnya tumbukan partikel pada dinding wadah dapat diperoleh
\begin{equation}\label{eqn-wall-average-force-x-1} \overline{F} _{x,1} = \frac{I _{\rm wall}}{\Delta t_x} = \frac{2 mv_x}{2 L_x / v_x} = \frac{mv_x^2}{L_x}, \end{equation}
yang merupakan gaya rata-rata yang dialami dinding akibat gerak partikel pada arah $x$ akibat satu partikel dan
\begin{equation}\label{eqn-wall-average-force-x-n} \overline{F} _{x,N} = N \frac{m \overline{v_x^2}}{L_x}, \end{equation}
adalah untuk $N$ partikel. Dengan asumsi
\begin{equation}\label{eqn-wall-average-vx2=vy2=vz2} \overline{v_x^2} = \overline{v_y^2} = \overline{v_z^2} \end{equation}
dan menggunakan Persamaan \eqref{eqn-v2-average} dapat diperoleh
\begin{equation}\label{eqn-wall-average-vx2-v2} \overline{v_x^2} = \tfrac13 \overline{v^2}, \end{equation}
sehingga Persamaan \eqref{eqn-wall-average-force-x-n} dapat dituliskan menjadi
\begin{equation}\label{eqn-wall-average-force-n} \overline{F} _{x,N} = \frac{N m \overline{v^2}}{3L_x}, \end{equation}
yang merupakan gaya rata-rata pada arah $x$ oleh $N$ buah partikel gas.
Wadah gas dapat disederhanakan menjadi wadah dengan ukuran $L_x \times L_y \times L_z$. Dan pada setiap sisi wadah yang diasumsikan berbentuk balok tersebut, terdapat gaya rata-rata seperti yang telah diberikan pada Persamaan \eqref{eqn-wall-average-force-n}.
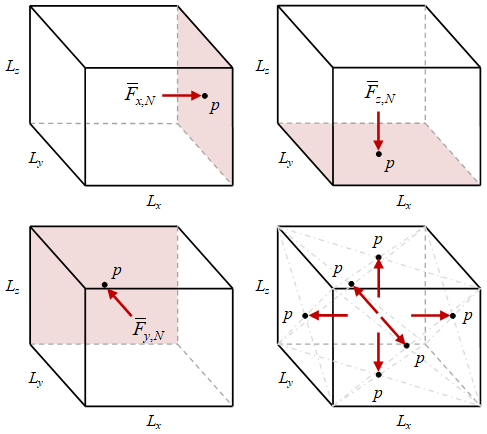
Gambar 3. Gaya pada rata-rata setiap arah $x$, $y$, dan $z$ oleh $N$ partikel gas.
Agar dapat diperoleh tekanan pada dinding sebelah kanan Persamaan \eqref{eqn-wall-average-force-n} perlu dibagi luas dinding tersebut
\begin{equation}\label{eqn-wall-x-pressure} p = \frac{\overline{F} _{x,N}}{A} = \frac{N m \overline{v^2}}{3L_x (L_y L_z)} = \frac{N m \overline{v^2}}{3V}, \end{equation}
dengan $V = L_x \times L_y \times L_z$ adalah volume wadah gas. Dengan cara yang sama akan diperoleh ungkapan tekanan yang sama untuk semua sisi wadah gas seperti pada Persamaan \eqref{eqn-wall-x-pressure}.
Dengan memanfaatkan Persamaan \eqref{eqn-average-kinetic-energy} dapat dituliskan bahwa
\begin{equation}\label{eqn-average-kinetic-energy-2} m \overline{v^2} = 2 \overline{K}, \end{equation}
yang akan membuat Persamaan \eqref{eqn-wall-x-pressure} menjadi
\begin{equation}\label{eqn-wall-pressure} p = \frac23 \frac{N}{V} \overline{K}. \end{equation}
Energi kinetik rata-rata semua partikel gas perlu diungkapkan dalam besaran yang lain.
Prinsip ekipartisi energi menyatakan bahwa total energi kinetik suatu sistem dibagi merata pada semua bagian yang saling tidak bergantung saat sistem mencapai kesetimbangan termal [6]. Untuk gas hanya dengan gerak translasi, terdapat gerak pada arah $x$, $y$, dan $z$, maka masing-masing arah berkontribusi sebesar $\frac12 kT$ untuk tiap molekulnya
\begin{equation}\label{eqn-average-energy-kinetic-x} \overline{K_x} = \tfrac12 m \overline{v_x^2} = \tfrac12 kT, \end{equation}
\begin{equation}\label{eqn-average-energy-kinetic-y} \overline{K_y} = \tfrac12 m \overline{v_y^2} = \tfrac12 kT, \end{equation}
\begin{equation}\label{eqn-average-energy-kinetic-z} \overline{K_z} = \tfrac12 m \overline{v_z^2} = \tfrac12 kT, \end{equation}
dengan $k = 1.38066 \times 10^{-23} \ \rm J/K$ adalah konstanta Boltzmann. Selanjutnya, secara keseluruhannya
\begin{equation}\label{eqn-average-energy-kinetic-kt} \begin{array}{rcl} \overline{K} & = & \overline{K_x} + \overline{K_y} + \overline{K_z} \newline & = & \tfrac12 kT + \tfrac12 kT + \tfrac12 kT \newline & = & \tfrac32 kT \end{array} \end{equation}
adalah rata-rata energi kinetik total per molekul [7].
Substitusi Persamaan \eqref{eqn-average-energy-kinetic-kt} ke Persamaan \eqref{eqn-wall-pressure} akan mendapatkan
\begin{equation}\label{eqn-ideal-gas-law} \begin{array}{rcl} p & = & \displaystyle \frac23 \frac{N}{V} \overline{K} \newline & = & \displaystyle \frac23 \frac{N}{V} \ \left( \tfrac32 kT \right) \newline & = & \displaystyle \frac{NkT}{V}, \newline pV & = & NkT \end{array} \end{equation}
hukum gas ideal, yang lebih dikenal dengan bentuk [8]
\begin{equation}\label{eqn-ideal-gas-law-2} pV = nRT, \end{equation}
dengan $n$ jumlah mol gas, $R$ konstanta gas, dan $T$ temperatur. Terdapat persamaan [9]
\begin{equation}\label{eqn-ideal-gas-law-k-r-na} R = k N_{\rm A}, \end{equation}
yang menghubungkan antara konstanta gas $R = 8.32441 \ \rm J \cdot K^{-1} \cdot mol^{-1}$, konstanta Boltzmann $k$, dan bilangan Avogadro $N_{\rm A} = 6.022 \times 10^{23} \ \rm mol^{-1}$.
newton’s laws of motion • momentum • kinetic energy • impulse