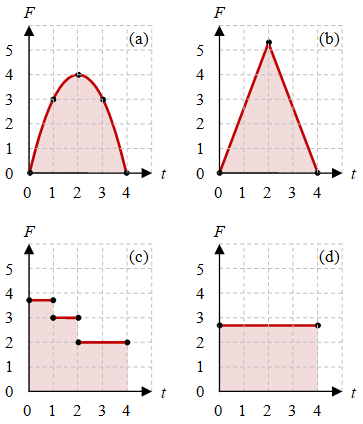
Gambar 1. Beberapa bentuk gaya sebagai fungsi waktu $F(t)$ yang bekerja selama $\Delta t = 4$ dan menghasilkan impuls yang sama.
Impuls merupakan perkalian dari nilai rata-rata gaya dan rentang waktu selama gaya tersebut bekerja atau perubahan momentum yang dihasilkan gaya tersebut [1], atau lebih umum merupakan integral dari gaya selama selang waktu bekerjanya gaya tersebut [2]. Penggunaan utama dari konsep ini adalah untuk mempelajari gaya impak rata-rata selama tumbukan, dikarenakan massa dan perubahan kecepatan umumnya diukur akan tetapi kecepatan selama tumbukan tidak [3].
Bila diketahui fungsi waktu dari gaya $\vec{F}(t)$, impuls dapat diperoleh melalui
\begin{equation}\label{eqn-impulse-force-integral} \vec{I} = \int \vec{F} dt \end{equation}
atau bila menggunakan gaya rata-rata $\vec{F}_{\rm avg}$
\begin{equation}\label{eqn-impulse-force-average} \vec{I} = \vec{F}_{\rm avg} \Delta t, \end{equation}
dan
\begin{equation}\label{eqn-impulse-momentum-change} \vec{I} = \Delta \vec{p}, \end{equation}
bila terkait dengan perubahan momentum $\Delta \vec{p}$, di mana
\begin{equation}\label{eqn-momentum-change-constant-mass} \Delta \vec{p} = m \Delta \vec{v}, \end{equation}
bila selama tumbukan massa benda tidak berubah.
Idealnya gaya yang menyebabkan impuls dapat diketahui bentuk fungsinya sehingga Persamaan \eqref{eqn-impulse-force-integral} dapat digunakan. Akan tetapi bila tidak diketahui bentuk $\vec{F}(t)$, yang umumnya terjadi di dalam pengamatan atau eksperimen, digunakan gaya rata-rata $\vec{F}_{\rm avg}$ sebagai pendekatannya seperti diberikan oleh Persamaan \eqref{eqn-impulse-force-average}.

Gambar 1. Beberapa bentuk gaya sebagai fungsi waktu $F(t)$ yang bekerja selama $\Delta t = 4$ dan menghasilkan impuls yang sama.
Bentuk gaya rata-rata $F_{\rm avg}$ diberikan pada Gambar 1(d) yang dapat dianggap mewakili kurva-kurva $F(t)$ yang lain, (a), (b), (c), bila bentuk sebenarnya tidak diketahui. Keempat kurva $F(t)$ pada gambar di atas memberikan nilai impuls yang sama $10 \frac23$, yang merupakan luas daerah di bawah kurva. Daerah yang dimaksud telah ditandai dengan warna merah. Gaya sebagai fungsi waktu $F(t)$ untuk Gambar 1 (a)-(d) adalah
\begin{equation}\label{eqn-impulse-force-func-a} F(t) = 4t - t^2, \end{equation}
\begin{equation}\label{eqn-impulse-force-func-b} F(t) = \left\{ \begin{array}{rcl} \frac83 t, & 0 \le t \le 2, \newline -\frac83 t(x-2) + \frac{16}3, & 2 \le t \le 4, \newline \end{array} \right. \end{equation}
\begin{equation}\label{eqn-impulse-force-func-c} F(t) = \left\{ \begin{array}{rcl} \frac83, & 0 \le t \le 1, \newline 3, & 1 \le t \le 2, \newline 2, & 2 \le t \le 4, \end{array} \right. \end{equation}
\begin{equation}\label{eqn-impulse-force-func-d} F(t) = \tfrac83. \end{equation}
Fungsi pada Persamaan \eqref{eqn-impulse-force-func-a} dan \eqref{eqn-impulse-force-func-d} tidak perlu diberi rentang karena kebetulan merupakan fungsi malar atau kontinu dalam selang waktu gaya tersebut bekerja, yaitu $0 \le t \le 4$.
Sebelum berinteraksi dengan gaya $\vec{F}$ momentum suatu benda adalah $\vec{p}(t_1)$ dan setelah berinteraksi menjadi $\vec{p}(t_1 + \Delta t)$ dengan $\Delta t$ adalah durasi gaya bekerja atau $\vec{F}(t)$ hanya berlaku saat $t_1 \le t \le t_1 + \Delta t$, yang dapat dituliskan dalam bentuk
\begin{equation}\label{eqn-impulse-force-func-e} F(t) = \left\{ \begin{array}{rcl} 0, & t \le t_1, \newline f(t), & t_1 \le t \le t_1 + \Delta t, \newline 0, & t_1 + \Delta t \le t, \end{array} \right. \end{equation}
dengan $f(t)$ suatu fungsi kontinu.
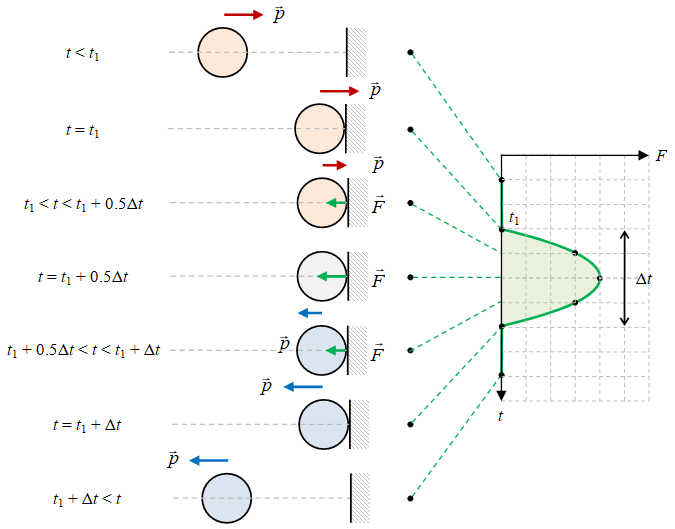
Gambar 2. Ilustrasi sebuah bola menumbuk dinding dengan keadaan awal ($\color{#fcc}{\blacksquare}$) sebelum peristiwa tumbukan, saat impuls bekerja ($\color{#ccc}{\blacksquare}$) selama peristiwa tumbukan, dan keadaan akhirnya ($\color{#ccf}{\blacksquare}$) setelah peristiwa tumbukan.
Dengan menggunakan fungsi gaya berbentuk kuadratik seperti pada Gambar 1(a) dapat digambarkan ilustrasi perubahan momentum benda sebelum, saat, dan setelah peristiwa tumbukan seperti diberikan pada Gambar 2. Telah jelas terlihat bagaimana momentum benda, setelah mulai menyentuh dinding, perlahan-lahan mengecil, menjadi nol, lalu mulai berbalik arah.
velocity • newton’s 2nd law • momentum