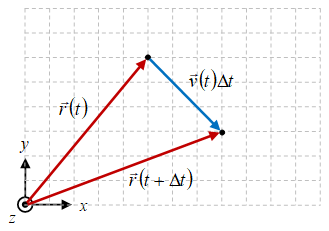
Gambar 1. Penjumlahan vektor dari $\vec{r}(t)$ dan $\vec{v}(t) \Delta t$ yang menghasilkan $\vec{r}(t + \Delta t)$.
Velocity adalah turunan dari posisi terhadap waktu [1], yang merupakan besaran vektor [2], dan memiliki satuan panjang dibagi dengan waktu [3], yang dapat pula dirujuk sebagai kecepatan sesaat [4].
Dalam satuan SI (Système International) kecepatan dinyatakan dengan satuan panjang dibagi satu waktu, yaitu $\rm m/s$ atau meter per detik [5]. Sebaiknya suatu vektor kecepatan dituliskan dalam bentuk
\[\vec{v} = 1.25 \times 10^{-1} \cdot \left( \frac23 \hat{x} + \frac13 \hat{y} - \frac23 \hat{z} \right) \cdot {\rm m \ s^{-1}},\]dengan bagian pertama menunjukkan besar dalam notasi ilmiah, bagian kedua merupakan vektor satuan, dan bagian terakhir merupakan satuan dalam SI.
Kecepatan merupakan laju perubahan posisi pada selang waktu tertentu
\begin{equation}\label{eqn-1a} \vec{v} = \lim_{\Delta t \to 0} \frac{\vec{r}(t + \Delta t) - \vec{r}(t)}{\Delta t} = \frac{d\vec{r}}{dt}, \end{equation}
dengan ilustrasinya diberikan pada Gambar 1 berikut.

Gambar 1. Penjumlahan vektor dari $\vec{r}(t)$ dan $\vec{v}(t) \Delta t$ yang menghasilkan $\vec{r}(t + \Delta t)$.
Dengan menggunakan penjumlahan vektor dapat diperoleh dari Gambar 1 bahwa
\begin{equation}\label{eqn-1b} \vec{r}(t + \Delta t) = \vec{r}(t) + \vec{v}(t) \Delta t, \end{equation}
yang akan dapat dituliskan menjadi
\begin{equation}\label{eqn-1c} \vec{v}(t) \Delta t = \vec{r}(t + \Delta t) - \vec{r}(t) \end{equation}
dan
\begin{equation}\label{eqn-1d} \vec{v}(t) = \frac{\vec{r}(t + \Delta t) - \vec{r}(t)}{\Delta t}, \end{equation}
dengan $\vec{v}(t)$ belum merupakan kecepatan melainkan kecepatan rata-rata. Untuk menjadi kecepatan atau kecepatan sesaat Persamaan \eqref{eqn-1d} perlu dicari limitnya untuk $\Delta t \to 0$ seperti pada Persamaan \eqref{eqn-1a}.
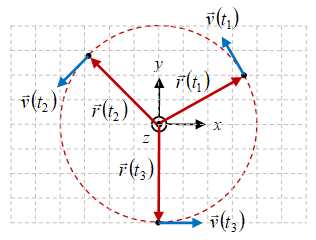
Gambar 1. Arah vektor kecepatan $\vec{v}$ yang selalu tegak lurus dengan vektor posisinya $\vec{r}$ pada gerak melingkar beraturan.
Arah vektor kecepatan $\vec{v}$ terhadap vektor posisi $\vec{r}$ tidak keterkaitan yang pasti kecuali untuk beberapa kasus, yang salah satunya adalah gerak melingkar beraturan (GMB), di mana arah vektor kecepatannya $\vec{v}$ selalu tegak lurus dengan vektor posisinya $\vec{r}$ pada setiap saat $t$. Ilustasi mengenai hal ini diberikan dalam Gambar Gambar 2 sebelumnya, dengan pusat koordinat diambil pada pusat lintasan. Simulasi mengenai sistem ini dapat dilihat menggunakan simulasi PhET [6].
Fungsi kecepatan $v$ dapat diperoleh dari fungsi percepatan $a$ melalui
\begin{equation}\label{eqn-2} v = \int a \ dt \end{equation}
dengan menggunakan integral. Persamaan \eqref{eqn-2} menggambarkan hubungan untuk kasus 1-d, sedangkan untuk 2-d dan 3-d dapat dituliskan
\begin{equation}\label{eqn-3} \vec{v} = \int \vec{a} \ dt \end{equation}
dengan menggunakan notasi vektor, yang akan menjadi
\begin{equation}\label{eqn-4} \vec{v} - \vec{v}_0 = \int _{t_0}^t \vec{a} \ dt \end{equation}
bila terdapat syarat awal $\vec{v}_0 = \vec{v}(t_0)$. Perhatikan bahwa $\vec{v} = \vec{v}(t)$ adalah fungsi kecepatan.
position • position velocity • velocity acceleration • kinematics graphs • vector 2d add