Kurang baiknya pemahaman mengenai grafik kinematika, e.g. $x-t$, $v-t$, $a-t$, merupakan studi yang menarik karena terdapat berbagai kebingungan [1], yang masih teramati sampai beberapa saat yang lalu [2]. Salah satu pendekatan untuk membantu pemahaman dilakukan dengan memanfaatkan alat bantu microcomputer based laborator atau MBL [3]. Dan untuk menyelamai lebih dalam, pengamatan pergerakan mata saat peserta mengerjakan tes terkait materi ini pun dilakukan [4]. Hal ini menunjukkan pentingnya peran grafik kinematika dalam fisika. Gerak lurus dengan percepatan yang merupakan fungsi waktu dapat pula dianalisis menggunakan grafik selain dengan kalkulus [5]. Kemudahan menggambarkan grafik pun telah banyak tersedia secara daring, walau masih dengan variabel dummy $y - x$ [6].
Hubungan antara fungsi posisi $x$, kecepatan $v$, dan percepatan $a$ dapat digambarkan dalam Tabel 1 berikut.
Tabel 1. Relasi antar fungsi-fungsi posisi $x$, kecepatan $v$, dan percepatan $a$.
| $x-v$ | $v-a$ | |
|---|---|---|
| $ \displaystyle \frac{d}{dt}$ | $ \displaystyle v = \frac{dx}{dt} $ | $ \displaystyle a = \frac{dv}{dt} $ |
| $\displaystyle \int dt$ | $ \displaystyle x = \int v \ dt $ | $ \displaystyle v = \int a \ dt $ |
Perhatikan bahwa perlu digunakan diferensial $(d/dt)$ dan integral $(\int dt)$ untuk memperoleh $v$ dari $x$ dan sebaliknya, serta $a$ dari $v$ dan sebaliknya.
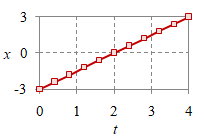
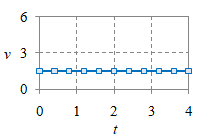
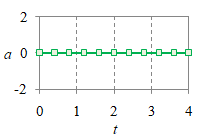
Gerak lurus dengan kecepatan tetap disebut sebagai GLB (gerak lurus beraturan). Hubungan antara fungsi posisi $x$, kecepatan $v$, dan percepatannya $a$ diberikan oleh Gambar 1 berikut.
 |
$x = \frac32t - 3$ |
 |
$v = \frac32$ |
 |
$a = 0$ |
Gambar 1. Grafik posisi $x$ (atas), kecepatan $v$ (tengah), dan percepatan $a$ (bawah) suatu GLB.
Dengan menggunakan relasi dalam Tabel 1 dapat diperiksa persamaan-persamaan dalam Gambar 1.
Gerak lurus dengan kecepatan berubah bersifat umum, yang termasuk di dalamnya adalah gerak lurus dengan percepatan tetap ($a \ne 0$) yang dikenal sebagai GLBB (gerak lurus berubah beraturan). Gambar 2 memberikan ilustrasi hubungan antara fungsi posisi $x$, kecepatan $v$, dan percepatannya $a$.
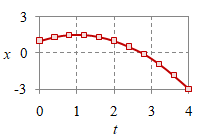 |
$x = -\frac12t^2 + t + 1$ |
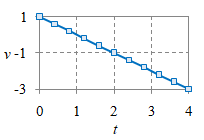 |
$v = -t + 1$ |
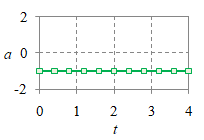 |
$a = -1$ |
Gambar 2. Suatu GLBB dan grafik posisi $x$ (atas), kecepatan $v$ (tengah), dan percepatannya $a$ (bawah).
Perhatikan bahwa dengan menggunakan hubungan dalam Tabel 1 dapat diperoleh $v$ dari $x$ dan kemudian $a$ dari $v$ pada Gambar 2.
Gerak lurus dengan percepatan berubah [5], selain GLBB, meliputi pula gerak konsekutif dengan percepatan bernilai tetap tertentu untuk suatu selang waktu dan bernilai tetap lainnya untuk selang waktu lain [5], yang salah satu contohnya diberikan dalam Gambar 3.
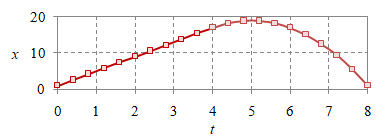 |
$x = \left\{\begin{array}{rr} 4t + 1, & 0 \le t < 4, \newline -2t^2 + 20t - 31, & 4 \le t < 8, \end{array}\right.$ |
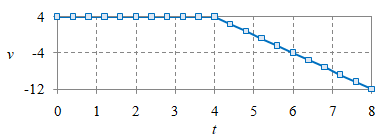 |
$v = \left\{\begin{array}{rr} 4, & 0 \le t < 4, \newline -4t + 20, & 4 \le t < 8, \end{array}\right.$ |
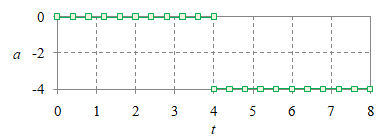 |
$a = \left\{\begin{array}{rr} 0, & 0 \le t < 4, \newline -4, & 4 \le t < 8, \end{array}\right.$ |
Gambar 3. Grafik posisi $x$ (atas), kecepatan $v$ (tengah), dan percepatannya $a$ (bawah) suatu gerak konsekutif dengan dua nilai percepatan.
Untuk gerak konsekutif yang lebih rumit misalnya dengan tiga nilai percepatan atau lebih, dapat dikonstruksi dengan cara yang sama.
position • position velocity • velocity acceleration