Hukum II Newton sebenarnya melibatkan hukum I Newton tanpa secara eksplisit dinyatakan, di mana hukum II ini merupakan bentuk yang lebih umumnya dari hukum I [1]. Salah satu yang sering menjadi sumber permasalah dalam memahami hukum ini adalah suku $F = ma$ dianggap sebagai suatu gaya dan bukan jumlah gaya-gaya [2].
Hukum II Newton menyatakan [3, 4, 5, 6]
Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.
sebagaimana bersumber dari text aslinya dan terdapat [7]
The alteration of motion is ever proportional to the motive force impressed; and is made in the direction of the right line in which that force is impressed.
merupakan terjemahan standar pertama, yang sampai saat ini, di tahun 2021, masih menarik untuk membahas pengubahan terjemahannya [8].
Saat ini umumnya hukum II Newton berbunyi [9]
A body acted upon by a force moves in such a manner that the time rate of change of momentum equals the force.
yang dapat diterjemahkan menjadi
Sebuah benda yang karena suatu gaya bergerak sedemikian rupa sehingga laju perubahan momentum terhadap waktu sama dengan gaya.
Pernyataan ini dapat diekspresikan dalam bentuk
\begin{equation}\label{eqn-newtons-laws-of-motion-2nd} \vec{F}_{\rm net} = \frac{d\vec{p}}{dt}, \end{equation}
dengan $\vec{F}_{\rm net}$ adalah jumlah semua gaya yang bekerja pada benda, $\vec{p}$ momentum linier, dan $t$ waktu.
Dengan menggunakan hukum II Newton permasalahan gerak benda secara umum dapat dirumuskan seberapa pun jumlah gaya yang berkerja pada suatu benda, walaupun belum tentu persamaan geraknya dapat dipecahkan.
Dekat dengan permukaan bumi gaya gravitasi dituliskan sebagai
\begin{equation}\label{eqn-force-gravitational} \vec{F}_G = m \vec{g}, \end{equation}
dengan $m$ massa dan $\vec{g}$ percepatan gravitas.
Benda berbentuk bola yang bergerak dalam fluida akan mengalami gaya gesek berbentuk
\begin{equation}\label{eqn-force-drag} \vec{F}_D = -6\pi R \eta (\vec{v} - \vec{u}), \end{equation}
dengan $D$ diameter benda, $\eta$ viskositas fluida, $\vec{v}$ kecepatan benda, dan $\vec{u}$ kecepatan fluida.
Benda yang tercelup dalam fluida akan mengalami gaya angkat fluida atau gaya Archimedes
\begin{equation}\label{eqn-force-buoyant} \vec{F}_A = -\rho V \vec{g}, \end{equation}
yang arahnya berlawanan dengan arah gravitasi $\vec{g}$, di mana $\rho$ massa jenis fluida, dan $V$ volume benda yang tercelup dalam fluida.
Benda bermuatan akan mengalami gaya listrik
\begin{equation}\label{eqn-force-electric} \vec{F}_E = q \vec{E}, \end{equation}
dengan $q$ muatan benda dan $\vec{E}$ medan listrik.
Dalam ruang bermedan magnetik benda bermuatan yang bergerak akan dipengaruhi gaya magnetik berbentuk
\begin{equation}\label{eqn-force-magnetic} \vec{F}_B = q \vec{v} \times \vec{B}, \end{equation}
dengan $q$ muatan benda, $\vec{v}$ kecepatan benda, dan $\vec{B}$ medan magnetik.
Benda yang terikat pegas akan mengalami gaya pegas
\begin{equation}\label{eqn-force-spring} \vec{F}_S = -k \left( \left| \vec{r} - \vec{o} \right| - L \right) \frac{\vec{r} - \vec{o}}{\left| \vec{r} - \vec{o} \right|}, \end{equation}
dengan $k$ konstanta pegas, $L_0$ panjang normal pegas dan $\vec{o}$ posisi ujung pegas tertambatkan, serta $\vec{r}$ posisi benda.
Dalam sebuah sistem, belum tentu sistem seperti ini ada dalam keadaan sebenarnya ![]() , sebuah benda mengalami berbagai gaya seperti pada Gambar berikut ini.
, sebuah benda mengalami berbagai gaya seperti pada Gambar berikut ini.
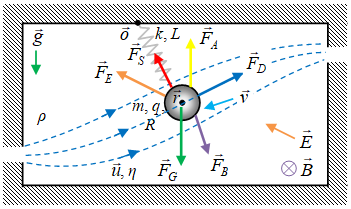
Gambar 1. Sebuah benda mengalami berbagai gaya dalam suatu sistem yang dibuat-buat.
Hukum II Newton untuk benda pada Gambar 1 adalah
\begin{equation}\label{eqn-force-many-forces} \begin{array}{rcl} m \vec{a} & = & \sum \vec{F} \newline & = & \vec{F}_A + \vec{F}_B + \vec{F}_D + \vec{F}_E + \vec{F}_G + \vec{F}_S \newline & = & -\rho V \vec{g} + q \vec{v} \times \vec{B} - 6\pi R \eta (\vec{v} - \vec{u}) \newline && \displaystyle + q \vec{E} + m \vec{g} - k \left( \left| \vec{r} - \vec{o} \right| - L \right) \frac{\vec{r} - \vec{o}}{\left| \vec{r} - \vec{o} \right|} \newline \displaystyle m \frac{d^2\vec{r}}{dt^2} & = & (m -\rho V) \ \vec{g} + q \ (\vec{E} + \vec{v} \times \vec{B}) + 6\pi R \eta \vec{u} \newline && \displaystyle - 6\pi R \eta \vec{v} - k \left( \left| \vec{r} - \vec{o} \right| - L \right) \frac{\vec{r} - \vec{o}}{\left| \vec{r} - \vec{o} \right|}, \end{array} \end{equation}
merupakan suatu persamaan suatu persamaan diferensial orde dua dan non-linier yang (mungkin) dapat dipecahkan. Penulisan Perasamaaan \eqref{eqn-force-many-forces} dapat disederhakanan menjadi
\begin{equation}\label{eqn-force-many-forces-simplified} \frac{d^2\vec{r}}{dt^2} = \vec{f}_0 + \vec{f}_1(\vec{r}) + \vec{f}_2(\vec{v}), \end{equation}
dengan menyembunyikan kerumitannya dalam
\begin{equation}\label{eqn-force-many-forces-simplified-f0} \vec{f}_0 = (m -\rho V) \ \vec{g} + q \ (\vec{E} + \vec{v} \times \vec{B}) + 6\pi R \eta \vec{u}, \end{equation}
yang berupa fungsi konstan,
\begin{equation}\label{eqn-force-many-forces-simplified-f1} \vec{f}_1(\vec{r}) = -k \left( \left| \vec{r} - \vec{o} \right| - L \right) \frac{\vec{r} - \vec{o}}{\left| \vec{r} - \vec{o} \right|}, \end{equation}
yang merupakan fungsi dari posisi benda $\vec{r}$, dan
\begin{equation}\label{eqn-force-many-forces-simplified-f2} \vec{f}_2(\vec{v}) = -6\pi R \eta \vec{v}, \end{equation}
yang merupakan fungsi dari kecepatan benda $\vec{v}$.
Bila tidak ada pegas berkonstanta $k$ dan medan magnetik $\vec{B}$ maka Persamaan \eqref{eqn-force-many-forces} akan menjadi
\begin{equation}\label{eqn-force-many-forces-k=0-B=0} m \frac{d\vec{v}}{dt} = \vec{c}_0 + c_1 \vec{v} \end{equation}
dengan
\begin{equation}\label{eqn-force-many-forces-k=0-B=0-c0} \vec{c}_0 = \left(1 - \frac{\rho V}{m} \right) \vec{g} + \left( \frac{q}{m} \right) \vec{E} + \left( \frac{6\pi R \eta}{m} \right) \vec{u}, \end{equation}
\begin{equation}\label{eqn-force-many-forces-k=0-B=0-c1} c_1 = - \frac{6\pi R \eta}{m}. \end{equation}
Perhatikan bahwa Persamaan \eqref{eqn-force-many-forces-k=0-B=0} merupakan persamaan diferensial orde pertama tidak homogen linier [10], yang kerumitannya terletak pada konstanta $\vec{c}_0$ saat akan diserap oleh $\vec{v}$, sehingga dapat memberikan persamaan diferensial orde pertama homogen linier [11], agar lebih mudah dipecahkan.
Secara umum Persamaan \eqref{eqn-force-many-forces-simplified} dapat dipecahkan dengan menggunakan metode numerik. Salah satu metode yang dapat digunakan adalah metode Euler[11], yang memungkin Persamaan \eqref{eqn-force-many-forces-simplified} dipecahkan menjadi beberapa baris persamaan numerik
\begin{equation}\label{eqn-force-many-forces-numerical} \begin{array}{rcl} \vec{a}_i & = & \vec{f}_0 + \vec{f}_1(\vec{r}_i) + \vec{f}_2(\vec{v}_i), \newline \vec{v} _{i+1} & = & \vec{v}_i + \vec{a}_i \ \Delta t, \newline \vec{r} _{i+1} & = & \vec{r}_i + \vec{v}_i \ \Delta t, \newline t _{i + 1} & = & t_i + \Delta t, \newline i & = & i + 1, \end{array} \end{equation}
yang dimulai dengan $i = 0$ dan syarat awal $\vec{r}_0 = \vec{r}(0)$ dan $\vec{v}_0 = \vec{v}(0)$ serta $t_0 = 0$. Secara iteratif dengan memiliki langkah waktu $\Delta t$ cukup kecil dalam meneksekusi Persaamaan \eqref{eqn-force-many-forces-numerical}, akan diperoleh solusi numerik dari Persamaan \eqref{eqn-force-many-forces-simplified}.
uniform linear motion • nonuniform linear motion • newton’s laws of motion • newton’s 1st law