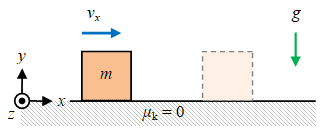
Gambar 1. Benda bergerak di atas permukaan mendatar tanpa gesekan, $\mu_k = 0$.
Hukum I Newton yang dirintis oleh Galileo dikenal pula sebagai hukum inersia, yang merupakan suatu lompatan konsep walaupun saat itu Galileo belum dapat melakukan observasi tanpa adanya gesekan, di mana konsep ini memperbaiki formulasi Aristoteles yang menyatakan bahwa bila ada gerak haruslah ada gaya luar yang menghasilkan gerak tersebut [1].
Newton’s first law termasuk ke dalam semantik produktif, di mana setiap generasi membaca dan menemukan pengertiannya, semakin kita mendalami proses mempelajari hukum ini, semakin banyak arti dan aspek yang terungkap, yang teks aslinya adalah
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
dengan
Every body perseveres in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed thereon.
adalah salah satu terjemahannya [2].
Hukum I newton yang menyatakan [3]
An object will remain at rest or in uniform motion in a straight line unless acted upon by an external force
yang dapat diterjemahkan menjadi
Sebuah benda akan berada dalam keadaan diam atau bergerak lurus dengan kecepatan tetap kecuali ada gaya luar yang bekerja padanya.
Pernyataan di atas dapat dituliskan dalam bentuk [4]
\begin{equation}\label{eqn-newtons-laws-of-motion-1st} \vec{F}_{\rm net} = 0 \Leftrightarrow \frac{d\vec{v}}{dt} = 0, \end{equation}
dengan $\vec{F}_{\rm net}$ adalah jumlah semua gaya yang bekerja pada benda, $\vec{v}$ adalah kecepatan, dan $t$ adalah waktu.
Sebuah benda yang bergerak pada permukaan horisontal tanpa gesekan merupakan contoh yang baik untuk pemanfaatan hukum I Newton. Sumbu $x$ pada arah horisontal dan positif ke kiri, sementara sumbu $y$ pada arah vertikal dan positif ke atas, sehingga percepatan gravitasi $g$ akan berlawan arah dengan aray $y$.

Gambar 1. Benda bergerak di atas permukaan mendatar tanpa gesekan, $\mu_k = 0$.
Sebuah benda bermassa $m$ bergerak di atas permukaan mendatar licin, $\mu_k = 0$, dengan kecepatan mendatar $v_x$ seperti pada Gambar 1 di atas. Sebenarnya hal ini merupakan permasalahan 2d akan tetapi menjadi 1d karena benda, kebetulan, diam pada arah vertikal atau arah $y$. Lalu terdapat syarat awal, mungkin akan terbaca secara sama-samar, bahwa $v_{0x} = v_x$ dan $v_{0y} = 0$.
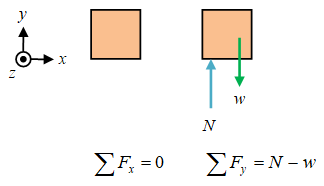
Gambar 2. Jumlah gaya-gaya pada arah: $x$ (kiri) dan $y$ (kanan).
Pada arah $x$ tidak terdapat gaya luar pada benda sehingga terpenuhi
\[\sum F_x = 0\]yang merupakan hukum I Newton. Dan karena syarat awalnya adalah $v_{0x} = v_x$ maka benda akan tetapi bergerak dengan kecepatan konstan $v_x$, seharusnya selamanya. Sedangkan untuk arah $y$
\[\sum F_y = N - w,\]di mana $N$ akan selalu menyeimbangi $w$ sampai permukaannya rusak atau ditembus benda karena besarnya gaya berat benda. Dengan demikian akan diperoleh juga $\sum F_y = 0$. Dikarenakan sejak awal benda diam pada permukaan mendatar licin atau $v_{0y} = 0$, maka seterusnya benda akan tetap diam.
Jadi pada contoh ini kedua keadaan awal pada hukum I Newton telah digunakan, yaitu bahwa benda yang semula diam akan tetap diam, dan benda yang semula bergerak dengan kecepatan tertentu akan tetap bergerak dengan kecepatan tersebut, selama tidak ada gaya luar (atau jumlah gaya luar adalah nol) yang bekerja pada benda.
Terdapat sistem benda yang bergerak turun pada suatu bidang miring kasar. Sudut kemiringan telah diatur sehingga gaya gesek kinetis dan gaya gravitasi yang sejajar bidang miring bernilai sama, yang menghasilkan jumlah gaya nol pada arah tersebut.
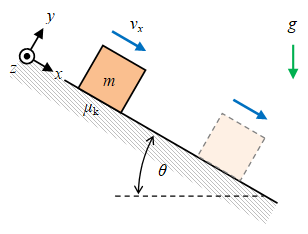
Gambar 3. Pada suatu bidang miring kasar $\mu_k = \tan \theta$, dengan sudut kemiringan $\theta$ terhadap arah mendatar, turun sebuah benda bermassa $m$ dengan kecepatan tetap $v_x$ menurut kerangka acuan di sebelah kiri atas.
Bila diatur agar $\tan\theta = \mu_k$ dan benda diberikan kecepatan awal tertentu, dalam hal ini $v_{0x} = v_x$, maka akan terjadi gerak dengan kecepatan tetap atau GLB (gerak lurus beraturan) pada arah $x$. Pada arah $y$ benda diam atau $v_{0y} = 0$.
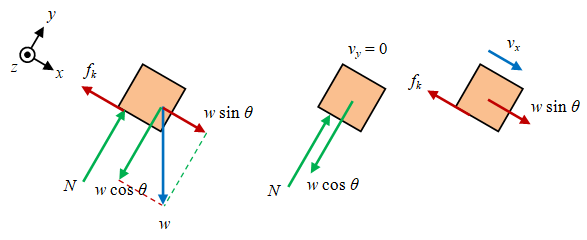
Gambar 4. Diagram gaya arah $x$ dan $y$ pada benda yang turun dengan kecepatan tetap pada bidang miring kasar.
Pada arah $y$ gaya normal $N$ dari bidang miring ke benda selalu menyeimbangi $w \cos\theta$ sehingga
\[\begin{array}{rcl} \sum F_y & = & N - w \cos \theta \newline 0 & = & N - w \cos \theta \newline N & = & w \cos \theta \newline & = & mg \cos \theta. \end{array}\]Selain bahwa benda tidak bergerak pada arah $y$ karena $v_{0y} = 0$, hasil ini kemudian digunakan untuk menghitung gaya gesek kinetik
\[\begin{array}{rcl} f_k & = & \mu_k \ N \newline & = & \mu_k \ mg \cos \theta, \end{array}\]yang dengan $\mu_k = \tan \theta$ akan menjadi
\[\begin{array}{rcl} f_k & = & \mu_k \ mg \cos \theta \newline & = & (\tan \theta) \ mg \cos \theta \newline & = & mg \sin \theta. \end{array}\]Hasil gaya gesek kinetis $f_k$ ini kemudian digunakan pada
\[\begin{array}{rcl} \sum F_x & = & m a_x \newline mg\sin\theta - f_k & = & m a_x \newline mg\sin\theta - mg\sin\theta & = & m a_x \newline 0 & = & m a_x \newline a_x & = & 0 \end{array}\]yang membuat benda ber-GLB pada arah $x$. Dengan demikian benda akan selalu bergerak dengan $v_x$ karena kecepatan awalnya adalah $v_{0x} = v_x$ dan $a_x = 0$.
Saat benda yang jatuh akibat gaya beratnya sambil dipengaruhi oleh gaya angkat fluida dan gesekan udara mencapai kecepatan terminalnya merupakan suatu contoh lain dari penerapan hukum I Newton. Saat itu gaya gravitasi telah diimbangi oleh gaya Archimedes dan gaya gesek udara [4].
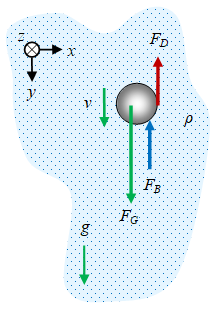
Gambar 5. Benda jatuh karena gaya gravitasi $F_G$ yang diimbangi oleh gaya apung $F_B$ dan gaya gesek udara $F_D$, dengan massa jenis udara $\rho$ dan percepatan gravitasi $g$.
Persamaan gerak benda pada arah $y$ pada Gambar 5 adalah
\begin{equation}\label{eqn-fall-buoyancy-air-resistance-motion} \begin{array}{rcl} m a & = & \sum F_y \newline & = & F_G - F_B - F_D \newline & = & mg - \rho V g - \tfrac12 \rho A C_d \ v^2 \newline m a + \tfrac12 \rho A C_d \ v^2 + \rho V g - mg & = & 0 \newline \displaystyle a + \left( \frac{\rho A C_d}{2m} \right) v^2 + \left( \frac{\rho V g}{m} - g \right) & = & 0 \newline \displaystyle \frac{dv}{dt} + \left( \frac{\rho A C_d}{2m} \right) v^2 + \left( \frac{\rho V g}{m} - g \right) & = & 0, \end{array} \end{equation}
dengan mengambil arah positif $y$ searah gerak, yaitu searah percepatan gravitasi $g$. Persamaan \eqref{eqn-fall-buoyancy-air-resistance-motion} merupakan persamaan diferensial non-linier yang harus dipecahkan untuk mendaptkan solusi $v = v(t)$. Untuk keadaan kecepatan terminal tercapai $a = 0$ dan $v = v_\infty$ sehingga dari Persamaan \eqref{eqn-fall-buoyancy-air-resistance-motion} akan memberikan
\begin{equation}\label{eqn-fall-buoyancy-air-resistance-motion-vterm} \begin{array}{rcl} m a & = & \sum F_y \newline & = & F_G - F_B - F_D \newline & = & mg - \rho V g - \frac12 \rho A C_d \ v^2 \newline m \cdot 0 & = & mg - \rho V g - \frac12 \rho A C_d \ v_\infty^2 \newline 0 & = & mg - \rho V g - \frac12 \rho A C_d \ v_\infty^2 \newline \frac12 \rho A C_d \ v_\infty^2 & = & mg - \rho V g \newline & = & (m - \rho V) g \newline v_\infty^2 & = & \displaystyle \frac{2 (m - \rho V) g}{\rho A C_d} \newline v_\infty & = & \displaystyle \sqrt{\frac{2 (m - \rho V) g}{\rho A C_d}}, \end{array} \end{equation}
percepatan terminal yang dicari.
Massa yang tergantung sambil ditarik oleh suatu gaya tetap serta terimbangi oleh tali lain sehingga benda dalam keadaan diam, juga merupakan penerapan dari hukum I Newton. Salah satu contohnya diberikan pada Gambar 6 berikut.
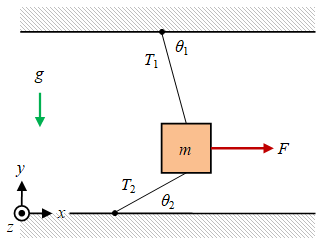
Gambar 6. Sebuah benda bermassa $m$ tergantung oleh tegangan tali $T_1$ dan ditarik oleh gaya $F$ secara mendatar serta ditahan agar setimbang oleh tegangan tali $T_2$, dengan masing-masing tali memiliki sudut $\theta_1$ dan $\theta_2$ terhadap arah mendatar dan percepatan gravitasi $g$ mengarah ke bawah.
Gaya-gaya yang bekerja pada benda dapat digambarkan sebagaimana diberikan pada Gambar 7 di bawah ini.
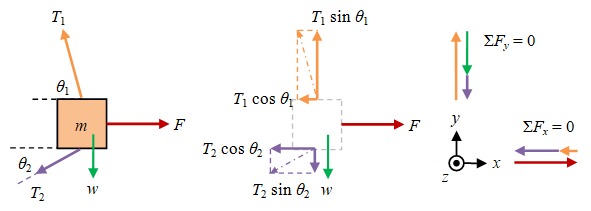
Gambar 7. Gaya-gaya yang bekerja pada benda (kiri), uraian gaya-gaya pada arah $x$ dan $y$ (tengah), dan penjumlahan gaya pada setiap arah diperoleh nol.
Dengan mengambarkan diagram gaya pada benda bermassa $m$ dapat diperiksa apakah semua gaya yang berperan telah dipertimbangkan. Selanjutnya adalah menentukan arah-arah di mana gaya-gaya tertentu perlu diproyeksikan. Untuk kasus ini tela dipilih arah $x$ dan $y$, di mana proyeksi gaya-gaya pada kedua arah tersebut dapat dilihat pada Gambar 7 (tengah), kemudian menunjukkan bahwa secara ilustratif jumlah gaya-gaya pada kedua araha adalah nol sebagaimana diberikan pada Gambar 7 (kanan).
Sistem-sistem yang telah dibahas sebelumnya dibandingkan sebagai berikut ini.
Tabel 1. Perbandingan beberapa sistem sebagai contoh penerapan hukum I Newton.
| Gambar | Nama | arah $x$ | arah $y$ |
|---|---|---|---|
| 1 | frictionless horizontal surface | $\sum F_x = 0$, $v_{x0} = v_x$ |
$\sum F_y = 0$, $v_{y0} = 0$ |
| 3 | incline with friction | $\sum F_x = 0$, $v_{x0} = v_x$ |
$\sum F_y = 0$, $v_{y0} = 0$ |
| 5 | falling with air resistance | $\sum F_x = 0$, $v_{x0} = 0$ |
$\sum F_y = 0$, $v_{y0} = 0$, $v_\infty \ne 0$ |
| 6 | hanging mass | $\sum F_x = 0$, $v_{x0} = 0$ |
$\sum F_y = 0$, $v_{y0} = 0$ |
Saat berlakunya hukum I Newton benda akan diam atau ber-GLB (gerak lurus beraturan) dan hal ini terlihat pada $v = v_0$ untuk sistem pada baris pertama, kedua, dan keempat pada Tabel 1. Pengecualian terdapat untuk sistem pada baris ketiga, di mana $v_{0y} = 0$ akan tetapi $v_\infty \ne v_{0y}$ karena kecepatan sempat bertambah dan kemudian menjadi konstan. Jadi GLB tercapai setelah beberapa saat, bukan sejak awal untuk sistem ini, tidak seperti pada sistem-sistem lainnya.
uniform linear motion • nonuniform linear motion • newton’s laws of motion