uniform linear motion

Gerak lurus merupakan gerak dari obyek yang mengikuti suatu garis lurus dan beraturan, dalam hal ini, berarti percepatan bernilai nol selama benda bergerak. Dengan demikian gerak lurus beraturan atau GLB merupakan gerak benda mengikuti lintasan lurus dengan kecepatan tetap atau beraturan atau seragam [1]. GLB ini merupakan salah satu bagian dari gerak lurus, di mana bagian lainnya adalah gerak lurus dengan percepatan berubah [2].

equations

Terdapat beberapa persamaan untuk GLB, yaitu

$$\begin{equation}\label{eqn-uniform-linear-motion-1} a = 0, \end{equation}$$

$$\begin{equation}\label{eqn-uniform-linear-motion-2} v = v_0, \end{equation}$$

$$\begin{equation}\label{eqn-uniform-linear-motion-3} x = x_0 + v_0 t, \end{equation}$$

dengan $a$ percepatan, $v_0$ kecepatan awal, $v$ kecepatan setiap saat, $x_0$ posisi awal, $x_0$ posisi setiap saat, dan $t$ waktu. Persamaan $\eqref{eqn-uniform-linear-motion-1}$ dan $\eqref{eqn-uniform-linear-motion-2}$ umumnya tidak dituliskan karena dianggap sudah dipahami dan Persamaan $\eqref{eqn-uniform-linear-motion-3}$ lebih sering dituliskan sebagai

$$\begin{equation}\label{eqn-uniform-linear-motion-3b} x = v t, \end{equation}$$

dengan $\Delta x = x - x_0 \equiv x$ perpindahan, $v$ kecepatan, dan $t$ waktu. Semua $t$ di atas sebenarnya lebih tepat bila dituliskan sebagai $\Delta t = t - t_0$ yang menggambarkan selang waktu, akan tetapi penulisan dengan $t$ sudah menjadi umum dan terlihat lebih sederhana [3]. Jadi, penyederhanaan penulisan pada Persamaan $\eqref{eqn-uniform-linear-motion-3b}$ telah terdapat asumsi bahwa gerak dimulai pada posisi $x_0 = 0$ dan saat $t_0 = 0$. Hal ini menjadi penting saat akan merangkai beberapa GLB dalam suatu gerak konsekutif.

graphics

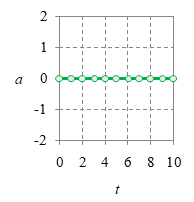
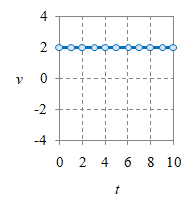
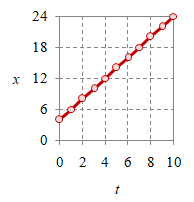
Untuk variabel kinematika $x$, $v$, $a$ dapat digambarkan grafiknya sebagai fungsi waktu $t$ sebagai berikut ini.

Gambar 1. Grafik $a-t$ (kiri), $v-t$ (tengah), dan $x-t$ (kanan).

Ilustrasi grafik suatu GLB diberikan pada Gambar 1 untuk $x = 4 + 2t$, $v = 2$, dan $a = 0$. Untuk kasus GLB ini percepatan akan selalu bernilai nol, sedangkan posisi $x$ dan $v$ terhubung melalui Persamaan $\eqref{eqn-uniform-linear-motion-3b}$ atau yang lebih umum

$$\begin{equation}\label{eqn-uniform-linear-motion-3c} x = \int v \ dt, \end{equation}$$

yang akan menjadi

$$\begin{equation}\label{eqn-uniform-linear-motion-3d} \Delta x = x - x_0 = \int_{t_0}^t v \ dt, \end{equation}$$

bila diberi batas bawah dan atas integral, dengan syarat awal $x_0 = x(t_0)$. Persaamaan $\eqref{eqn-uniform-linear-motion-3c}$ dan $\eqref{eqn-uniform-linear-motion-3d}$ menghitung luas di bawah kurva, yang untuk suatu GLB menjadi sederhana karena kurva $v$ merupakan garis mendatar.

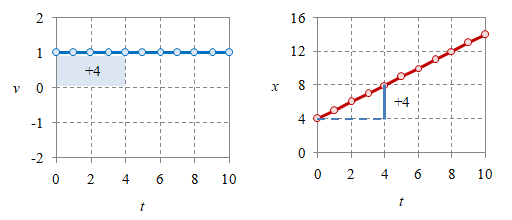
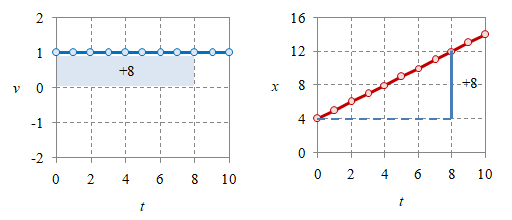
Gambar 2. Luas di bawah kurva kecepatan $v$: $t_0 = 0$, $t = 4$ memberikan luas $4$ (atas) dan $t_0 = 0$, $t = 8$ memberikan luas $8$ (bawah).

Sebagai ilustrasi batas bawah integral adalah $t_0 = 0$ dan batas atasnya adalah $t = 4$ yang memberikan luas $A \equiv \Delta x = 4$ dan nilai ini setelah ditambahkan pada posisi awal $x_0 = 4$ akan menghasilkan posisi $x = 8$ sebagaimana ditunjukkan pada Gambar 2 (atas). Kemudian dengan mengubah batas atasnya menjadi $t = 8$ akan diperoleh luas di bawah kurva luas $A \equiv \Delta x = 4$ dan dengan menambahkan nilai ini pada posisi awal $x_0 = 4$ akan menghasilkan posisi akhir $x = 12$ seperti diberikan pada Gambar 2 (bawah).

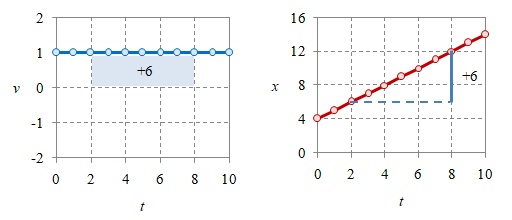
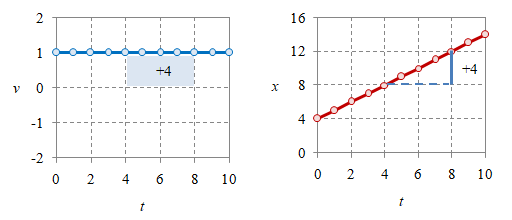
Gambar 3. Luas di bawah kurva kecepatan $v$: $t_0 = 2$, $t = 8$ memberikan luas $6$ (atas) dan $t_0 = 4$, $t = 8$ memberikan luas $4$ (bawah).

Integral dengan batas bawah dan atas yang diberikan oleh Persaamaan $\eqref{eqn-uniform-linear-motion-3d}$ merupakan luas di bawah kurva $A$ berupa perpindahan $\Delta x$. Dengan demikian, perpindahan $\Delta x$ tidak bergantung posisi awal $x_0$, akan tetapi sebaliknya

$$\begin{equation}\label{eqn-uniform-linear-motion-4} x = x_0 + \Delta x \end{equation}$$

posisi akhir $x$ yang bergantung posisi awal $x_0$ ini dan perpindahannya $\Delta x$.

1d motion

Gerak lurus merupakan gerak 1d, yang belum tentu harus dalam arah $x$. Bisa saja dalam arah $y$, $z$, atau arah lainnya asalkan berupa garis lurus.

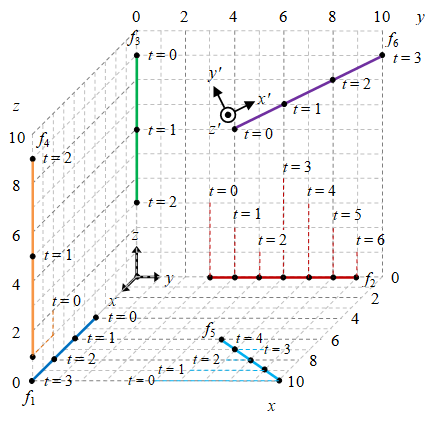
Gambar 4. Beberapa lintasan benda yang ber-GLB dalam ruang 3d, di mana masing-masing lintasan berupa garis lurus.

Pada Gambar 4 terdapat lima lintasan benda ber-GLB, yaitu $f_1$, $f_2$, $f_3$, $f_4$, dan $f_5$. Semuanya merupakan garis lurus akan tetapi tidak hanya $x$ fungsi dari $t$, melainkan dapat pula berupa $y$, $z$, atau lainnya. Lintasan pertama $f_1$ dapat direpresentasikan dengan

$$\begin{equation}\label{eqn-line-3d-f1} f_1 = \left\{ \begin{array}{l} x = 4 + 2t, \newline y = 0, \newline z = 0, \newline 0 \le t \le 3, \end{array} \right. \end{equation}$$

di mana untuk kasus pada ruang 1d hanya baris pertama (dan terakhir) yang dibutuhkan. Untuk $f_2$, $f_3$, dan $f_4$ berlaku cara yang sama.

exer

1. Sebuah benda bergerak di sepanjang sumbu $x$ dengan kecepatan tetap $2 \ \rm m/s$ ke arah kanan menuju $+x$. Saat $t = 0 \ \rm s$ benda berada posisi $x = 4$. Tentukan posisi benda saat $t = 3 \ \rm s$ dan $t = 5 \ \rm s$.
2. Saat $t = 4 \ \rm s$ benda yang ber-GLB berada pada posisi $x = 6 \ \rm m$ dan $t = 8 \ \rm s$ berada pada posisi $x = 2 \ \rm m$. Hitunglah kecepatan benda.
3. Dengan menggunakan Gambar 4 tuliskanlah lintasan kedua $f_2$.
4. Carilah lintasan ketiga $f_3$ pada Gambar 4.
5. Tuliskan lintasan keempat $f_4$ yang terdapat pada Gambar 4.

note

1. -, “Uniform Linear Motion” in College Physics, Physics, LibreText, 31 Dec 2020, url https://phys.libretexts.org/@go/page/31883 [20211024].
2. Wikipedia contributors, “Linear motion”, Wikipedia, The Free Encyclopedia, 31 August 2021, 01:12 UTC, url https://en.wikipedia.org/w/index.php?oldid=1041524488 [20211024].
3. -, “What are the kinematic formulas?”, Khan Academy, url https://www.khanacademy.org/science/physics/one-dimensional-motion/kinematic-formulas/a/what-are-the-kinematic-formulas [20211024].

position • velocity • velocity acceleration • position velocity • kinematics equations 1d