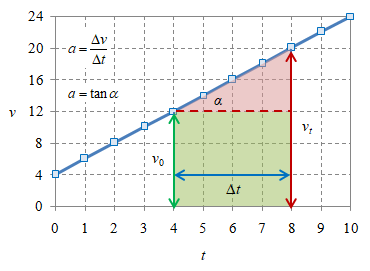
Gambar 1. Hubungan antara kecepatan awal $v_0$, kecepatan akhir $v_t$, selang waktu $\Delta t$, dan percepatan $a$.
Gerak lurus berubah beraturan atau GLBB adalah gerak dengan percepatan konstan, baik besar maupun arahnya [1], yang besarnya percepatan dapat bernilai positif ataupun negatif (bukan nol) [2], di mana gerak ini merupakan salah satu dari dua jenis gerak linier [3]. Terdapat pula nama lainnya yaitu gerak lurus dengan percepatan [4].
Kecepatan benda yang ber-GLBB akan berubah dari kecepatan awal $v_0$ menjadi kecepatan akhir $v_t$ pada saat waktu $t$ mengikuti
\begin{equation}\label{eqn-nonuniform-linear-motion-v} v_t = v_0 + at, \end{equation}
dengan $a$ merupakan percepatan konstan.

Gambar 1. Hubungan antara kecepatan awal $v_0$, kecepatan akhir $v_t$, selang waktu $\Delta t$, dan percepatan $a$.
Untuk gerak dengan percepatan konstan sebagaimana suatu GLBB, percepatan $a$ dapat diperoleh dengan cara menghitung percepatan rata-rata
\begin{equation}\label{eqn-nonuniform-linear-motion-a} a \equiv a_{\rm avg} = \frac{\Delta v}{\Delta t}, \end{equation}
yang dalam Gambar 1 merupakan kemiringan garis atau $\tan \alpha$. Dengan demikian
\begin{equation}\label{eqn-nonuniform-linear-motion-a-v} \begin{array}{rcl} \displaystyle \frac{v_t - v_0}{\Delta t} & = & a \newline v_t - v_0 & = & a \Delta t, \newline v_t & = & v_0 + a \Delta t, \end{array} \end{equation}
yang tak lain merupakan Persamaan \eqref{eqn-nonuniform-linear-motion-v} karena di sini $\Delta t \equiv t$ memang menggambarkan selang waktu, suatu kebiasaan yang telah umum [5]. Selanjutnya selain Persamaan \eqref{eqn-nonuniform-linear-motion-v} terdapat pula hubungan
\begin{equation}\label{eqn-nonuniform-linear-motion-x} \Delta x = v_0 t + \tfrac12 at^2, \end{equation}
yang merupakan luas di bawah kurva fungsi $v = v(t)$ seperti pada Gambar 1 melalui hubungan $x$ dan $v$ melalui integral. Luas di bawah kurva pada Gambar 1 dapat diperoleh dari luas daerah segiempat berwarna hijau dan segitiga berwarna merah
\[\begin{array}{rcl} A & = & A_\color{green}{\square} + A_\color{red}{\triangle} \newline & = & v_0 \Delta t + \frac12 \Delta t (v_t - v_0) \newline & = & v_0 \Delta t + \frac12 \Delta t (v_0 + a\Delta t - v_0) \newline & = & v_0 \Delta t + \frac12 \Delta t \ a \ \Delta t \newline & = & v_0 \Delta t + \frac12 a (\Delta t)^2, \end{array}\]dengan $A = \Delta x$ dan kembali $\Delta t \equiv t$ maka akan diperoleh Persamaan \eqref{eqn-nonuniform-linear-motion-x}.
Selain Persamaan \eqref{eqn-nonuniform-linear-motion-v} dan \eqref{eqn-nonuniform-linear-motion-x} terdapat pula hubungan
\begin{equation}\label{eqn-nonuniform-linear-motion-v-x-a} v_t^2 = v_0^2 + 2 a \Delta x. \end{equation}
Substitusi $t$ pada Persamaan \eqref{eqn-nonuniform-linear-motion-x} dengan $t$ dari Persamaan \eqref{eqn-nonuniform-linear-motion-v}
\[\require{cancel} \begin{array}{rcl} \Delta x & = & v_0 t + \frac12 a t^2 \newline & = & \displaystyle v_0 \left( \frac{v_t - v_0}{a} \right) + \frac12 a \left( \frac{v_t - v_0}{a} \right)^2 \newline & = & \displaystyle \frac{v_0 v_t - v_0^2}{a} + \frac{v_t^2 - 2v_0v_t + v_0^2}{2a} \newline & = & \displaystyle \frac{2v_0 v_t - 2v_0^2}{2a} + \frac{v_t^2 - 2v_0v_t + v_0^2}{2a} \newline 2a\Delta x & = & (2v_0 v_t - 2v_0^2) + (v_t^2 - 2v_0v_t + v_0^2) \newline 2a\Delta x & = & \cancel{2v_0 v_t} - 2v_0^2 + v_t^2 - \cancel{2v_0v_t} + v_0^2 \newline 2a\Delta x & = & - 2v_0^2 + v_t^2 + v_0^2 \newline 2a\Delta x & = & - v_0^2 + v_t^2 \newline v_0^2 + 2a\Delta x & = & v_t^2 \newline \end{array}\]akan memberikan Persamaan \eqref{eqn-nonuniform-linear-motion-v-x-a}. Selanjutnya adalah substitusi Persamaan \eqref{eqn-nonuniform-linear-motion-v} ke Persaamaan \eqref{eqn-nonuniform-linear-motion-x} hanya untuk suku $v_0$
\begin{equation}\label{eqn-nonuniform-linear-motion-v–at} \require{cancel} \begin{array}{rcl} \Delta x & = & v_0 t + \frac12 a t^2 \newline & = & (v_t - at) \ t + \frac12 a t^2 \newline & = & v_t t - at^2 + \frac12 a t^2 \newline & = & v_t t - \frac12 a t^2, \end{array} \end{equation}
yang merupakan persamaan kinematika lagi untuk GLBB yang dapat digunakan. Persamaan \eqref{eqn-nonuniform-linear-motion-x} dan \eqref{eqn-nonuniform-linear-motion-v–at} dapat dijumlahkan sehingga menghasilkan
\begin{equation}\label{eqn-nonuniform-linear-motion-x-v0-vt} \require{cancel} \begin{array}{rcl} 2 \Delta x & = & \Delta x + \Delta x \newline & = & (v_0 t + \frac12 a t^2) + (v_t t - \frac12 a t^2) \newline & = & v_0 t + \cancel{\frac12 a t^2} + v_t t - \cancel{\frac12 a t^2} \newline & = & (v_0 + v_t) t \newline \Delta x & = & \frac12 (v_0 + v_t) t, \end{array} \end{equation}
yang merupakan persamaan kinematika GLBB kelima yang juga dapat digunakan.
Tabel 1. Lima persaamaan kinematika untuk GLBB dengan variabel yang tidak perlu diketahuinya $\cancel{U}$.
| No | Persamaan | $\cancel{U}$ |
|---|---|---|
| \eqref{eqn-nonuniform-linear-motion-v} | $v_t = v_0 + at$ | $\Delta x$ |
| \eqref{eqn-nonuniform-linear-motion-x} | $\Delta x = v_0 t + \frac12 a t^2$ | $v_t$ |
| \eqref{eqn-nonuniform-linear-motion-v-x-a} | $v_t^2 = v_0^2 + 2a\Delta x$ | $t$ |
| \eqref{eqn-nonuniform-linear-motion-v–at} | $\Delta x = v_t t - \frac12 a t^2$ | $v_0$ |
| \eqref{eqn-nonuniform-linear-motion-x-v0-vt} | $\Delta x = \frac12 (v_0 + v_t) t$ | $a$ |
Saat memecahkan suatu permasalan kinematika dapat digunakan kelima persamaan dalam Tabel 1, yang masing-masing memiliki satu variabel kinematika yang tidak perlu diketahui $\cancel{U}$. Sebagai contoh bila tidak diketahui percepatan $a$ dan juga tidak ditanyakan, maka Persamaan \eqref{eqn-nonuniform-linear-motion-x-v0-vt} yang digunakan.
Sebuah benda yang memiliki percepatan konstan $1 \ \rm m/s^2$ bergerak lurus dengan kecepatan awal $3 \ \rm m/s$. Bila saat ini kecepatannya adalah $5 \ \rm m/s$ berapakah perpindahan yang telah ditempuhnya?
Pada permasalahan di atas telah diketahui percepatan $a$, kecepatan awal $v_0$, kecepatan akhir $v_t$, dan ditanya perpindahan yang ditempuh $\Delta x$. Waktu $t$ sama sekali tidak disinggung, sehingga akan digunakan Persamaan \eqref{eqn-nonuniform-linear-motion-v-x-a} untuk menyelesaikannya.
Tabel 1 memberikan lima persamaan yang dapat digunakan untuk memecahkan permasalahan GLBB bila salah satu variabel kinematika tidak diketahui. Untuk sebuah contoh saja dapat dibuat variasi permasalahan sehingga harus dipecahkan oleh salah satu dari lima persamaan tersebut.
Sebuah benda ber-GLBB dengan percepatan $2 \ \rm m/s^2$ dan kecepatan awal $5 \ \rm m/s$. Tentukan kecepatan benda setelah $4 \ \rm s$.
Hitunglah perpindahan benda setelah $4 \ \rm s$ bila benda mulai bergerak dengan kecepatan awal $5 \ \rm m/s$ dan selama geraknya percepatannya bernilai konstan $2 \ \rm m/s^2$.
Sebuah benda yang bergerak lurus dengan percepatan tetap $2 \ \rm m/s^2$ berpindah sejauh $36 \ \rm m$. Berapakah kecepatan akhir benda bila kecepatan awalnya adalah $5 \ \rm m/s$?
Sebuah benda begerak lurus dengan percepatan tetap $2 \ \rm m/s^2$ bergerak dengan kecepatan awal tertentu selama $4 \ \rm s$ untuk menempuh jarak tertentu. Bila pada saat akhir diketahui kecepatannya adalah $13 \ \rm m/s$, tentukan jarak yang ditempuh benda.
Sebuah benda bergerak lurus dengan percepatan tetap menempuh suatu jarak tertentu selama $4 \ \rm s$. Bila saat awal dan akhir kecepatan benda diukur dengan menggunakan radar kecepatan portabel dan memberikan hasil $5 \ \rm m/s$ dan $13 \ \rm m/s$, berapakah jarak yang telah ditempuh benda?
Tabel 2. Lima persamaan kinematika dan lima variabel terkaitnya, serta variasi pertanyaan yang dapat dibuat. $\newcommand{\rlx}{\large\color{#c00}\times}$
| Persamaan | $v_0$ | $v_t$ | $a$ | $t$ | $\Delta x$ | Variasi |
|---|---|---|---|---|---|---|
| $v_t = v_0 + at$ | $5$ | $13$ | $2$ | $4$ | $\rlx$ | $4$ |
| $\Delta x = v_0 t + \frac12 a t^2$ | $5$ | $\rlx$ | $2$ | $4$ | $36$ | $4$ |
| $v_t^2 = v_0^2 + 2a\Delta x$ | $5$ | $13$ | $2$ | $\rlx$ | $36$ | $4$ |
| $\Delta x = v_t t - \frac12 a t^2$ | $\rlx$ | $13$ | $2$ | $4$ | $36$ | $4$ |
| $\Delta x = \frac12 (v_0 + v_t) t$ | $5$ | $13$ | $\rlx$ | $4$ | $36$ | $4$ |
Dengan demikian dengan hanya menggunakan lima variabel kinematika $v_0$, $v_t$, $a$, $t$, dan $\Delta x$ dapat dibuat sekitar
\[4 + 4 + 4 + 4 + 4 = 20\]variasi permasalahan. Sebagai contoh untuk baris pertama pada Tabel 2 empat variasi yang dimaksud adalah dapat ditanyakan $v_0$, $v_t$, $a$, dan $t$.
Dengan hubungan melalui integral dan diferensial antara $a$ dan $v$, serta $v$ dan $x$, dapat diberikan ilustrasi kurva antara ketiga variabel tersebut.
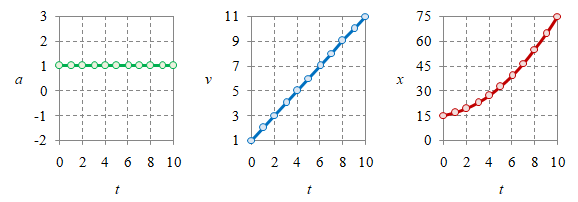
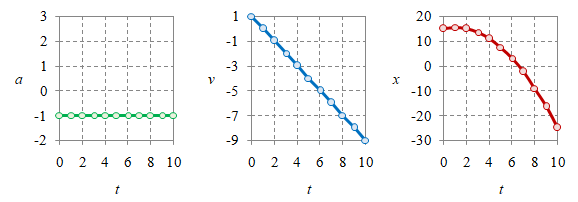
Gambar 2. Kurva percepatan $a$, kecepatan $v$, dan posisi $x$ untuk $a > 0$ (atas) dan $a < 0$ (bawah).
Pengaruh dari tanda percepatan $a$ bagi kecepatan $v$ dan posisi $x$ diberikan pada Gambar 2. Perhatikan bahwa paling mudah melihat pengaruhnya adalah pada kurva $v$ karena $a$ adalah kemiringan kurva atau gradiennya kurva $v$.
Tabel 3. Variasi tanda percepatan $a$, kecepatan awal $v$, dan posisi awal $x_0$ untuk suatu GLBB.
| ID | $a$ | $v_0$ | $x_0$ | ID | $a$ | $v_0$ | $x_0$ | ID | $a$ | $v_0$ | $x_0$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
0A |
$-$ | $-$ | $-$ | 0D |
$-$ | $0$ | $-$ | 0G |
$-$ | $+$ | $-$ |
0B |
$-$ | $-$ | $0$ | 0E |
$-$ | $0$ | $0$ | 0H |
$-$ | $+$ | $0$ |
0C |
$-$ | $-$ | $+$ | 0F |
$-$ | $0$ | $+$ | 0I |
$-$ | $+$ | $+$ |
| ID | $a$ | $v_0$ | $x_0$ | ID | $a$ | $v_0$ | $x_0$ | ID | $a$ | $v_0$ | $x_0$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
0K |
$+$ | $-$ | $-$ | 0N |
$+$ | $0$ | $-$ | 0Q |
$+$ | $+$ | $-$ |
0L |
$+$ | $-$ | $0$ | 0O |
$+$ | $0$ | $0$ | 0R |
$+$ | $+$ | $0$ |
0M |
$+$ | $-$ | $+$ | 0P |
$+$ | $0$ | $+$ | 0S |
$+$ | $+$ | $+$ |
Untuk suatu GLBB, di mana $a \ne 0$, saat dilakukan integral untuk untuk mendapatkan nilai $v$ dan $x$, dibutuhkan syarat awal berupa kecepatan awal $v_0$ dan posisi awal $x_0$. Tanda dari percepatan $a$, kecepatan awal $v$, dan posisi awal $x_0$ akan menentukan grafik-grafiknya, dengan variasi tanda yang mungkin telah diberikan pada Tabel 3.
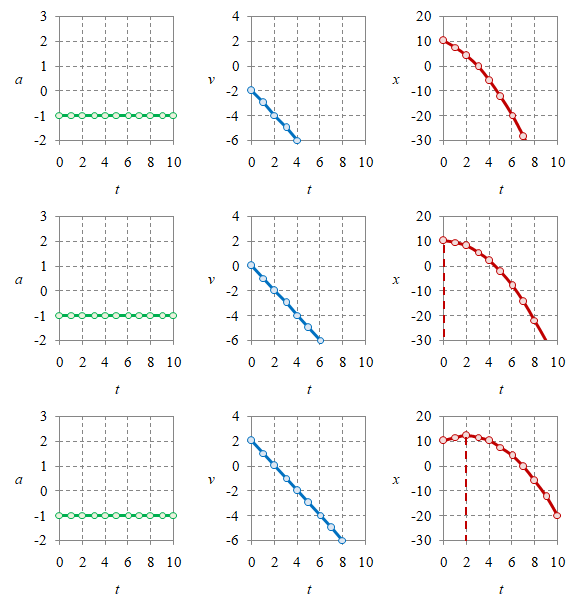
Gambar 3. Kurva percepatan $a$, kecepatan $v$, dan posisi $x$ untuk tanda [$a$, $v$, $x$, ID]: [$-$, $-$, $+$, 0C] (atas), [$-$, $0$, $+$, 0F] (atas), dan [$-$, $+$, $+$, 0I] (bawah).
Dengan $a < 0$ maka kurva $v$ akan berupa garis lurus miring ke bawah (gradien negatif) dan $v_0$ hanya menentukan titik potongnya pada sumbu vertikal. Untuk kurva $x$ terdapat peran $x_0$ yang juga menentukan titik potong dengan sumbu vertikal, sedang puncak kurva parabola ditentukan terdapat pada $t = - v_0 / a$.
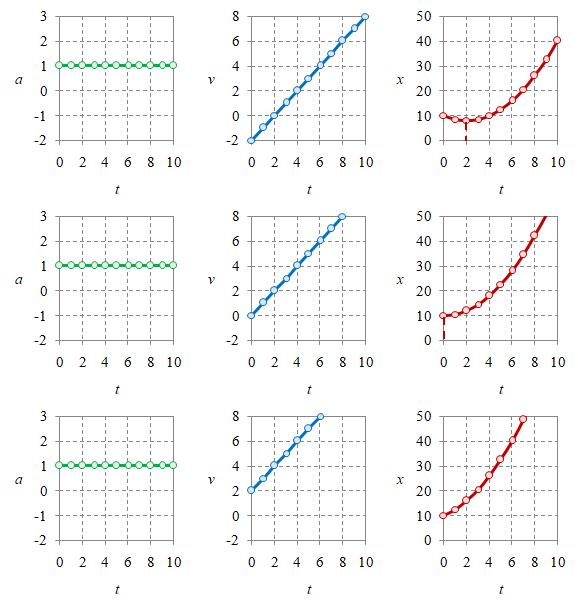
Gambar 4. Kurva percepatan $a$, kecepatan $v$, dan posisi $x$ untuk tanda [$a$, $v$, $x$, ID]: [$+$, $-$, $+$, 0M] (atas), [$+$, $0$, $+$, 0P] (atas), dan [$+$, $+$, $+$, 0S] (bawah).
Kurva $v$ akan berupa garis lurus miring ke atas (gradien positif) bila $a > 0$ dan $v_0$ hanya menentukan titik potongnya pada sumbu vertikal. Peran $x_0$ pada kurva $x$ adalah menentukan titik potong dengan sumbu vertikal, sedang puncak kurva parabola, seperti sebelumnya, ditentukan terdapat pada $t = - v_0 / a$.
Sebenarnya terdapat kurva-kurva lain dengan nilai $x_0$ yang berbeda, akan tetapi tidak ditampilkan karena dianggap cukup jelas bahwa nilai $x_0$ ini hanya menentukan titik potong pada sumbu vertikal atau menggeser kurva secara vertikal (ke atas untuk $x_0 > 0$ dan ke bawah untuk $x_0 < 0$).
position • velocity • velocity acceleration • position velocity • kinematics equations 1d • uniform linear motion