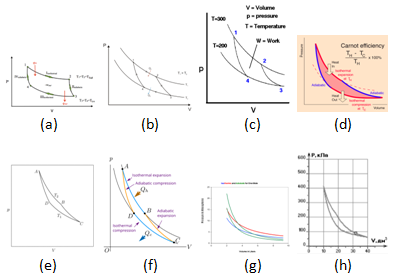
Gambar 1. Diagram siklus Carnot ilustratif: (a) [2], (b) [3], (c) [4], (d) [5]; semi realistik: (e) [6], (f) [7]; dan realistik: (g) [8], (h) [9].
Terdapat diskusi yang menggelitik mengenai representasi siklus Carnot, yaitu apakah diagram sebaiknya digambarkan hanya secara ilustratif atau sebaiknya sesuai dengan angka-angka sebenarnya [1]. Penelusuran menunjukkan bahwa terdapat berbagai gambar ilustratif [2, 3, 4, 5], semi-realistik [6, 7], dan realistik karena dihitung menggunakan angka, akan tetapi pada bagian penjelasannya tetap menggunakan diagram yang kurang realistik [8, 9].
Contoh-contoh diagram siklus Carnot yang bersifat ilustratif, semi-realistik, dan realistik diberikan di bawah ini.

Gambar 1. Diagram siklus Carnot ilustratif: (a) [2], (b) [3], (c) [4], (d) [5]; semi realistik: (e) [6], (f) [7]; dan realistik: (g) [8], (h) [9].
Sekilas dapat terlihat bahwa diagram ilustratif lebih mudah untuk dilihat ketimbang yang realistik. Pada diagram jenis ini titik penghubung antar proses isotermal dan prose adiabatik juga mudah terlihat, sedangkan pada diagram realistik proses isotermal terlihat menerus ke proses adiabaik tanpa adanya titik penghubung.
Dua jenis diagram siklus Carnot akan dibuat, yang masing-masing mewakili jenis ilustratif dan jenis realistik.
Sebuah contoh ilustratif siklus Carnot disajikan berikut ini.
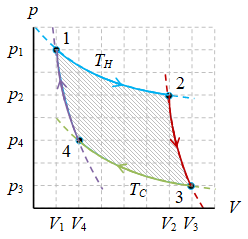
Gambar 2. Diagram siklus Carnot ilustratif dengan proses-proses: ekspansi isotermal ($1 \rightarrow 2$), ekspansi adiabatik ($2 \rightarrow 3$), kompresi isotermal ($3 \rightarrow 4$), dan kompresi adiabatik ($4 \rightarrow 1$).
Suatu siklus Carnot dibentuk oleh empat proses, yaitu proses ekspansi isotermal, ekspansi adiabatik, kompresi isotermal, dan kompresi adiabatik, dengan keempat proses tersebut telah disajikan pada Gambar 2. Terlihat pada contoh ini bahwa sumbu $p$ dan $V$ ujung kiri bawahnya bukan merupakan titik $(0, 0)$ sehingga proses-proses tersebut akan memotong kedua sumbu. Bila origin dari sumbu koordinat adalah $(0, 0)$ perpanjangan garis dari keempat proses tersebut tidak akan memotong kedua sumbu karena untuk proses isotermal $p \sim V^{-1}$ dan untuk proses adiabatik $p \sim V^{-\gamma}$.
Dengan menggunakan piranti lunak spreadsheet dapat dihasilkan digram siklus Carnot berikut ini.
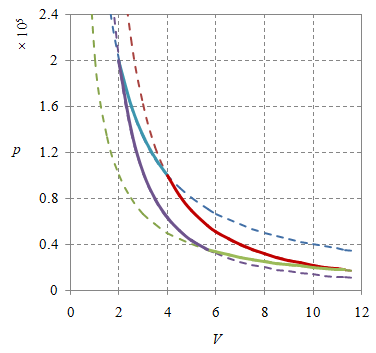
Gambar 3. Diagram siklus Carnot realistik dengan origin sumbu koordinat adalah $(0, 0)$.
Dapat dilihat dari Gambar 3 bahwa pilihan ini belum membuat diagram realistik menjadi lebih jelas, terutama agar dapat terbedakan proses isotermal dan proses adiabatik.
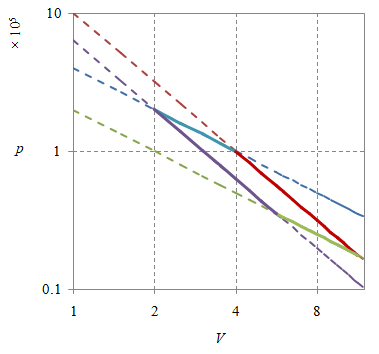
Gambar 4. Diagram siklus Carnot realistik dengan origin sumbu koordinat adalah $(0, 0)$ dan skala logaritmik pada kedua sumbu.
Alternatif lain adalah dengan menggunakan sumbu dengan skala logritmik seperti ditampilkan oleh Gambar 2, yang sayangnya belum juga memberikan ilustrasi yang lebih jelas. Gambar 3 dan 4 dibuat dengan $n = 24.05581$, $p_1 = 2\times 10^5$, $T_1 = 2000$, $V_1 = 2$, $p_2 = 10^5$, $T_2 = 2000$, $V_2 = 4$, $p_3 = 1.77\times 10^4$, $T_3 = 1000$, $V_3 = 11.3135$, $p_4 = 3.54\times 10^4$, $T_4 = 1000$, $V_4 = 5.65675$, dan $\gamma = 5/3$.
 |
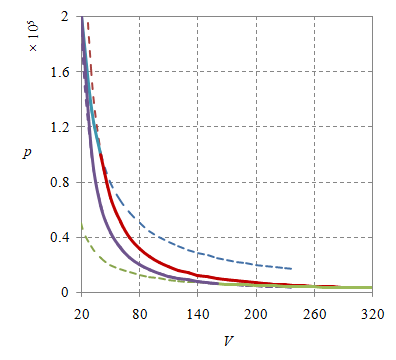 |
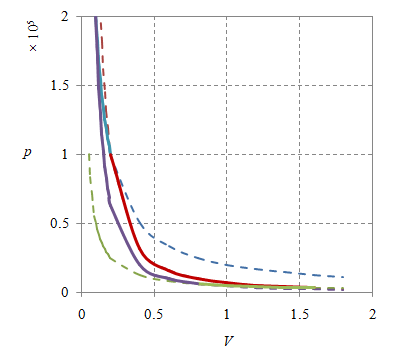
Gambar 5. Diagram siklus Carnot realistik dengan origin sumbu koordinat adalah $(0, 0)$ dan rentang tekanan-volume berbeda.
Pengubahan rentang tekanan dan volume juga belum memberikan gambar yang lebih jelas seperti pada Gambar 5, yang bagian kiri dibuat dengan dibuat dengan $n = 1.20279$, $p_1 = 2\times 10^5$, $T_1 = 2000$, $V_1 = 0.1$, $p_2 = 10^5$, $T_2 = 2000$, $V_2 = 0.2$, $p_3 = 3.13\times 10^3$, $T_3 = 500$, $V_3 = 1.6$, $p_4 = 6.25\times 10^3$, $T_4 = 500$, $V_4 = 0.8$, dan $\gamma = 5/3$, serta bagian kanan dengan $n = 120.279$, $p_1 = 2\times 10^5$, $T_1 = 4000$, $V_1 = 20$, $p_2 = 10^5$, $T_2 = 4000$, $V_2 = 40$, $p_3 = 3.13\times 10^3$, $T_3 = 1000$, $V_3 = 320$, $p_4 = 6.25\times 10^3$, $T_4 = 1000$, $V_4 = 160$, dan $\gamma = 5/3$.
 |
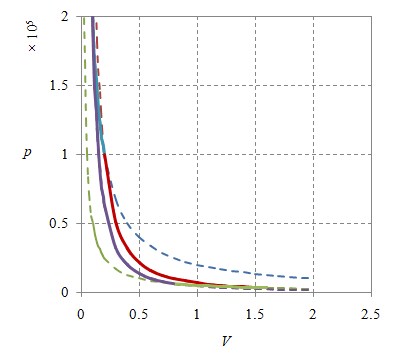 |
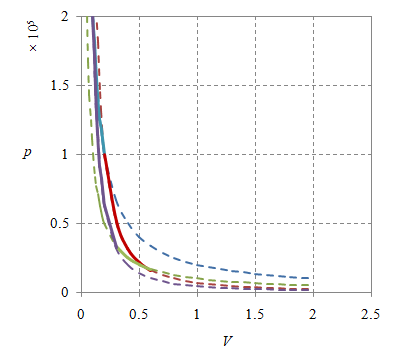
Gambar 6. Diagram siklus Carnot realistik dengan origin sumbu koordinat adalah $(0, 0)$ dan perbedaan titik ketiga.
Perubahan titik $3$ belum juga memberikan ilustrasi yang lebih jelas, seperti ditunjukkan oleh Gambar 6. Nomor-nomor keadaan telah diberikan pada Gambar 1. Gambar 6 bagian kiri dengan dibuat dengan $n = 1.20279$, $p_1 = 2\times 10^5$, $T_1 = 2000$, $V_1 = 0.1$, $p_2 = 10^5$, $T_2 = 2000$, $V_2 = 0.2$, $p_3 = 1.77\times 10^4$, $T_3 = 1000$, $V_3 = 0.56568$, $p_4 = 3.54\times 10^4$, $T_4 = 1000$, $V_4 = 0.28284$, dan $\gamma = 5/3$, serta bagian kanan dengan $n = 1.20279$, $p_1 = 2\times 10^5$, $T_1 = 2000$, $V_1 = 0.1$, $p_2 = 10^5$, $T_2 = 2000$, $V_2 = 0.2$, $p_3 = 3.13\times 10^3$, $T_3 = 500$, $V_3 = 1.6$, $p_4 = 6.25\times 10^3$, $T_4 = 500$, $V_4 = 0.8$, dan $\gamma = 5/3$.
Sedikit eksperimen dilakukan untuk menggunakan perumusan yang berbeda menggunakan $\gamma = 4$, tanpa arti fisis yang benar, dengan tujuan agar kemiringan kurva adiabatik amat jauh lebih curam dari sebelumnya ketimbang kurva isotermal.
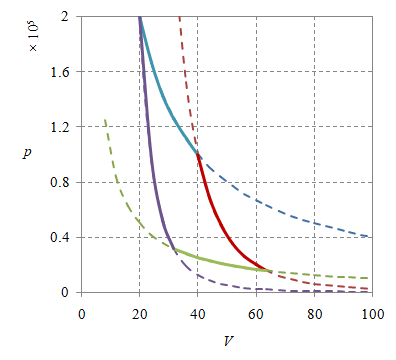
Gambar 7. Diagram siklus Carnot realistik dengan origin sumbu koordinat adalah $(0, 0)$ untuk $\gamma = 4$.
Dengan data-data berikut $n = 120.279$, $p_1 = 2\times 10^5$, $T_1 = 4000$, $V_1 = 20$, $p_2 = 10^5$, $T_2 = 4000$, $V_2 = 40$, $p_3 = 1.57\times 10^4$, $T_3 = 1000$, $V_3 = 63.496$, $p_4 = 3.15\times 10^4$, $T_4 = 1000$, $V_4 = 31.748$, dan $\gamma = 4$ Gambar 7 dapat dibuat. Selanjutnya, bila tidak disebutkan sebagai gas monoatomik, mungkin hal ini, demi agar diperoleh gambar yang lebih jelas, masih dapat diterima.
— Sparisoma Viridi (@6unpnp) December 9, 2021
ideal gas law • state, process, cycle • special processes