slr ls line

Garis atau kurva yang diperoleh untuk regresi linier sederhana dapat digambarkan dengan menggunakan kedua koefisien yang diperoleh dari metode least square, yang dikenal juga sebagai formula kemiringan kurva atau slope formula [1] atau dapat pula menggunakan lima parameter statistik [2]. Di sini hanya akan diilustrasikan kurva tersebut dan kurva lainnya yang kurang tepat.

simple linear regression

Bentuk persamaan

\begin{equation}\label{eqn:simple-linear-regression} y = a + bx + \varepsilon \end{equation}

dikenal sebagai formula regresi linier sederhana [3], dengan $\hat{y} = a + bx$ adalah nilai prediksi dari variabel terikat $y$ untuk setiap nilai dari variabel bebas $x$, $a$ adalah titik potong pada sumbu tegak, $b$ adalah koefisien regresi yang menggambarkan perkiraan seberapa besar $y$ berubah saat $x$ bertambah, $x$ adalah variabel bebas yang merupakan variabel yang diduga mempengaruhi $y$, dan $\varepsilon$ adalah kesalahan estimasi atau seberapa besar variasi dalam melakukan estimasi koefisien regresi.

sst, sse, r2

$\rm SST$ (sum of squares total) dan $\rm SSE$ (sum of squares error) adalah sebagai berikut [4]

\begin{equation}\label{eqn:sst} {\rm SST} = \sum_{i = 1}^n (y_i - \overline{y}_i)^2 \end{equation}

dan

\begin{equation}\label{eqn:sse} {\rm SSE} = \sum_{i = 1}^n (y_i - \hat{y}_i)^2 \end{equation}

dengan $n$ adalah jumlah pasangan data $\{(x_i, y_i), i = 1, \dots, n\}$. Dengan Persamaan \eqref{eqn:sse} dan \eqref{eqn:sst} dapat diperoleh coeffient of determination

\begin{equation}\label{eqn:r2} R^2 = 1 - \frac{ {\rm SSE} }{ {\rm SST} }, \end{equation}

di mana untuk pembilang, yang dalam hal ini adalah $\rm SSE$, kadang digunakan juga istilah $\rm SSR$ (sum squared regression) [5] atau $\rm SS_{res}$ (residual sum of squares) [6], yang merujuk ke hal yang sama. Akan tetapi kedua istilah tersebut berbeda dengan $\rm SSR$ (sum of squared regression) [4].

slope formula

Nilai $a$ dan $b$ pada Persamaan \eqref{eqn:simple-linear-regression} dapat diperoleh dengan formula kemiringan kurva [1]

\begin{equation}\label{eqn:slope-formula-a} a = \frac{ (\sum y)(\sum x^2) - (\sum x)(\sum xy) }{ n(\sum x^2) - (\sum x)^2 } \end{equation}

dan

\begin{equation}\label{eqn:slope-formula-b} b = \frac{ n(\sum xy) - (\sum x)(\sum y) }{ n(\sum x^2) - (\sum x)^2 }. \end{equation}

Setelah kedua nilai $a$ dan $b$ diperoleh garis dapat digambarkan pada data menggunakan persamaan

\begin{equation}\label{eqn:simple-linear-regression-line} y = a + bx, \end{equation}

tanpa suku kesalahan estimasi $\varepsilon$ bila dibandingkan dengan Persamaan \eqref{eqn:simple-linear-regression}.

curves

Dua buah kurva yang mengkuti Persamaan \eqref{eqn:simple-linear-regression-line} dengan nilai-nilai $a$ dan $b$ ditentukan secara intuitif diberikan pada gambar berikut ini.

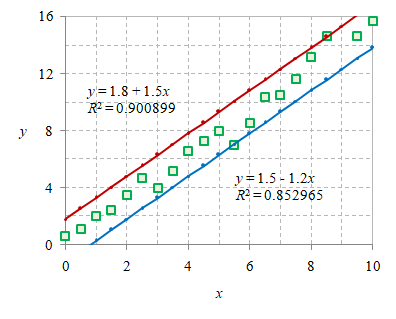
Gambar 1. Dua buah kurva yang mengapit data dari atas ($\color{#c00}{\mathbf{–}}$) dan bawah ($\color{#07c}{\mathbf{–}}$).

Garis berwarna merah ($\color{#c00}{\mathbf{–}}$) dengan persamaan $y = 1.8 + 1.5x$ merupakan perkiraan batas atas sebaran data dan garis berwarna biru ($\color{#07c}{\mathbf{–}}$) dengan persamaan $y = 1.5 - 1.2x$ merupakan perkiraan batas bawah sebaran data, dengan berturut-turut keduanya memberikan koefisien determinasi masing masing $0.900899$ dan $0.852965$.

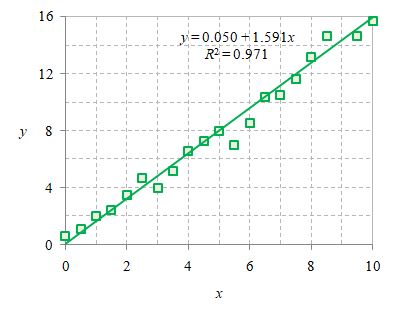
Gambar 2. Kurva hasil regresi linier dengan kuadrat terkecil atau nilai $a$ dan $b$ diperoleh menggunakan formula kemiringan kurva.

Dengan menggunakan Persamaan \eqref{eqn:slope-formula-a} dan \eqref{eqn:slope-formula-b} dapat diperoleh persamaan $y = 0.05 + 1.591x$ yang lebih baik dengan $R^2 = 0.971$ seperti diberikan pada Gambar 2.

data

Gambar 1 dan 2 dibuat dibuat dengan menggunakan data berikut yang semula dihasilkan dari persamaan $y = 0.5 + 1.5 x$

x	y	err	y(1+err)
0	0.5	0.2	0.6
0.5	1.25	-0.1	1.125
1	2	0	2.000
1.5	2.75	-0.1	2.475
2	3.5	0	3.500
2.5	4.25	0.1	4.675
3	5	-0.2	4.000
3.5	5.75	-0.1	5.175
4	6.5	0.01	6.565
4.5	7.25	0	7.250
5	8	0	8.000
5.5	8.75	-0.2	7.000
6	9.5	-0.1	8.550
6.5	10.25	0.01	10.353
7	11	-0.05	10.450
7.5	11.75	-0.01	11.633
8	12.5	0.05	13.125
8.5	13.25	0.1	14.575
9	14	0.2	16.800
9.5	14.75	-0.01	14.603
10	15.5	0.01	15.655

dan kemudian diberikan kesalahan err pada komponen vertikal dengan mengubahnya dari y menjadi y(1+err).

exer

1. Apakah kaitan antara Persamaan \eqref{eqn:simple-linear-regression} dan \eqref{eqn:sse}?
2. Apakah ada cara lain dalam menggambarkan garis selain pada Gambar 1?

note

1. Stephanie Glen, “Linear Regression: Simple Steps, Video. Find Equation, Coefficient, Slope” from StatisticsHowTo.com: Elementary Statistics for the rest of us!, 1 Jun 2018, url https://www.statisticshowto.com/probability-and-statistics/regression-analysis/find-a-linear-regression-equation/ [20211203].
2. Deborah J. Rumsey, “How to Calculate a Regression Line”, For Dummies, John Wiley & Sons, Inc., 26 Mar 2016, url https://www.dummies.com/education/math/statistics/how-to-calculate-a-regression-line/ [20211203].
3. Rebecca Bevans, “An introduction to simple linear regression”, Scribbr, 26 Oct 2020, url https://www.scribbr.com/statistics/simple-linear-regression/ [20211203].
4. Iliya Valchanov, “Sum of Squares Total, Sum of Squares Regression and Sum of Squares Error”, 365 Data Science, 5 Nov 2018, url https://365datascience.com/tutorials/statistics-tutorials/sum-squares/ [20211203].
5. “Coefficient of Determination, R-squared”, url https://www.ncl.ac.uk/webtemplate/ask-assets/external/maths-resources/statistics/regression-and-correlation/coefficient-of-determination-r-squared.html [20211203]
6. Wikipedia contributors, “Coefficient of determination”, Wikipedia, The Free Encyclopedia, 1 December 2021, 11:28 UTC, url https://en.wikipedia.org/w/index.php?oldid=1058089444 [20211203].

comments

#bug0211

— Sparisoma Viridi (@6unpnp) December 4, 2021

simple linear regression least square • slr ls gradient descent