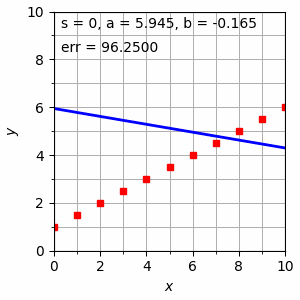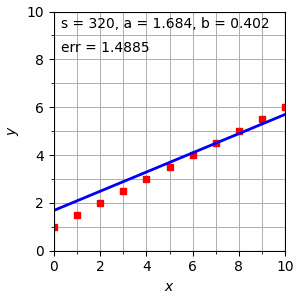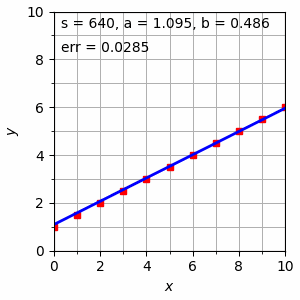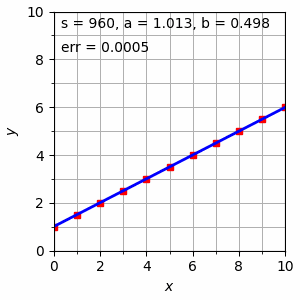
Gambar 1. Proses pencarian persamaan garis $y = a + bx$ melalui algoritma gradient descent.
Regresi merupakan salah satu permasalahan dalam machine learning (ML) dengan cara belajar supervised learning [1].
Untuk satu variabel bebas $x$ dan satu variabel terikat $y$ suatu prediktor dalam bentuk
\begin{equation}\label{eqn:0265-0} y = a + bx, \end{equation}
nilai $a$ dan $b$ dapat diperoleh menggunakan regresi linier.
Bila terdapat pasangan data $\{(x_i, y_i) \ | \ i = 1, 2, .., N \}$ nilai $a$ dan $b$ dapat diperoleh menggunakan least square yang menghasilkan
\begin{equation}\label{eqn:0265-1} a = \frac{\sum_{i = 1}^N y_i \sum_{i = 1}^N x_i^2 - \sum_{i = 1}^N x_i \sum_{i = 1}^N x_i y_i}{N \sum_{i = 1}^N x_i^2 - \left( \sum_{i = 1}^N x_i \right)^2} \end{equation}
dan
\begin{equation}\label{eqn:0265-2} b = \frac{N \sum_{i = 1}^N {x_i y_i} - \sum_{i = 1}^N x_i \sum_{i = 1}^N y_i}{N \sum_{i = 1}^N x_i^2 - \left( \sum_{i = 1}^N x_i \right)^2}. \end{equation}
Kesalahan antara data dan prediktor diberikan oleh
\begin{equation}\label{eqn:0265-3} \varepsilon = \sum_{i = 1}^N (a + b x_i - y_i)^2. \end{equation}
Persamaan \eqref{eqn:0265-1} dan \eqref{eqn:0265-2} diperoleh dengan menggunakan Persamaan \eqref{eqn:0265-3} melalui
\begin{equation}\label{eqn:0265-4} \frac{\partial \varepsilon}{\partial a} = 0, \ \ \ \ \frac{\partial \varepsilon}{\partial b} = 0. \end{equation}
Untuk ML nilai $a$ dan $b$ diubah dengan gradient descent melalui
\begin{equation}\label{eqn:0265-5} a^+ = a - \eta \frac{\partial \varepsilon}{\partial a} \end{equation}
dan
\begin{equation}\label{eqn:0265-6} b^+ = b - \eta \frac{\partial \varepsilon}{\partial b} \end{equation}
dengan $\eta$ adalah laju belajar. Indeks atas $+$ menunjukkan nilai baru dari kedua parameter, yang diubah agar kesalahan $\varepsilon$ berkurang. Idealnya akan tercapai nilai $a$ dan $b$ seperti pada Persamaan \eqref{eqn:0265-1} dan \eqref{eqn:0265-2}, yang tak lain adalah $a^+$ dan $b^+$ pada Persamaan \eqref{eqn:0265-5} dan \eqref{eqn:0265-6} saat Persamaan \eqref{eqn:0265-4} terpenuhi, yang ilustrasi pengubahan nilai-nilainya diberikan pada gambar berikut.

Gambar 1. Proses pencarian persamaan garis $y = a + bx$ melalui algoritma gradient descent.
Nilai err pada Gambar 1 di atas diberikan oleh Persamaan \eqref{eqn:0265-3}, yang telrihat semakin lama semakin kecil dengan berubahnya nilai-nilai $a$ dan $b$ melalui penerapan Persamaan \eqref{eqn:0265-5} dan \eqref{eqn:0265-6}. Gambar sebelumnya dapat diperoleh menggunakan kode Python berikut.
# Import required libraries
from numpy import sin, cos
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
xdata = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
ydata = np.array([1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6])
N = min(len(xdata), len(ydata))
a = 6
b = 0
eta = 0.001
def curve(a, b):
y = a + b * xdata
return y
# Create array for time t from tbed to tend with step dt
tbeg = 0
tend = 1000
dt = 1
t = np.arange(tbeg, tend, dt)
# Get range of x and y
#y = wave(0)
xmin = 0
xmax = 10
dx = 1
ymin = 0
ymax = 10
dy = 1
xmt = np.arange(xmin, xmax + dx, dx)
ymt = np.arange(ymin, ymax + dy, dy)
# Get figure for plotting and set it
fig = plt.figure(figsize=[3, 3])
# Configure axes
ax = fig.add_subplot()
ax.grid(which='both')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_xlim([xmin, xmax])
ax.set_ylim([ymin, ymax])
ax.set_xticks(xmt, minor=True)
ax.set_yticks(ymt, minor=True)
# It must be set after configuring axis to give the effect
fig.tight_layout(rect=[-0.03, -0.03, 1.03, 1.03])
# Prepare curve
mark, = ax.plot([], [], 'sr', lw=1, ms=4)
line, = ax.plot([], [], '-b', lw=2)
time_template = 's = %i, a = %.3f, b = %.3f'
time_text = ax.text(0.03, 0.93, '', transform=ax.transAxes)
err_template = 'err = %.4f'
err_text = ax.text(0.03, 0.83, '', transform=ax.transAxes)
# Perform animation
def init():
line.set_data([], [])
mark.set_data([], [])
time_text.set_text('')
err_text.set_text('')
return line, mark, time_text
def animate(i):
global a, b
eps = 0
depsda = 0
depsdb = 0
for j in range(0, N):
f = a + b * xdata[j]
eps += (f - ydata[j]) * (f - ydata[j])
depsda += 2 * (f - ydata[j]) * 1
depsdb += 2 * (f - ydata[j]) * xdata[j]
a = a - eta * depsda
b = b - eta * depsdb
s = i - 1
if s % 40 == 0:
y = curve(a, b)
line.set_data([xdata], [y])
mark.set_data([xdata], [ydata])
time_text.set_text(time_template % (s, a, b))
err_text.set_text(err_template % eps)
return line, mark, time_text
ani = animation.FuncAnimation(
fig, animate, np.arange(1, len(t)),
interval=5, blit=True, init_func=init
)
# Write to to a GIF animation
writergif = animation.PillowWriter(fps=40)
ani.save('0267.gif', writer=writergif)
— Sparisoma Viridi (@6unpnp) December 4, 2021
simple linear regression least square • slr ls line