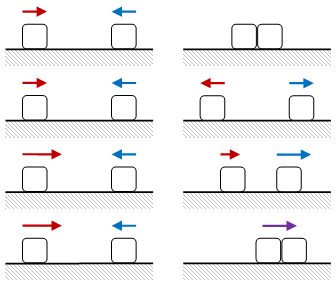
Gambar 1. Tumbukan dua benda yang saling mendekat sebagai keadaan awal dapat menghasilkan beberapa keadaan akhir seperti keduanya diam, keduanya berbalik arah, keduanya searah terpisah, dan keduanya searah sambil bergerak bersama-sama.
Momentum merupakan suatu besaran yang kekal, yang dalam suatu sistem tertutup total momentum bernilai tetap, di mana prinsip ini dikenal sebagai hukum kekekalan momentum atau kekalan momentum [1], yang merupakan bagian dari berbagai hukum-hukum kekekalan dalam fisika [2]. Perlu disadari bahwa momentum kekal dalam tumbukan, ledakan, dan peristiwa lain yang melibatkan banyak benda, di mana kekal berarti besaran itu, yang dalam hal ini adalah momentum selalu bernilai tetap selama suatu peristiwa berlangsung [3]. Kekekalan momentum juga digunakan dalam fluida, misalnya pada perumusan aliran tunak 1d [4]. Dalam pembelajaran hukum kekalan ini dapat diamati melalui eksperimen menggunakan linear air track dengan analisis citra gerak bendanya [5].
Hukum kekekalan momentum memiliki bentuk
\begin{equation}\label{eqn-momentum-conservation} \vec{p} _{1i} + \vec{p} _{2i} + \dots + \vec{p} _{Ni} = \vec{p} _{1f} + \vec{p} _{2f} + \dots + \vec{p} _{Nf}, \end{equation}
untuk sistem yang terdiri dari $N$ benda, dengan indeks $i$ berarti awal (inisial) dan $f$ berarti akhir (final). Atau dapat pula dituliskan dalam bentuk yang lebih kompak
\begin{equation}\label{eqn-momentum-conservation-compact} \sum_{j = 1}^{N} \vec{p}_j = \vec{p}_j’, \end{equation}
dengan notasi yang sedikit berbeda untuk keadaan awal tanpa indeks dan keadaan akhir tanpa indeks tetapi dengan tanda ‘. Digunakan notasi ini agar untuk keadaan awal tidak tertuliskan indeks $ji$ yang seperti seakan-akan dua indeks benda, padahal hanya satu indeks benda $j$ dan indeks $i$ menandakan keadaan awal. Untuk kasus 1d notasi vektor tidak harus digunakan.
Untuk peristiwa tumbukan 1d yang melibatkan dua benda terdapat beberapa kemungkinan keadaan akhir seperti terpisah bergerak pada arah berlawanan, terpisah tetapi bergerak pada arah yang sama, salah satu diam atau keduanya, bergerak bersama-sama, dan kemungkinan lainnya.

Gambar 1. Tumbukan dua benda yang saling mendekat sebagai keadaan awal dapat menghasilkan beberapa keadaan akhir seperti keduanya diam, keduanya berbalik arah, keduanya searah terpisah, dan keduanya searah sambil bergerak bersama-sama.
Salah satu keadaan awal tumbukan yang paling umum adalah dua benda bergerak saling mendekat. Beberapa keadaan awal dan keadaan akhir untuk tumbukan jenis ini diilustrasikan pada Gambar 1. Masih mungkin terdapat kemungkinan keadaan awal dan keadaan akhir yang lain.
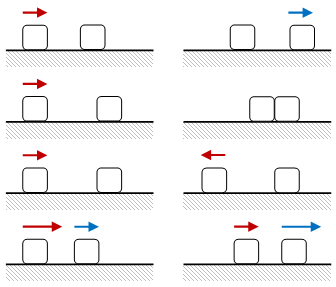
Gambar 2. Tumbukan dengan antara dua benda dengan keadaan awal benda kiri lebih besar lajunya dibandingkan benda di kanannya yang dapat pula nol, menghasilkan keadaan akhir berupa kedua benda bertukar kecepatan, keduanya diam, benda pertama berbalik arah sementara yang kedua tetap diam, dan benda pertama agak melambat sedangkan benda kedua bertambah cepat, di mana keduanya bergerak terpisah.
Selain saling mendekat terdapat pula keadaan awal di mana benda pertama mendekat benda kedua yang lebih lambat atau bahkan diam. Dengan kedaan awal ini terdapat beberapa keadaan akhir seperti diberikan pada Gambar 2 dan mungkin masih terdapat keadaan lain yang mungkin terjadi.
Kemungkinan-kemungkinan variasi keadaan awal dan akhir yang telah diberikan pada Gambar 1 dan 2 bergantung pada kecepatan masing-masing benda dan massanya. Untuk massa hal ini belum terlihat dengan jelas pada kedua gambar.
Ledakan sebenarnya merupakna kebalikan secara waktu dari Gambar 1 (atas). Pada ledakan keadaan awal kedua benda adalah bergerak atau diam bersama-sama, sedangkan keadaan akhirnya adalah terpisah, dan umumnya bergerak pada arah yang berlawanan.
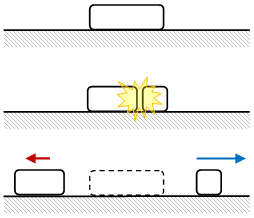
Gambar 3. Sebuah benda meledak dan menghasilkan dua buah bagian, bagian yang lebih besar bergerak ke arah kiri dan bagian lain yang lebih kecil bergerak ke arah kanan.
Sebuah benda yang semula diam meledak dan menghasilkan dua pecahan, pecahan yang besar akan bergerak lebih lambat dan pecahan yang lebih kecil akan bergerak lebih cepat. Kedua pecahan bergerak pada arah berlawanan. Ilustrasi mengenai hal ini diberikan pada Gambar 3.
Untuk tumbukan ataupun ledakan dalam 2d dan 3d yang melibatkan lebih dari dua benda, tetap menggunakan cara yang mirip dengan mematuhi Persamaan \eqref{eqn-momentum-conservation}. Bila masih tumbukan sepusat hanya dua benda akan tetapi kecepatannya dalam 2d atau 3d, secara prinsip tetap dapat dipilih suatu kerangka acuan sehingga tumbukan kedua benda kembali menjadi tumbukan 1d. Yang benar-benar 2d atau 3d adalah bila tumbukannya tidak sepusat.
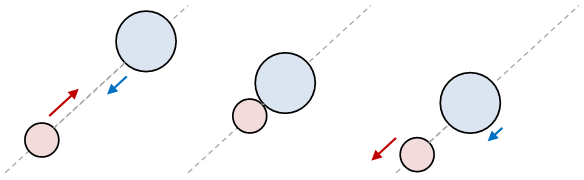
Gambar 4. Dua buah benda bertumbukan sepusat dengan kecepatan keduanya berupa vektor 2d.
Tumbukan dua benda dengan kecepatan masing-masing merupakan vektor 2d diberikan pada Gambar 4. Dengan memperhatikan garis putus-putus terlihat bahwa peristiwa tumbukan ini, karena masih merupakan tumbukan sepusat, sebenarnya adalah tumbukan 1d.
velocity • newton’s 1nd law • momentum