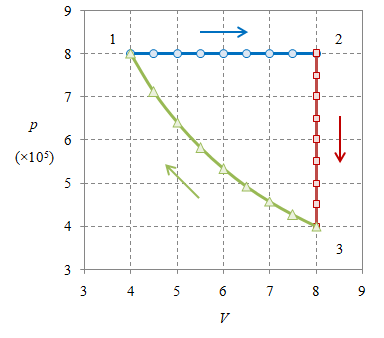
Gambar 1. Sejumlah $384.8695 \ \rm mol$ gas ideal monoatomik mengalami tiga proses $1 \rightarrow 2$, $2 \rightarrow 3$, dan $3 \rightarrow 1$.
Energi dalam atau energi internal suatu gas ideal merupakan fungsi dari temperatur saja [1], sehingga merupakan suatu variabel keadaan [2]. Energi dalam suatu gas adalah jumlah energi kinetik partikel-partikel dalam gas [3] dan juga energi potensialnya, yang untuk gas ideal diabaikan karena tidak ada interaksi inter-partikel [4]. Energi dalam dapat dituliskan dalam tiga besaran ekstensif, yaitu entropi, volume, dan massa [5].
Energi dalam suatu gas ideal monoatomik diberikan oleh [4]
\begin{equation}\label{eqn-internal-energy} U = \tfrac32 NkT = \tfrac32 nRT, \end{equation}
dengan $N$ jumlah partikel gas, $k$ konstanta Boltzmann, dan $T$ temperatur, serta $n$ jumlah mol gas. Dan perubahannya [1]
\begin{equation}\label{eqn-internal-energy-change} dU = C_V dT, \end{equation}
dengan $C_V = \frac32 nR$ adalah kapasitas panas pada volume tetap dan bila dilakukan integrasi akan diperoleh
\begin{equation}\label{eqn-internal-energy-change-integral} \Delta U = U_f - U_i = C_V (T_f - T_i) = C_V \Delta T, \end{equation}
dengan indeks $f$ dan $i$ masing-masing menggambarkan keadaan akhir (final) dan awal (inisial). Persamaan \eqref{eqn-internal-energy} menjelaskan bahwa untuk gas monoatomik energi dalam suatu gas terdiri dari energi translasi saja [6].
Energi dalam suatu gas merupakan suatu variabel keadaan sehingga perubahannya hanya bergantung pada keadaan awal dan keadaan akhir, tidak bergantung pada lintasan yang ditempuh suatu proses.

Gambar 1. Sejumlah $384.8695 \ \rm mol$ gas ideal monoatomik mengalami tiga proses $1 \rightarrow 2$, $2 \rightarrow 3$, dan $3 \rightarrow 1$.
Dengan menggunakan persamaan gas ideal dapat diperoleh bahwa $T_1 = 1000 \ \rm K$, $T_2 = 2000 \ \rm K$, dan $T_3 = 1000 \ \rm K$. Untuk gas monoatomik $C_V = \frac32 nR = 4799.99 \approx 4800 \ \rm J/K$. Dengan demikian dapat dihitung bahwa
\[\Delta U_{1 \rightarrow 2} = C_V (T_2 - T_1) = 4800 \cdot (2000-1000) = 4.8 \times 10^6 \ \rm J,\] \[\Delta U_{2 \rightarrow 3} = C_V (T_3 - T_2) = 4800 \cdot (1000-2000) = -4.8 \times 10^6 \ \rm J,\] \[\Delta U_{3 \rightarrow 1} = C_V (T_3 - T_2) = 4800 \cdot (1000-1000) = 0 \ \rm J,\]sehingga
\[\begin{array}{rcl} \Delta U_{1 \rightarrow 2 \rightarrow 3 \rightarrow 1} & = & \Delta U_{1 \rightarrow 2} + \Delta U_{2 \rightarrow 3} + \Delta U_{3 \rightarrow 1} \newline & = & 4.8 \times 10^6 - 4.8 \times 10^6 + 0 \newline & = & 0 \end{array}\]atau secara simbolik saja
\[\require{cancel} \newcommand\ccancel[2][black]{\color{#1}{\cancel{\color{black}{#2}}}} \newcommand\cbcancel[2][black]{\color{#1}{\bcancel{\color{black}{#2}}}} \newcommand\cxcancel[2][black]{\color{#1}{\xcancel{\color{black}{#2}}}} \begin{array}{rcl} \Delta U_{1 \rightarrow 2 \rightarrow 3 \rightarrow 1} & = & \Delta U_{1 \rightarrow 2} + \Delta U_{2 \rightarrow 3} + \Delta U_{3 \rightarrow 1} \newline & = & C_V (T_2 - T_1) + C_V (T_3 - T_2) + C_V (T_1 - T_3) \newline & = & \ccancel[red]{C_V T_2} - \cxcancel[green]{C_V T_1} + \cbcancel[blue]{C_V T_3} - \ccancel[red]{C_V T_2} + \cxcancel[green]{C_V T_1} - \cbcancel[blue]{C_V T_3} \newline & = & 0. \end{array}\]Perhitungan dengan simbolik pada baris kedua dari terakhir lebih disarankan ketimbang perhitungan numerik karena lebih dapat memperkenalkan kesalahan.
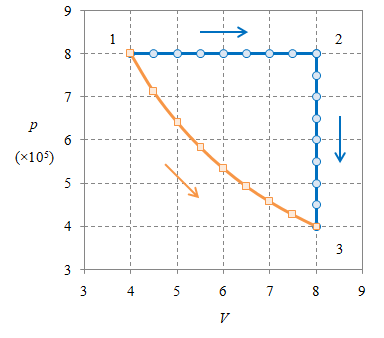
Gambar 2. Gas ideal monoatomik $384.8695 \ \rm mol$ mengalami dua proses terpisah, $1 \rightarrow 2 \rightarrow 3$ dan $1 \rightarrow 3$, yang memiliki keadaan awal dan akhir sama.
Ilustrasi pada Gambar 2, yang merupakan pengubahan dari Gambar 1, memberikan ilustrasi dua proses berbeda akan tetapi dengan keadaan awal dan akhir sama, yang akan memberikan
\[\Delta U_{1 \rightarrow 2 \rightarrow 3} = \Delta U_{1 \rightarrow 3}\]perubahan energi dalam gas yang sama.
kinetic theory of gases • ideal gas law • state, process, cycle • special processes