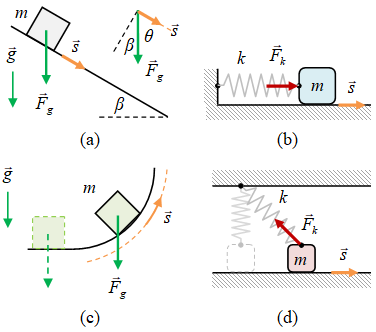
Gambar 1. Contoh sistem dengan variasi kemungkinan kontan atau tidaknya besar dan arah gaya yang bekerja pada benda terhadap arah lintasan untuk kategori: (a) $\rm I$, (b) $\rm II$, (c) $\rm III$, dan (d) $\rm IV$.
Kerja mengacu pada suatu aktivitas yang melibatkan gaya dan pergerakan dalam arah gaya tersebut [1] atau merupakan energi yang ditransfer ke atau dari obyek melalui penerapan gaya sepanjang suatu perpindahan [2], sehingga dapat dikatakan bahwa kerja mengukur transfer energi yang terjadi ketika suatu obyek berpindah menempuh suatu jarak disebabkan oleh gaya luar [3]. Terdapat tiga bahan utama dalam kerja yaitu gaya, perpindahan, dan penyebab, sehingga saat gaya disebut melakukan kerja pada suatu obyek harus terjadi perpindahan dan gaya tersebut yang menyebabkannya [4]. Dengan demikian hal ini dapat menjelaskan terdapatnya definisi bahwa dalam fisika, kerja didefinisikan sebagai suatu gaya yang menyebabkan pergerakan atau perpindahan suatu obyek [5], akan tetapi perlu diingat bahwa kerja bukan gaya. Secara teknis, kerja diperoleh melalui perkalian skalar antara gaya melalui aljabar dan perpindahan atau integral lintasan perpindahan dengan gaya melalui kalkulus [6]. Selanjutnya ukuran kemampuan dari sesuatu untuk melakukan kerja disebut sebagai energi [7]. Kata work dalam bahasa Inggris, yang diberi lambang $W$, diterjemahkan menjadi kerja atau usaha [8].
Suatu gaya $\vec{F}$ yang bekerja pada benda sehingga menyebabkan perpindahan sepanjang $\vec{s}$ akan menghasilkan kerja dalam bentuk
\begin{equation}\label{eqn:work-force-displacement-path-integral} W = \int \vec{F} \cdot d\vec{s}. \end{equation}
Rumusan ini berlaku umum untuk gaya konstan ataupun gaya yang berubah dengan $s$. Selain bentuk integral lintasan perpindahan-gaya pada Persamaan \eqref{eqn:work-force-displacement-path-integral}, kerja dapat pula dituliskan dalam bentuk [6]
\begin{equation}\label{eqn:work-force-displacement} W = \overline{F} \Delta s \cos\theta, \end{equation}
dengan $\theta$ adalah sudut antara gaya dan perpindahannya, dan $\overline{F}$ adalah gaya rata-rata yang bekerja pada benda. Proses perubahan dari Persamaan \eqref{eqn:work-force-displacement-path-integral} menjadi Persamaan \eqref{eqn:work-force-displacement} mirip seperti pada menghitung impuls, dengan integral gaya terhadap waktu atau dengan gaya rata-rata dikalikan selang waktu.
Usaha dapat memiliki tanda positif atau negatif. Keadaan pertama diperoleh bila selama perpindahan berlangsung proyeksi gaya pada lintasan atau produk skalar antara gaya dan lintasan lebih banyak bernilai positif dari yang bernilai negatif. Dan juga sebaliknya. Gaya gesek adalah satu penyebab usaha negatif bila gaya ini mengurangi kecepatan benda. Akan tetapi terdapat sistem di mana benda bergerak karena gaya gesek.
Terdapat empat kategori yang memiliki formulasi yang berbeda.
Bila arah dan besar gaya $\vec{F}_1$ yang bekerja pada suatu benda selalu tetap, kerja $W_1$ diberikan oleh
\begin{equation}\label{eqn:work-force-constant-magnitude-direction} W_1 = \vec{F}_1 \cdot \Delta\vec{s} = F_1 \Delta s \cos\theta \end{equation}
dengan $\vec{s}$ perpindahan benda yang disebabkan gaya tersebut dan $\theta$ sudut antara $\vec{F}_1$ dan $\vec{s}_1$.
Dapat pula gaya $\vec{F}_2$ hanya tetap arahnya akan tetapi tidak besarnya, dalam hal ini usaha $W_2$ diberikan oleh
\begin{equation}\label{eqn:work-force-constant-direction} W_2 = \int \vec{F}_2(s) \cdot d\vec{s} = \cos\theta \int F_2(s) ds, \end{equation}
dengan $d\vec{s}$ adalah elemen lintasan sepanjang arah perpindahan.
Selain kedua kasus di atas dapat pula terjadi bahwa besar gaya tetap, akan tetapi arahnya berubah-ubah sehingga
\begin{equation}\label{eqn:work-force-constant-magnitude} W_3 = \int \vec{F}_3(s) \cdot d\vec{s} = F_3 \int \cos\theta(s) ds, \end{equation}
dengan arah antara $\vec{F}_3$ dan $d\vec{s}$ merupakan fungsi dari $s$.
Untuk gaya dengan bentuk yang lebih umuma, yaitu yang arah dan besarnya berubah dengan berubahnya posisi benda sepanjang elemen perpindahan $d\vec{s}$
\begin{equation}\label{eqn:work-force-not-constant} W_4 = \int \vec{F}_4(s) \cdot d\vec{s} = \int F_4(s) \cos\theta(s) ds, \end{equation}
merupakan kerja yang dilakukan gaya $\vec{F}_4$. Perhatikan bahwa pada persamaan terakhir ini tidak ada suku baik dari besar gaya maupun arahnya yang dapat dikeluarga dari integral terhadap $ds$.
Kemungkinan kombinasi antara besar gaya dan arah gaya terhadap perpindahan yang telah disampaikan dapat disajikan dalam bentuk tabel berikut.
Tabel 1. Variasi sifat besar dan arah gaya dalam menghasilkan kerja ($0 \equiv$ konstan, $1 \equiv$ berubah).
| Kategori | $\dot{F}$ | $\dot{\theta}$ | Persamaan | Sistem |
|---|---|---|---|---|
| $\rm I$ | $0$ | $0$ | \eqref{eqn:work-force-constant-magnitude-direction} | Gaya gravitasi pada benda menuruni bidang miring licin |
| $\rm II$ | $1$ | $0$ | \eqref{eqn:work-force-constant-direction} | Gaya pegas horisontal pada benda di lantai mendatar licin |
| $\rm III$ | $0$ | $1$ | \eqref{eqn:work-force-constant-magnitude} | Gaya gravitasi pada benda menuruni lintasan melengkung licin |
| $\rm IV$ | $1$ | $1$ | \eqref{eqn:work-force-not-constant} | Gaya pegas vertikal pada benda di atas lantai mendatar licin |
Lambang titik di atas $F$ dan $\theta$ menandakan turunan terhadap waktu saat benda bergerak menempuh $s$. Bila bernilai nol artinya besaran tersebut kontan dan bila satu artinya berubah. Pemilikah karakter ini belum sepenuhnya tepat dan diharapkan tidak membingungkan. Ilustrasi keempat kategori sistem pada Tabel 1 diberikan pada Gambar 1 di bawah ini.

Gambar 1. Contoh sistem dengan variasi kemungkinan kontan atau tidaknya besar dan arah gaya yang bekerja pada benda terhadap arah lintasan untuk kategori: (a) $\rm I$, (b) $\rm II$, (c) $\rm III$, dan (d) $\rm IV$.
Selain keempat sistem yang diberikan pada Gambar 1, masih terdapat berbagai sistem yang dapat termasuk pada keempat kategori di atas. Seperti contoh suatu gaya konstan $F_1$ menarik benda di atas lantai mendatar licin dengan arah tertentu terhadap bidang mendatar tidak disajikan di sini, yang merupakan kategori $\rm I$, karena gaya konstan $F_1$ terkesan dipaksa untuk bernilai konstan, sedangkan pada contoh dengan menggunakan gaya gravitasi gaya berat di dekat permukaan bumi memang dapat dianggap konstan. Atau untuk kategori $\rm I$ digunakan gaya $F_2$ yang tidak konstan, di mana tidak konstannya agak dipaksakan. Untuk gaya pegas ketidakkonstanannya sudah merupakan sifat gaya pegas yang sebanding dengan regangan pegas.
Menurut hukum II Newton
\begin{equation}\label{eqn:newtons-2nd-law} \sum \vec{F} = m\vec{a}, \end{equation}
di mana suku $m\vec{a}$ merupakan gaya total. Menggunakan Persamaan \eqref{eqn:work-force-displacement-path-integral} atau \eqref{eqn:work-force-displacement} untuk gaya total ini akan dapat diperoleh usaha total pada benda. Dengan demikian sejauh semua gaya-gaya yang bekerja pada benda dapat dirumuskan, secara teori usaha pada atau oleh benda dapat dihitung. Kesulitan yang akan ditemui mungkin adalah penyelesaiannya secara matematika.
Terdapat sistem di mana kerja dapat didefinisikan, seperti sistem gas, listrik, dan magnet, di mana tidak hanya $F\Delta s$ akan tetapi juga dapat $p\Delta V$ dan $\tau d\theta$.
— Sparisoma Viridi (@6unpnp) December 7, 2021
newton’s 2nd law • displacement 2d • displacement 1d • vector 2d intro