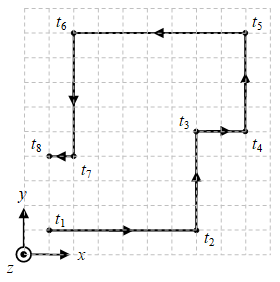
Gambar 1. Posisi benda pada $t = t_1, .., t_9$, dengan antar titik benda berpindah mengikuti lintasan berupa garis lurus dan satu kotak berukuran $1 \ {\rm m} \times 1 \ {\rm m}$.
Perpindahan merupakan suatu besaran vektor yang menyatakan seberapa jauh obyek dari posisi awalnya, atau dengan kata lain merupakan total perubahan posisi obyek [1], di mana perpindahan dihitung dengan mengurangi posisi akhir dengan posisi awal [2, 3, 4].
Perpindahan dihitung menggunakan
\begin{equation}\label{eqn-01} \Delta \vec{r} = \vec{r}_f - \vec{r}_i \end{equation}
dengan indeks $i$ dan $f$ berarti inisial (awal) dan final (akhir). Untuk kasus 1-D Persamaan \eqref{eqn-01} akan menjadi
\begin{equation}\label{eqn-02} \Delta x = x_f - x_i, \end{equation}
yang dapat bernilai positif ataupun negatif karena perpindahan merupakan besaran vektor.
Sebagai ilustrasi suatu benda bergerak dalam 2-d dengan informasi waktu $t$, posisi $(x, y)$ diberikan sebagai berikut ini, di mana dari satu titik ke titik lainnya benda bergerak dengan kecepatan konstan dan lintasan lurus.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $t_n \ (\rm s)$ | 0 | 2 | 6 | 8 | 12 | 14 | 16 | 20 |
| $x_n \ (\rm m)$ | 1 | 7 | 7 | 9 | 9 | 2 | 2 | 1 |
| $y_n \ (\rm m)$ | 1 | 1 | 5 | 5 | 9 | 9 | 4 | 4 |
Tabel sebelumnya dapat digambarkan seperti pada Gambar 1 berikut.

Gambar 1. Posisi benda pada $t = t_1, .., t_9$, dengan antar titik benda berpindah mengikuti lintasan berupa garis lurus dan satu kotak berukuran $1 \ {\rm m} \times 1 \ {\rm m}$.
Dengan demikian dapat dituliskan dengan menggunakan tabel atau Gambar 1, sebagai contoh, bahwa
\[\vec{r}_4 = 9 \hat{x} + 5 \hat{y},\]saat $t = t_4 = 8 \ \rm s$. Selanjutnya dapat diperoleh perpindahan antara $t = t_3$ dan $t = t_6$
\[\begin{array}{rcl} \Delta \vec{r}_{3-6} & = & \vec{r}_6 - \vec{r}_3 \newline & = & (2 \hat{x} + 9 \hat{y}) - (7 \hat{x} + 5 \hat{y}) \newline & = & (2 - 7) \hat{x} + (9 - 5) \hat{y} \newline & = & -5 \hat{x} + 4 \hat{y}, \end{array}\]dengan menggunakan Persaaman \eqref{eqn-01}. Perpindahan total antara $t = t_1$ sampai $t = t_8$ adalah
\[\begin{array}{rcl} \Delta \vec{r}_{1-8} & = & \vec{r}_8 - \vec{r}_1 \newline & = & (1 \hat{x} + 4 \hat{y}) - (1 \hat{x} + 1 \hat{y}) \newline & = & (1 - 1) \hat{x} + (4 - 1) \hat{y} \newline & = & 0 \hat{x} + 3 \hat{y} \newline & = & 3 \hat{y}. \end{array}\]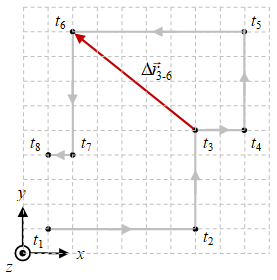
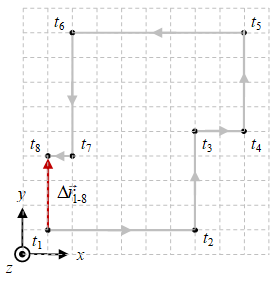
Gambar 2. Perpindahan $\Delta \vec{r}_{i-f}$ antara $t_i = t_3$ dan $t_f = t_6$ (kiri) dan antara $t_i = t_1$ dan $t_f = t_8$ (kanan).
Hasil perhitungan sebelumnya untuk $\vec{r} _{3-6}$ dan $\vec{r} _{1-8}$ dapat dikonfirmasi dengan menggunakan grafik seperti pada Gambar 2.
Selain ilustrasi dalam Gambar 2 terdapat pula cara lain untuk menggambarkan gerak benda, yaitu dalam bentuk grafik $x-t$ dan $y-t$ seperti pada Gambar 3 berikut.
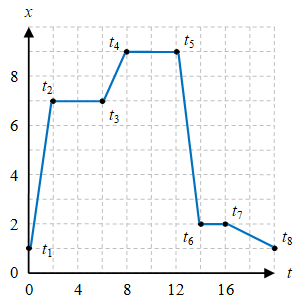
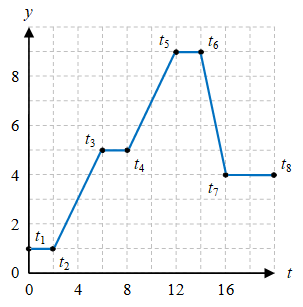
Gambar 3. Kurva $x-t$ (kiri) dan $y-t$ (kanan) untuk gerak benda mulai dari $t = t_1$ sampai $t = t_8$.
Perhatikan bahwa saat kurva merupakan garis mendatar, misalnya untuk $t_2 \le t \le t_3$ pada $x-t$, benda tidak bergerak pada arah tersebut (arah $x$).
meter • length • position • relative position • displacement 1d • distance 2d • distance 1d