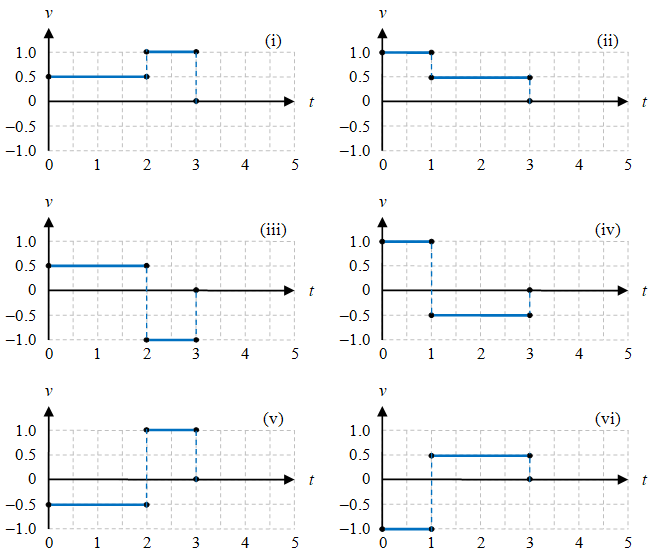
Gambar 1. Beberapa gerak lurus dengan dua kecepatan berbeda, dengan grid $0.5 \ {\rm s} \times 0.5 \ {\rm m/s}$.
Jarak yang merupakan besaran skalar merujuk pada seberapa banyak bumi yang dilingkupi oleh suatu obyek selama pergerakannya [1]. Persoalan menjadi lebih kompleks apabila benda bergerak dengan gerak konsekutif (berkelanjutan) [2], yang dapat dengan kecepatan berbeda (kadang dengan percepatan berbeda) pada setiap rentang waktunya.
Sebagai ilustrasi diambil kasus gerak lurus dalam 1-d, suatu gerak konsekutif dengan dua kecepatan berbeda, yang fungsi kecepatannya dapat dituliskan sebagai
\begin{equation}\label{eqn-1} v(t) = \left\{ \begin{array}{cc} v_1, & 0 \le t < t_1, \newline v_2, & t_1 \le t < t_2, \end{array} \right. \end{equation}
dengan beberapa variasi kasusnya adalah seperti diberikan dalam Gambar 1 berikut.

Gambar 1. Beberapa gerak lurus dengan dua kecepatan berbeda, dengan grid $0.5 \ {\rm s} \times 0.5 \ {\rm m/s}$.
Gambar 1 (i), (ii), (iii), (iv), (v), dan (vi) akan menghasilkan grafik $x-t$ yang berbeda sehingga akan pula memberikan besaran-besaran terkait $x$ yang berbeda.
Dengan hubungan
\begin{equation}\label{eqn-2} x_f - x_i = \int_{t_i}^{t_f} v \ dt \end{equation}
akan dapat diperoleh grafik $x-t$ dari grafik $v-t$ pada Gambar 1, yang dalam hal ini semua kecepatan bernilai tetap sehingga Persamaan \eqref{eqn-2} dapat disederhanakan menjadi
\begin{equation}\label{eqn-3} x_f = x_i + v (t_f - t_i). \end{equation}
Dalam menyelesaikan Persamaan \eqref{eqn-1} akan digunakan Persamaan \eqref{eqn-3} sebanyak dua kali, yaitu
\begin{equation}\label{eqn-4} x_1 = x(0) + v_1 (t_1 - 0) \end{equation}
dan
\begin{equation}\label{eqn-5} x_2 = x_1 + v_2 (t_2 - t_1), \end{equation}
dengan $x(0)$ merupakan syarat awal yang perlu diberikan. Perhatikan bahwa $x_1$ pada Persamaan \eqref{eqn-5} merupakan syarat awal akan tetapi nilanya diberikan oleh Persamaan \eqref{eqn-4}. Kaitan kedua Persamaan \eqref{eqn-4} dan \eqref{eqn-5} melalui $x_1$ telah menggambarkan sifat gerak konsekutif, selain bahwa $x(t)$ perlu selalu kontinu agar dapat memiliki turunan atau terdapat $v(t)$.
Selanjutnya, hanya untuk memudahkan, semua grafik $x-t$ pada Gambar 2 akan menggunakan syarat awal $x(0) = 0$.
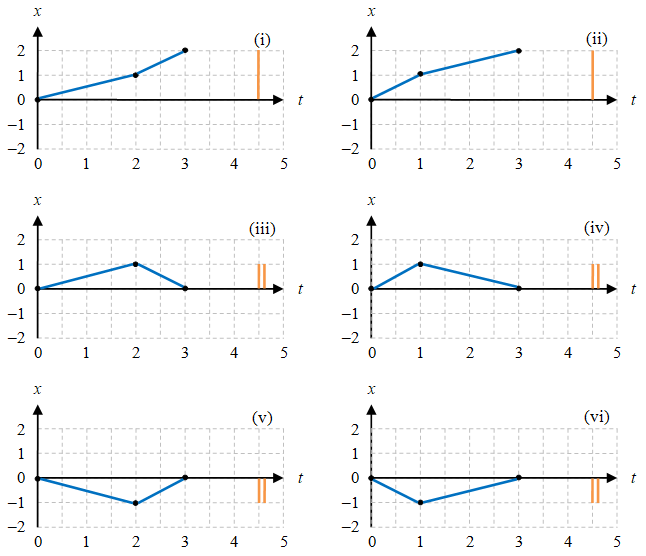
Gambar 2. Posisi benda untuk gerak konsekutif dengan dua kecepatan berbeda, dengan grid $0.5 \ {\rm s} \times 1 \ {\rm m}$.
Garis tegak oranye pada setiap grafik dalam Gambar 2 menunjukkan jarak yang ditempuh benda selama $3 \ \rm s$, yang memperlihatkan bahwa $2 \ \rm m$ merupakan jarak yang ditempuh untuk semua contoh gerak konsekutif yang diberikan.
Selain dengan menggunakan cara seperti pada Gambar 2 jarak yang ditempuh benda dapat pula diperoleh dengan menggunakan grafik $v-t$ dari Gambar 1, yaitu melalui menghitung luas di bawah kurva akan tetapi dengan nilai luas telah dimutlakkan. Nilai-nilai luas di bawah kurva yang belum dimutlakkan diberikan pada Gambar 3 berikut.
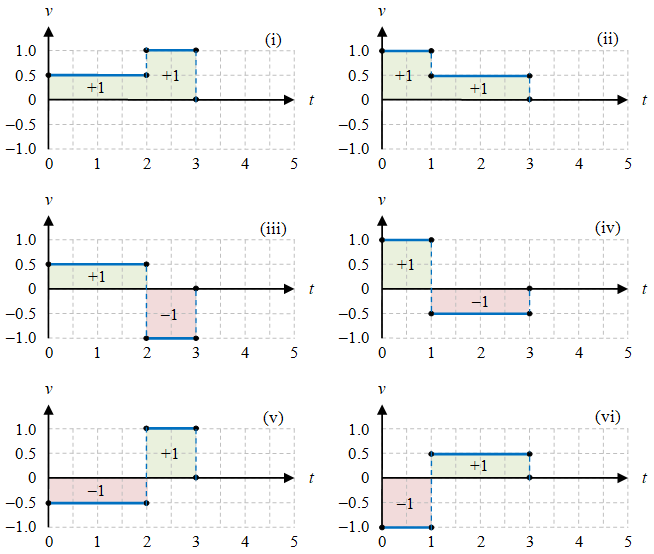
Gambar 3. Kecepatan benda untuk gerak konsekutif dengan dua kecepatan dan jarak total yang ditempuhnya, dengan grid $0.5 \ {\rm s} \times 0.5 \ {\rm m/s}$.
Dengan memutlakkan nilai-nilai luas di bawah kurva akan diperoleh jarak untuk masing-masing gerak pada Gambar 3 adalah seperti di bawah ini.
| Gambar 3 | Jarak | Perpindahan |
|---|---|---|
| (i) | $1 + 1 = 2 $ | $1 + 1 = 2$ |
| (ii) | $1 + 1 = 2 $ | $1 + 1 = 2$ |
| (iii) | $1 + |-1| = 2$ | $1 - 1 - 0$ |
| (iv) | $1 + |-1| = 2$ | $1 - 1 - 0$ |
| (v) | $|-1| + 1 = 2$ | $-1 + 1 - 0$ |
| (v) | $|-1| + 1 = 2$ | $-1 + 1 - 0$ |
Kolom ketiga pada tabel di atas bukan merupakan bahasan jarak akan tetapi ditambahkan hanya untuk menjadi pengingat perbedaan cara dalam menghitung jarak (kolom kedua) dan perpindahan (kolom ketiga).
Dari Gambar 1 dan 2 dapat diperoleh fungsi-fungsi berikut yang diajikan secara acak.
Suatu sel pada tabel di atas dapat dirujuk dengan baris dan kolomnya, misalnya untuk sel kanan atas adalah R1C3.
meter • length • position • relative position • displacement 2d • displacement 1d • distance 2d