relative position

Posisi relative adalah posisi suatu obyek dinyatakan secara relatif terhadap obyek lainnya [1], misalnya seseorang sedang naik kapal yang menyusuri suatu kanal. Posisi kapal umumnya dinyatakan terhadap bumi (tepi kanal, tanah) dan posisi orang dapat pula dinyatakan terhadap referensi yang sama (tepi kanal, tanah) atau dapat menggunakan posisi relatif terhadap kapal.

notation

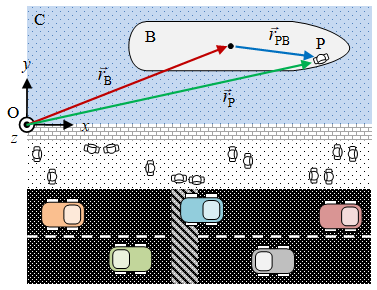
Sebagai ilustrasi akan dibahas kembali contoh pada bagian awal, yaitu penumpang $\rm P$ yang sedang menaiki kapal $\rm B$ yang sedang menyusuri kanal $\rm C$ dengan origin untuk kerangka acuan $\rm O$ diambil pada tepi kanal sebagaimana tersaji dalam Gambar 1 berikut.

Gambar 1. Penumpang $\rm P$ yang berada di atas kapal $\rm B$ yang sedang menyusuri kanal $\rm C$.

Posisi kapal ${\rm B}$ terhadap origin (tepi kanal) diberikan oleh $\vec{r}_{\rm B}$ dan posisi penumpang ${\rm P}$ terhadap origin diberikan oleh $\vec{r} _{\rm P}$. Posisi relatif penumpang $\rm P$ terhadap kapal $\rm B$ diberikan oleh

\begin{equation}\label{eqn-01} \vec{r} _{\rm PB} = \vec{r} _{\rm P} - \vec{r} _{\rm B}. \end{equation}

Mungkin untuk memudahkan mengingatnya, dapat dituliskan

\begin{equation}\label{eqn-02} \vec{r} _{\rm PO} = \vec{r} _{\rm P} - \vec{r} _{\rm O}. \end{equation}

dan

\begin{equation}\label{eqn-03} \vec{r} _{\rm BO} = \vec{r} _{\rm B} - \vec{r} _{\rm O}, \end{equation}

bahwa saat suatu posisi dinyatakan terhadap suatu orgin, $\vec{r}_{\rm O} = (0, 0, 0)$, sebenarnya posisi tersebut telah dikurangi terhadap posisi origin yang dimaksud ${\rm O}(0, 0, 0)$.

numerical calculation

Perhitungan secara numerik dalam menyelesaikan permasalahan fisika dianjurkan karena kesulitan yang dihadapi peserta ajar akan menjadi pengalaman berharga untuk meningkatkan pemahaman dan kemampuan mereka [2]. Untuk itu contoh Gambar 1 sebelumnya akan ditingkatkan kesulitannya menjadi seperti dalam Gambar 2 berikut.

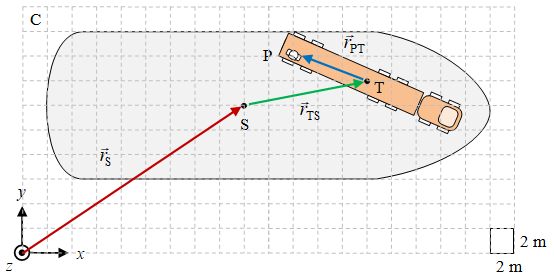
Gambar 2. Penumpang $\rm P$ yang berada di atas truk $\rm T$ yang berada di atas kapal $\rm S$ yang sedang menyusuri kanal $\rm C$ dengan ukuran grid $2 \ {\rm m} \times 2 \ {\rm m}$.

Dari Gambar 2 dapat diperoleh bahwa

Selain Persamaan \eqref{eqn-01} dapat pula dituliskan hubungan dalam bentuk

\begin{equation}\label{eqn-04} \vec{r} _{\rm P} = \vec{r} _{\rm PT} + \vec{r} _{\rm TS} + \vec{r} _{\rm S}, \end{equation}

sehingga dengan menggunakan ketiga persamaan sebelumnya dapat diperoleh bahwa

yang hasilnya dapat dikonfirmasi dengan menghitung grid untuk $\vec{r} _{\rm P}$ dalam Gambar 2.

exer

1. Dengan menggunakan informasi dari Gambar 2 tentukanlah $\vec{r} _{\rm T}$ secara langsung dengan menghitung grid dan dengan menggunakan informasi $\vec{r} _{\rm S}$ dan $\vec{r} _{\rm TS}$. Kemudian bandingkan hasil keduanya dan apakah sama hasilnya?
2. Bila kapal $\rm S$ bergerak maju searah $x+$ dengan besar kecepatan $v_{\rm Sx} = 4 \ \rm m/s$. Tuliskan rumusan posisi setiap saat kapal $\rm S$ bila saa $t = 0 \ \rm s$ posisinya adalah seperti pada Gambar 2.

note

1. -, “Relative Velocities and Relative Positions”, IGCE Math Notes, url https://astarmathsandphysics.com/igcse-maths-notes/510-relative-velocities-and-relative-positions.html [20211004].
2. Rhett Allain, “You Physics Teachers Really Ought to Teach Numerical Calculations”, Wired, 4 Mar 2017, url https://www.wired.com/2017/03/physics-teachers-really-teach-numerical-calculations/ [20211004].

vector 2d intro • meter • length • position • displacement 2d • displacement 1d • distance 2d • distance 1d