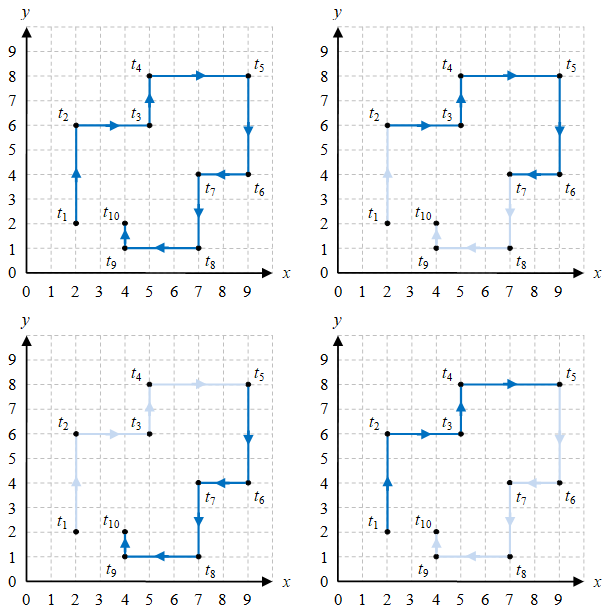
Gambar 1. Benda bergerak mulai dari waktu $t_1$ sampai $t_{10}$, di mana gerak antar titik mengikuti lintasan berupa garis lulus, dengan grid $1 \ {\rm m} \times 1 \ {\rm m}$.
Jarak merupakan besaran skalar yang merujuk pada seberapa banyak (seberapa panjang) tanah (lintasan) yang dilingkupi (dijelajahi) selama suatu obyek bergerak [1], atau mungkin lebih tepatnya dapat disebut sebagai panjang lintasan.
Suatu benda bergerak dari satu titik ke titik lain mengikuti lintasan garis lulus seperti diberikan oleh Gambar 1 berikut.

Gambar 1. Benda bergerak mulai dari waktu $t_1$ sampai $t_{10}$, di mana gerak antar titik mengikuti lintasan berupa garis lulus, dengan grid $1 \ {\rm m} \times 1 \ {\rm m}$.
Pada kiri atas Gambar 1 tergambarkan keseluruhan lintasan yang ditempuh benda mulai dari waktu $t = t_1$ sampai $t = t_{10}$ yang akan memberikan jarak (atau panjang lintasan) $26 \ \rm m$. Selanjutnya, bagian kanan atas adalah jarak yang ditempuh benda mulai dari waktu $t = t_2$ sampai $t = t_7$ dengan nilai $15 \ \rm m$, bagian kiri bawah adalah jarak yang ditempuh benda mulai dari waktu $t = t_5$ sampai $t = t_{10}$ dengan nilai $13 \ \rm m$, dan bagian kanan bawah adalah jarak yang ditempuh benda mulai dari waktu $t = t_1$ sampai $t = t_5$ dengan nilai $13 \ \rm m$.
Selain Gambar 1 dapat pula dibuat banyak variasi gerak 2-d untuk mengilustrasikan bagaimana menghitung jarak. Beberapa contohnya adalah seperti diberikan oleh Gambar 2 berikut ini. Keterangan NW (north west) adalah kiri atas, NE (north east) kanan atas, SW (south west) kiri bawah, dan SE (south east) kanan bawah.
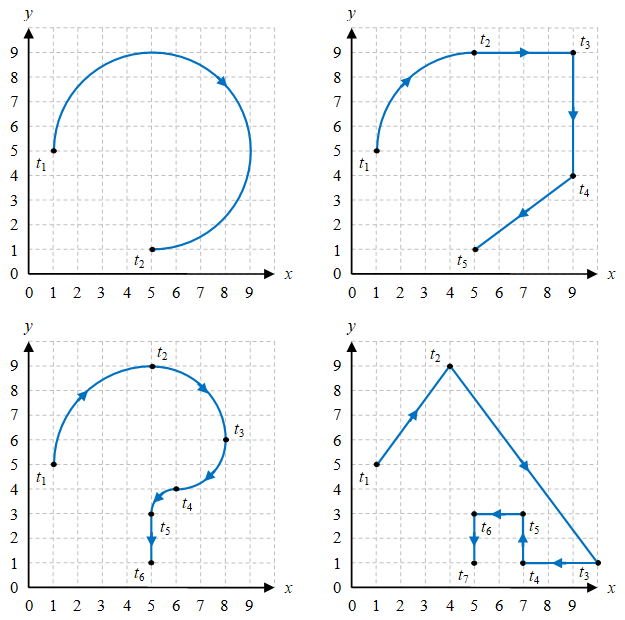
Gambar 2. Dengan grid $1 \ {\rm m} \times 1 \ {\rm m}$, digambarkan berbagai lintasan benda yang bergerak dari waktu awal (inisial) $t_i$ sampai waktu akhir (final) $t_f$ dengan berbagai bentuk gerak: gerak melingkar (NW), gerak melingkar dan rangkaian gerak lurus (NE), rangkaian gerak melingkar dan gerak lurus (SW), dan rangkaian gerak lurus (SE).
Dapat diperoleh dari Gambar 2 bahwa
\[L_{\rm NW} = \frac34 \cdot 2\pi \cdot R = 6 \pi \ {\rm m},\] \[\begin{array}{rcl} L_{\rm NE} & = & \frac14 \cdot 2\pi \cdot R + L_{23} + L_{34} + L_{45} \newline & = & 2\pi + 4 + 5 + 5 = (2\pi + 14) \ {\rm m}, \end{array}\] \[\begin{array}{rcl} L_{\rm SE} & = & L_{12} + L_{23} + L_{34} + L_{45} + L_{56} + L_{67} \newline & = & 5 + 10 + 3 + 2 + 2 + 2 = 24 \ {\rm m}, \end{array}\]sedangkan untuk $L_{\rm SW}$ silakan dihitung sebagai latihan.
meter • length • position • relative position • displacement 2d • displacement 1d • distance 1d