
Gambar 1. Beberapa muatan dan garis-garis yang menggambarkan jarak antar dua muatan, serta gaya tarik-menarik ($\color{#0b5}{\blacksquare}$) dan gaya tolak-menolak ($\color{#fc0}{\blacksquare}$) antar dua muatan.
Gaya antar dua benda bermuatan disebut sebagai listrik [1, 2, 3], gaya elektrik [4, 5], gaya elektrostatik [6, 7], atau gaya Coulomb [8]. Gaya elektrostatik termasuk di dalam gaya elektromagnetik [9], dengan gaya elektromagnetik bersama-sama dengan gaya gravitasi, gaya nuklir kuat, dan gaya nuklir lemah merupakan empat gaya fundamental yang membentuk kompleksitas alam semesta di sekitar kita [10].
Besar gaya elektrostatik antara dua buah muatan $q_i$ dan $q_j$ yang terpisah jarak $r_{ij}$ diberikan oleh
\begin{equation}\label{eqn-electrostatic-force-two-point-charges} F_{ij} = F_{ji} = k \frac{ |q_i| |q_j|}{r_{ij}^2} \end{equation}
yang dikenal sebagai hukum Coulomb untuk gaya listrik [3], dengan $k$ adalah konstanta elektrostatik yang dalam tiga angka berarti adalah $8.99 \times 10^9 \ {\rm N \cdot m^2/C^2}$ [11] atau juga disebut konstanta Coulomb yang bila dengan lebih banyak angka berarti menjadi $8.987551787$ $\times$ $10^9$ ${\rm N \cdot m^2/C^2}$ dengan saat kuliah di universitas sering diajari cara mudah untuk mengingat nilai ini sebagai $9 \times 10^9$ [12].

Gambar 1. Beberapa muatan dan garis-garis yang menggambarkan jarak antar dua muatan, serta gaya tarik-menarik ($\color{#0b5}{\blacksquare}$) dan gaya tolak-menolak ($\color{#fc0}{\blacksquare}$) antar dua muatan.
Persamaan \eqref{eqn-electrostatic-force-two-point-charges} hanya memberikan besar gaya dan belum arahnya, sehingga bila terdapat tiga muatan seperti pada Gambar 1 gaya dapat berlaku sebagai gaya tarik-menarik atau gaya tolak-menolak, terlebih bila tanda muatan belum didefinisikan.
Sebagai contoh diberikan gambar enam titik muatan untuk dihitung gaya antar dua muatannnya.

Gambar 2. Enam buah muatan $q_i = q = 12 \ {\rm \mu C}$, $i = 1, 2, \dots, 6,$ terpisahkan dengan jarak yang berkelipatan $1 \ {\rm \mu m}$.
Dengan menggunakan informasi dalam Gambar 2 dan rumusan dalam Persamaan \eqref{eqn-electrostatic-force-two-point-charges} dapat dihitung $F_{54}$, $F_{32}$, dan $F_{24}$, yaitu
\begin{equation}\label{eqn:fcoul-f54} \begin{array}{rcl} F_{45} & = & \displaystyle k \frac{|q_4| |q_5|}{r_{45}^2} = k \frac{|12\mu| |12\mu|}{(3\mu)^2} \newline & = & \displaystyle k \frac{144 \mu^2}{9 \mu^2} = 16k, \end{array} \end{equation}
\begin{equation}\label{eqn:fcoul-f32} \begin{array}{rcl} F_{32} & = & \displaystyle k \frac{|q_3| |q_2|}{r_{32}^2} = k \frac{|12\mu| |12\mu|}{(4\mu)^2} \newline & = & \displaystyle k \frac{144 \mu^2}{16 \mu^2} = 9k, \end{array} \end{equation}
\begin{equation}\label{eqn:fcoul-f24} \begin{array}{rcl} F_{24} & = & \displaystyle k \frac{|q_2| |q_4|}{r_{24}^2} = k \frac{|12\mu| |12\mu|}{(5\mu)^2} \newline & = & \displaystyle k \frac{144 \mu^2}{25 \mu^2} = 5.76k. \end{array} \end{equation}
Hasil pada Persamaan \eqref{eqn:fcoul-f54}, \eqref{eqn:fcoul-f32}, dan \eqref{eqn:fcoul-f24} masih dalam $k$, yang untuk mendapatkan nilai numerik akhirnya masih perlu disubstitusikan, misalnya untuk kemudahan dengan $k \approx 9 \times 10^9 \ {\rm N \cdot m^2/C^2}$, yang akan memberikan hasil $F_{45} = 144 \ {\rm GN}$, $F_{32} = 81 \ {\rm GN}$, dan $F_{24} = 51.84 \ {\rm GN}$. Perhatikan bahwa telah digunakan prefiks SI sehingga satuannya menjadi giganewton, di mana $1 \ {\rm GN} = 10^9 \ {\rm N}$.
Bila tanda muatan, positif ($+$) dan negatif($-$) diikutsertakan, rumusan pada Persamaan \eqref{eqn-electrostatic-force-two-point-charges} perlu diubah menjadi
\begin{equation}\label{eqn-electrostatic-force-two-point-charges-vector} \vec{F} _{ij} = k \frac{ q_i q_j}{r _{ij}^2} \ \hat{r} _{ij} \end{equation}
dengan
\begin{equation}\label{eqn-relative-position} \vec{r}_{ij} = \vec{r}_i - \vec{r}_j, \end{equation}
\begin{equation}\label{eqn-distance-two-points} r_{ij} = |\vec{r} _{ij}| = \sqrt{\vec{r} _{ij} \cdot \vec{r} _{ij}}, \end{equation}
\begin{equation}\label{eqn-unit-vector} \hat{r} _{ij} = \frac{\vec{r} _{ij}}{r _{ij}}. \end{equation}
Sebagai ilustrasi terdapat dua buah muatan yang tandanya belum diketahui dengan posisi masing-masing diberikan pada gambar berikut ini.

Gambar 3. Dua buah muatan $q_1$ dan $q_2$ yang masing-masing terletak pada $(3 \ {\rm\mu m}, 3 \ {\rm\mu m})$ dan $(6 \ {\rm\mu m}, 6 \ {\rm\mu m})$.
Ingin dihitung gaya $\vec{F} _{12}$ atau gaya pada muatan $q_1$ akibat keberadaan muatan $q_2$ dan gaya $\vec{F} _{21}$ atau gaya pada muatan $q_2$ akibat keberadaan muatan $q_1$.
Dari Gambar 3 dapat diperoleh informasi
\begin{equation}\label{eqn:info-r1} \vec{r}_1 = (3 \hat{x} + 3 \hat{y}) \times 10^{-6} \ {\rm m} \end{equation}
dan
\begin{equation}\label{eqn:info-r2} \vec{r}_2 = (6 \hat{x} + 6 \hat{y}) \times 10^{-6} \ {\rm m}. \end{equation}
Dengan Persamaan \eqref{eqn-relative-position}, \eqref{eqn-distance-two-points}, dan \eqref{eqn-unit-vector} serta Gambar 3 dapat dihitung vektor posisi relatif, jarak antar dua titik, dan vektor satuannya.
Penerapan Persamaan \eqref{eqn-relative-position} untuk muatan $q_1$ menghasilkan
\begin{equation}\label{eqn:r12} \begin{array}{rcl} \vec{r}_{12} & = & \vec{r}_1 - \vec{r}_2 \newline & = & [(3 \hat{x} + 3 \hat{y}) \times 10^{-6}] - [(6 \hat{x} + 6 \hat{y}) \times 10^{-6}] \newline & = & [(3 \hat{x} + 3 \hat{y}) - (6 \hat{x} + 6 \hat{y})] \times 10^{-6} \newline & = & [(3 - 6) \hat{x} + (3 - 6) \hat{y})] \times 10^{-6} \newline & = & (-3 \hat{x} -3 \hat{y}) \times 10^{-6} \newline & = & -3(\hat{x} + \hat{y}) \times 10^{-6} \end{array} \end{equation}
dan untuk muatan $q_2$
\begin{equation}\label{eqn:r21} \begin{array}{rcl} \vec{r}_{21} & = & \vec{r}_2 - \vec{r}_1 \newline & = & [(6 \hat{x} + 6 \hat{y}) \times 10^{-6}] - [(3 \hat{x} + 3 \hat{y}) \times 10^{-6}] \newline & = & [(6 \hat{x} + 6 \hat{y}) - (3 \hat{x} + 3 \hat{y})] \times 10^{-6} \newline & = & [(6 - 3) \hat{x} + (6 - 3) \hat{y})] \times 10^{-6} \newline & = & (3 \hat{x} 3 \hat{y}) \times 10^{-6} \newline & = & 3(\hat{x} + \hat{y}) \times 10^{-6}. \end{array} \end{equation}
Persamaan \eqref{eqn:r12} dan \eqref{eqn:r21} telah memberikan konfirmasi hubungan
\begin{equation}\label{eqn:r21-r12} \vec{r} _{21} = - \vec{r} _{12} \end{equation}
secara numerik.
Penerapan Persamaan \eqref{eqn-distance-two-points} pada Persamaan \eqref{eqn:r12} dan \eqref{eqn:r12} akan menghasilkan
\begin{equation}\label{eqn:r12-distance} \begin{array}{rcl} r_{12} & = & | \vec{r}_{12} | = \sqrt{\vec{r} _{12} \cdot \vec{r} _{12}} \newline & = & 3 \sqrt{-(\hat{x} + \hat{y}) \cdot -(\hat{x} + \hat{y})} \times 10^{-6} \newline & = & 3 \sqrt{2} \times 10^{-6} \end{array} \end{equation}
dan
\begin{equation}\label{eqn:r21-distance} \begin{array}{rcl} r_{21} & = & | \vec{r}_{21} | = \sqrt{\vec{r} _{21} \cdot \vec{r} _{21}} \newline & = & 3 \sqrt{(\hat{x} + \hat{y}) \cdot (\hat{x} + \hat{y})} \times 10^{-6} \newline & = & 3 \sqrt{2} \times 10^{-6}, \end{array} \end{equation}
yang dapat diperoleh juga melalui Persaamaan \eqref{eqn:r21-r12} dengan
\begin{equation}\label{eqn:r21-r12-magnitude} \begin{array}{rcl} |\vec{r} _{21}| & = & |- \vec{r} _{12}| \newline r _{12} & = & r _{21}. \end{array} \end{equation}
Selanjutnya adalah menerapkan Persamaan \eqref{eqn-unit-vector} yang memberikan
\begin{equation}\label{eqn:r12-unit} \begin{array}{rcl} \hat{r} _{12} & = & \displaystyle \frac{\vec{r} _{12}}{r _{12}} \newline & = & \displaystyle \frac{-3(\hat{x} + \hat{y}) \times 10^{-6}}{3 \sqrt{2} \times 10^{-6}} \newline & = & \displaystyle -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \end{array} \end{equation}
dan
\begin{equation}\label{eqn:r21-unit} \begin{array}{rcl} \hat{r} _{21} & = & \displaystyle \frac{\vec{r} _{21}}{r _{21}} \newline & = & \displaystyle \frac{3(\hat{x} + \hat{y}) \times 10^{-6}}{3 \sqrt{2} \times 10^{-6}} \newline & = & \displaystyle \frac12 \sqrt{2} (\hat{x} + \hat{y}). \end{array} \end{equation}
Dengan demikian penyebut dan vektor satuan untuk Persamaan \eqref{eqn-electrostatic-force-two-point-charges-vector} telah diperoleh.
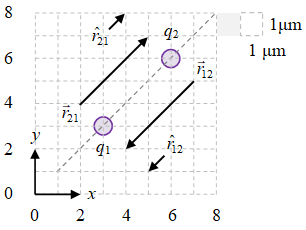
Gambar 4. Vektor-vektor posisi relatif dan vektor-vektor satuan untuk kedua muatan.
Ilustrasi vektor-vektor untuk Persamaan \eqref{eqn:r12} dan \eqref{eqn:r12-unit} diberikan pada Gambar 4 di bagian kanan bawah sedang untuk Persamaan \eqref{eqn:r21} dan \eqref{eqn:r21-unit} vektor-vektornya diberikan pada Gambar 4 di bagian kiri atas. Vektor-vektor mengarah pada muatan yang sedang ditinjau dan berasal dari muatan penyebabnya. Perhatikan bahwa untuk vektor satuan, besarnya adalah satu.
Bila $q_1 = +3 \ {\rm nC}$ dan $q_2 = +3 \ {\rm nC}$ dan vektor-vektor posisi relatif dan vektor-vektor satuan untuk kedua muatan diperoleh dari Persamaan \eqref{eqn:r12} dan \eqref{eqn:r12-unit} untuk $\vec{F} _{12}$ dan dari Persamaan \eqref{eqn:r21} dan \eqref{eqn:r21-unit} untuk $\vec{F} _{21}$, maka dapat diperoleh
\begin{equation}\label{eqn:f12-case-1} \begin{array}{rcl} \vec{F} _{12} & = & \displaystyle k \frac{q_1 q_2}{r _{12}^2} \hat{r} _{12} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+3 \ {\rm n})(+3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{-\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right] \end{array} \end{equation}
dan
\begin{equation}\label{eqn:f21-case-1} \begin{array}{rcl} \vec{F} _{21} & = & \displaystyle k \frac{q_2 q_1}{r _{21}^2} \hat{r} _{21} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+3 \ {\rm n})(+3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right]. \end{array} \end{equation}
Persamaan \eqref{eqn:f12-case-1} dan \eqref{eqn:f21-case-1} ditulikan dalam bentuk $\rm(\color{#f90}{besar})[\color{#0b5}{arah}]$ sehingga memudahkan untuk memilah informasi mengenai kedua gaya bila diperlukan.

Gambar 5. Dua buah muatan positif dan gaya yang bekerja pada masing-masing muatan akibat adanya muatan lain.
Arah kedua gaya pada Persamaan \eqref{eqn:f12-case-1} dan \eqref{eqn:f21-case-1} disajikan dalam Gambar 5, dengan gaya pertama yang bekerja muatan $q_1$ mengarah ke kiri bawah dan gaya kedua yang bekerja pada muatan $q_2$ mengarah ke kanan atas. Dengan demikian jelas terlihat bahwa gaya elektrostatik pada kedua muatan merupakan gaya tolak-menolak.
Selanjutnya bagaimana bila $q_1 = +3 \ {\rm nC}$ dan $q_2 = -3 \ {\rm nC}$? Kedua muatan berbeda tanda. Vektor-vektor posisi relatif dan vektor-vektor satuan untuk kedua muatan kembali diperoleh dari Persamaan \eqref{eqn:r12} dan \eqref{eqn:r12-unit} untuk $\vec{F} _{12}$ dan dari Persamaan \eqref{eqn:r21} dan \eqref{eqn:r21-unit} untuk $\vec{F} _{21}$. Dapat diperoleh
\begin{equation}\label{eqn:f12-case-2} \begin{array}{rcl} \vec{F} _{12} & = & \displaystyle k \frac{q_1 q_2}{r _{12}^2} \hat{r} _{12} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+3 \ {\rm n})(-3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right] \end{array} \end{equation}
dan
\begin{equation}\label{eqn:f21-case-2} \begin{array}{rcl} \vec{F} _{21} & = & \displaystyle k \frac{q_2 q_1}{r _{21}^2} \hat{r} _{21} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(-3 \ {\rm n})(+3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{-\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right]. \end{array} \end{equation}
Kembali digunakan cara penulisan dalam bentuk $\rm(\color{#f90}{besar})[\color{#0b5}{arah}]$ untuk Persamaan \eqref{eqn:f12-case-2} dan \eqref{eqn:f21-case-2} yang akan memudahkan pemilahan informasi besar dan arah dari kedua gaya.

Gambar 6. Dua buah muatan berbeda tanda dan gaya yang bekerja pada masing-masing muatan akibat adanya muatan lain.
Arah kedua gaya pada Persamaan \eqref{eqn:f12-case-2} dan \eqref{eqn:f21-case-2} disajikan dalam Gambar 6, dengan gaya pertama yang bekerja muatan $q_1$ mengarah ke kanan atas dan gaya kedua yang bekerja pada muatan $q_2$ mengarah ke kiri bawah. Gaya pada kedua muatan merupakan gaya tarik-menarik sebagaimana terlihat pada Gambar 6.
Kasus lain adalah bila $q_1 = -3 \ {\rm nC}$ dan $q_2 = -3 \ {\rm nC}$ atau kedua muatan bertanda sama dengan tandanya negatif. Dengan cara yang sama, vektor-vektor posisi relatif dan vektor-vektor satuan untuk kedua muatan diperoleh dari Persamaan \eqref{eqn:r12} dan \eqref{eqn:r12-unit} untuk $\vec{F} _{12}$ dan dari Persamaan \eqref{eqn:r21} dan \eqref{eqn:r21-unit} untuk $\vec{F} _{21}$. Perhitungan yang dilakukan akan memberikan
\begin{equation}\label{eqn:f12-case-3} \begin{array}{rcl} \vec{F} _{12} & = & \displaystyle k \frac{q_1 q_2}{r _{12}^2} \hat{r} _{12} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(-3 \ {\rm n})(-3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ -\frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{-\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right] \end{array} \end{equation}
dan
\begin{equation}\label{eqn:f21-case-3} \begin{array}{rcl} \vec{F} _{21} & = & \displaystyle k \frac{q_2 q_1}{r _{21}^2} \hat{r} _{21} \newline & = & \displaystyle (9 \ {\rm G}) \frac{(-3 \ {\rm n})(-3 \ {\rm n})}{(3\sqrt{2} \ {\rm \mu})^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & \displaystyle 4.5 \frac{\rm G n^2}{\rm \mu^2} \left[ \frac12 \sqrt{2} (\hat{x} + \hat{y}) \right] \newline & = & (\color{#f90}{4.5 \times 10^3}) \left[ \color{#0b5}{\frac12 \sqrt{2} (\hat{x} + \hat{y})} \right]. \end{array} \end{equation}
Untuk memudahkan untuk memilah informasi besar dan arah kedua gaya bila, Persamaan \eqref{eqn:f12-case-3} dan \eqref{eqn:f21-case-3} ditulikan dalam bentuk $\rm(\color{#f90}{besar})[\color{#0b5}{arah}]$.
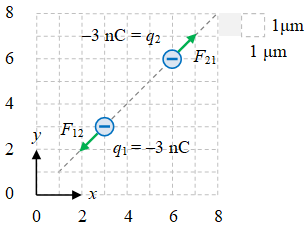
Gambar 7. Dua buah muatan negatif dan gaya yang bekerja pada masing-masing muatan akibat adanya muatan lain.
Terlihat bahwa gaya elektrostatik pada kedua muatan merupakan gaya tolak-menolak sebagaimana diilustrasikan pada Gambar 7. Arah gaya yang bekerja pada muatan $q_1$ yang diberikan oleh Persamaan \eqref{eqn:f12-case-3} tergambarkan ke arah kiri bawah, sedangkan pada muatan $g_2$ yang diberikan oleh Persamaan \eqref{eqn:f21-case-3} tergambarkan ke arah kanan atas.
Dengan demikian dapat disarikan dari Gambar 5, 6, dan 7 bahwa
Selanjutnya kedua persamaan, yaitu Persamaan \eqref{eqn-electrostatic-force-two-point-charges} dan \eqref{eqn-electrostatic-force-two-point-charges-vector} memberikan hasil yang sama, akan tetapi Persamaan \eqref{eqn-electrostatic-force-two-point-charges} membutuhkan informasi arah gaya dari tanda kedua muatan, sedangkan Persamaan \eqref{eqn-electrostatic-force-two-point-charges-vector} telah menyimpan informasi arah gaya pada kedua muatan di dalam formulasinya.
Terdapat pula penulisan gaya Coulomb yang tidak menggunakan indeks untuk gaya dan jarak antar kedua muatan, serta hanya indeks $1$ dan $2$ untuk kedua muatannya sehingga amat ringkas bentuknya [13, 14]
\begin{equation}\label{eqn-coulomb-force-basic-form} F = k \frac{q_1 q_2}{r^2}, \end{equation}
dengan pengertian arah gaya antar kedua muatan, tarik-menarik atau tolak-menolak, perlu dipahami terlebih dahulu terkait dengan jenis kedua muatan (keduanya positif, positif-negatif, atau keduanya negatif). Persamaan \eqref{eqn-coulomb-force-basic-form} ini tepat bila hanya ingin menghitung besar gaya antar dua muatan, akan tetapi bila terdapat lebih dari dua muatan, perumusan ini dapat menjadi lebih merepotkan ketimbang perumusan dengan notasi vektor pada Persamaan \eqref{eqn-electrostatic-force-two-point-charges-vector}.
Gaya elektrostatik yang diungkapkan oleh hukum Coulomb juga berlaku untuk disribusi muatan, atau muatan yang ukurannya (dan juga bentuknya) perlu dipertimbankang, yang secara teknis dilakukan menggunakan bentuk integral [15].
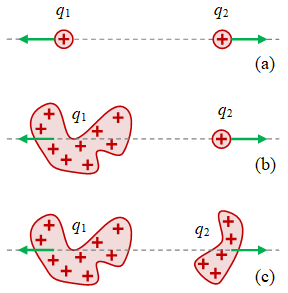
Gambar 8. Gaya elektrostatik antara: (a) dua muatan titik; (b) muatan titik dengan distribusi muatan, dan (c) distribusi muatan dengan distribusi muatan.
Tabel 1. Tiga kemungkinan interaksi bila sumber muatan dapat berbentuk muatan titik atau distribusi muatan.
| Gambar 8 | $q_1$ | $q_2$ | $\vec{F}_{21}$ |
|---|---|---|---|
| (a) | muatan titik |
muatan titik |
$\displaystyle k \frac{q_2 q_1}{r_{21}^2} \hat{r}_{21}$ |
| (b) | distribusi muatan |
muatan titik |
$\displaystyle \int k \frac{q_2 dq_1}{r_{21}^2} \hat{r}_{21}$ |
| (c) | distribusi muatan |
distribusi muatan |
$\displaystyle \int \int k \frac{dq_2 dq_1}{r_{21}^2} \hat{r}_{21}$ |
Persamaan \eqref{eqn-electrostatic-force-two-point-charges}, \eqref{eqn-electrostatic-force-two-point-charges-vector}, dan \eqref{eqn-coulomb-force-basic-form} hanya mengakomodasi bila dua benda yang bermuatan berbentuk muatan titik. Akan tetapi benda yang berinteraksi dapat pula berbentuk distribusi muatan. Kemungkinan interaksi antar dua benda yang dapat berbentuk muatan titik atau distribusi muatan diberikan pada Gambar 8 dan formulasi gaya elektrostatik terkaitnya diberikan pada Tabel 1. Sebagi contohnya diambil gaya pada muatan $q_2$ akibat adanya muatan $q_1$ yang berada di sebelah kanan pada Gambar 8.
Untuk pembahasan ini istilah gaya elektrostatik bila terkait dengan hukum Coulomb dirasakan lebih tepat, walaupun diskusi mengenai kedua istilah gaya listrik dan gaya elektrostatik belum konklusif [16].
— Sparisoma Viridi (@6unpnp) January 12, 2022
electric charge • electric field • electric potential