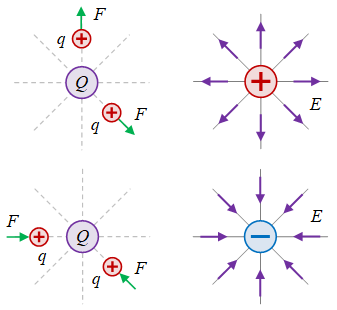
Gambar 1. Pengukuran gaya listrik $F$ pada muatan uji (kiri) dan hasil medan listriknya $E$ (kanan).
Medan listrik merupakan suatu properti kelistikan yang melekat pada setiap titik dalam ruang saat terdapatnya muatan dalam bentuk apapun [1]. Konsep medan listrik muncul dalam upaya untuk menjelaskan gaya-gaya yang dapat berinteraksi pada jarak jauh, di mana semua benda bermuatan menciptakan medan listrik yang meluas keluar dari muatan ke ruang di sekelilingnya [2]. Dengan konsep ini hukum Coulomb yang menjelaskan gaya antara dua muatan yang terpisahkan jarak dapat direformulasi dalam dua langkah terpisah [3]. Sebagai suatu besaran vektor medan listrik dapat divisualisasikan dengan panah mengarah ke atau berasal dari muatan-muatan, yaitu masuk secara radial ke muatan negatif dan keluar secara radial dari muatan positif [4]. Benda bermuatan penyebab medan listrik dapat berupa titik muatan, sejumlah titik muatan, silinder bermuatan, bolah bermuatan, dan pelat paralel bermuatan [5]. Medan listrik ini berperan penting dalam banyak bidang fisika dan dieksploitasi secara praktis dalam teknologi kelistrikan [6].
Medan listrik didefinisikan gaya listrik per satuan muatan. Untuk mengukur medan listrik suatu muatan $Q$, yang disebut sebagai muatan sumber, perlu diletakkan suatu muatan uji $q$ pada jarak $r$ dari muatan sumber tersebut. Gaya elektrostatik yang bekerja pada muatan uji $q$ akibat adanya muatan sumber $Q$ diukur sebagai $\vec{F}$ dan medan listrik didefinisikan sebagai
\begin{equation}\label{eqn:electric-field-definition} \vec{E} = \frac{\vec{F}}{q}. \end{equation}
Sebagai muatan uji selalu digunakan muatan bertanda positif. Ilustrasi proses untuk mendapatkan medan listrik $\vec{E}$ dari gaya elektrostatik $\vec{F}$ diberikan pada gambar berikut.

Gambar 1. Pengukuran gaya listrik $F$ pada muatan uji (kiri) dan hasil medan listriknya $E$ (kanan).
Mula-mula terdapat muatan sumber $Q$ yang belum diketahui tandanya. Lalu muatan uji positif $q$ diletakkan pada jarak tertentu dari muatan sumber dan gaya elektrostatiknya $\vec{F}$ diukur. Berulang-ulang hal ini dilakukan pada jarak berbeda dan pada arah berbeda dari muatan sumber. Nilai-nilai $\vec{F}$ ini kemudian dibagi dengan nilai muatan uji sehingga diperoleh $\vec{E}$, sebagaimana diilustrasikan pada Gambar 1.
Untuk suatu muatan titik, yang ilustrasinya telah diberikan pada Gambar 1, gaya elektrostatik pada jarak $r$ dari muatan sumber diberikan oleh
\begin{equation}\label{eqn:electrostatic-force-source-charge} \vec{F} = k \frac{Qq}{r^2} \ \hat{r}, \end{equation}
sehingga dengan menggunakan Persamaan \eqref{eqn:electric-field-definition} akan diperoleh
\begin{equation}\label{eqn:electric-field-source-charge} \vec{E} = k \frac{Q}{r^2} \ \hat{r}, \end{equation}
yang merupakan medan listrik oleh satu muatan titik. Setelah konsep medan listrik menghasilkan Persamaan \eqref{eqn:electric-field-source-charge}, rumusan ini dapat dibuat umum bila terdapat muatan $q_i$ yang terletak di pusat koordinat, maka di sekelilingnya akan terdapat medan listrik
\begin{equation}\label{eqn:electric-field-qi-origin} \vec{E}_i = k \frac{q_i}{r^2} \ \hat{r}. \end{equation}
Bila muatan $q_i$ tidak terletak di pusat koordinat melainkan pada posisi $\vec{r}_i$ maka Persamaan \eqref{eqn:electric-field-qi-origin} akan menjadi
\begin{equation}\label{eqn:electric-field-qi-general} \vec{E}_i(\vec{r}) = k \frac{q_i}{|\vec{r} - \vec{r}_i|^3} \ (\vec{r} - \vec{r}_i), \end{equation}
yang merupakan bentuk yang lebih umum untuk medan listrik pada posisi sembarang $\vec{r}$.
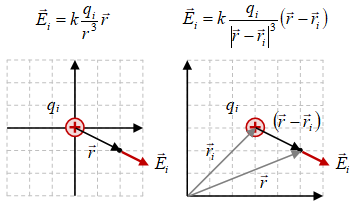
Gambar 2. Medan listrik $\vec{E}_i$ di posisi $\vec{r}$ akibat muatan $q_i$ yang terletak di: pusat koordinat (kiri) dan posisi sembarang $\vec{r}_i$ (kanan)
Bagian kanan dari Gambar 2 akan menjadi bagian kiri saat digunakan $\vec{r}_i = 0$ atau muatan $q_i$ terletak di pusat koordinat. Dengan demikian Persamaan \eqref{eqn:electric-field-qi-origin} merupakan bentuk khusus dari Persamaan \eqref{eqn:electric-field-qi-general}.
Dari Gambar 2 dan Persaamaan Persamaan \eqref{eqn:electric-field-qi-origin} dan \eqref{eqn:electric-field-qi-general} dapat disimpulkan bahwa jarak relatif dari titik amat, tempat di mana medan listrik ingin dihitung, terhadap ke muatan penyebab medan listrik adalah yang diperlukan. Informasi posisi muatan dan titik amat digunakan untuk mendapatkan posisi relatif tersebut dan juga vektor satuan terkait. Ilustrasi hal ini secara numerik diberikan pada gambar berikut.
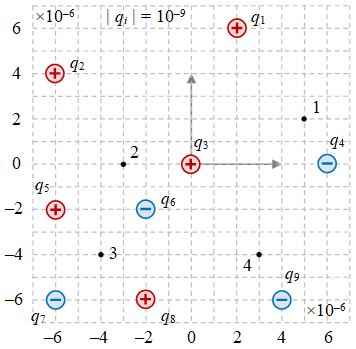
Gambar 3. Terdapat sembilan muatan titik dan empat posisi tempat medan listriknya ingin diketahui.
Misalkan ingin dicari medan listrik $\vec{E}_1(\vec{r}_1)$ atau medan listrik pada titik $1$ akibat muatan $q_1 = 10^{-9} \ {\rm C}$ dan $\vec{E}_2(\vec{r}_2)$ atau medan listrik pada titik $2$ akibat muatan $q_2 = 10^{-9} \ {\rm C}$, yang jarak relatif titik amat dari muatan penyebab medan listrik adalah sama. Satu grid pada Gambar 3 berukuran $10^{-6} \ {\rm m} \times 10^{-6} \ {\rm m}$.
Dari Gambar 3 dapat diperoleh
\begin{equation}\label{eqn-rq1} \vec{r} _{q1} = (2\hat{x} + 6\hat{y}) \ {\rm \mu m}, \end{equation}
\begin{equation}\label{eqn-rq2} \vec{r} _{q2} = (-6\hat{x} + 4\hat{y}) \ {\rm \mu m}, \end{equation}
\begin{equation}\label{eqn-r1} \vec{r}_1 = (5\hat{x} + 2\hat{y}) \ {\rm \mu m}, \end{equation}
\begin{equation}\label{eqn-r2} \vec{r}_2 = (-3\hat{x}) \ {\rm \mu m}, \end{equation}
yang akan membantu untuk mendapatkan
\begin{equation}\label{eqn-r1-rq1} \begin{array}{rcl} \vec{r}_1 - \vec{r} _{q1} & = & \left[ (5\hat{x} + 2\hat{y}) - (2\hat{x} + 6\hat{y}) \right] \ {\rm \mu m} \newline & = & (3\hat{x} - 4 \hat{y}) \ {\rm \mu m}, \newline | \vec{r}_1 - \vec{r} _{q1} | & = & 5 \ {\rm \mu m} \end{array} \end{equation}
dan
\begin{equation}\label{eqn-r2-rq2} \begin{array}{rcl} \vec{r}_2 - \vec{r} _{q2} & = & \left[ (-3\hat{x}) - (-6\hat{x} + 4\hat{y}) \right] \ {\rm \mu m} \newline & = & (3\hat{x} - 4 \hat{y}) \ {\rm \mu m}, \newline | \vec{r}_2 - \vec{r} _{q2} | & = & 5 \ {\rm \mu m}. \end{array} \end{equation}
Menggunakan Persamaan \eqref{eqn:electric-field-qi-general} dapat diperoleh
\begin{equation}\label{eqn-e1} \begin{array}{rcl} \vec{E}_{q1}(\vec{r}_1) & = & \displaystyle k \frac{q_1}{| \vec{r}_1 - \vec{r} _{q1} |^3} \ (\vec{r}_1 - \vec{r} _{q1}) \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+1 \ {\rm n})}{(5 \ {\rm \mu})^3} \ (3\hat{x} - 4 \hat{y}) \ {\rm \mu N/C} \newline & = & 360 \ (0.6\hat{x} - 0.8\hat{y}) \ {\rm GN/C} \end{array} \end{equation}
dan
\begin{equation}\label{eqn-e2} \begin{array}{rcl} \vec{E}_{q2}(\vec{r}_2) & = & \displaystyle k \frac{q_2}{| \vec{r}_2 - \vec{r} _{q2} |^3} \ (\vec{r}_2 - \vec{r} _{q2}) \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+1 \ {\rm n})}{(5 \ {\rm \mu})^3} \ (3\hat{x} - 4 \hat{y}) \ {\rm \mu N/C} \newline & = & 360 \ (0.6\hat{x} - 0.8\hat{y}) \ {\rm GN/C}, \end{array} \end{equation}
yang keduanya memberikan hasil yang sama. Persamaan \eqref{eqn-e1} dan \eqref{eqn-e2} dapat dituliskan menjadi
\begin{equation}\label{eqn-e-mag-dir-unit} \vec{E} = \color{#f60}{360} \ (\color{#6d0}{0.6\hat{x} - 0.8\hat{y}}) \ {\rm \color{#07c}{GN/C}}, \end{equation}
yang merupakan bentuk $\rm \color{#f60}{besar} \ (\color{#6d0}{arah}) \ \color{#07c}{satuan}$. Dengan format penulisan pada Persamaan \eqref{eqn-e-mag-dir-unit} ini informasi mudah diperoleh, misalnya
besar medan listrik adalah
\begin{equation}\label{eqn-e-mag-unit} E = \color{#f60}{360} \ {\rm \color{#07c}{GN/C}} \end{equation}
yang didapatkan hanya dengan menghilang vektor satuan yang merupakan arah dan untuk mendapatkan arahnya dapat dilakukan
\begin{equation}\label{eqn-e-dir} \tan \theta = \frac{(\color{#6d0}{0.6\hat{x} - 0.8\hat{y}}) \cdot \hat{y}}{(\color{#6d0}{0.6\hat{x} - 0.8\hat{y}}) \cdot \hat{x}} \end{equation}
menggunakan operator perkalian titik dua buah vektor.
Bagaimana bila pada suatu titik dalam ruang ingin dihitung medan listrik akibat dua buah muatan listrik? Dikarenakan medan listrik merupakan besaran vektor, maka medan listrik total di titik tersebut adalah jumlah medan listrik pada titik tersebut oleh masing-masing muatan.
Bila terdapat $N$ buah muatan dengan muatan $q_i$ terletak pada $\vec{r}_{qi}$ maka
\begin{equation}\label{eqn-e-total} \vec{E}(\vec{r}) = \sum _{i = 1} ^N \vec{E} _{qi} (\vec{r}) \end{equation}
adalah medan listrik total pada posisi $\vec{r}$, yang menggunakan Persamaan \eqref{eqn:electric-field-qi-general} untuk suku di dalam somasinya.
Sebagai contoh, dengan merujuk pada Gambar 3, pada titik $3$ atau $(-4 \ {\rm \mu m}, -4 \ {\rm \mu m})$ ingin dicari medan listrik akibat $q_5 = +1 \ {\rm nC}$ dan $q_7 = -1 \ {\rm nC}$ yang masing-masing bertempat pada posisi $(-6 \ {\rm \mu m}, -2 \ {\rm \mu m})$ dan $(-6 \ {\rm \mu m}, -6 \ {\rm \mu m})$.
Posisi relatif titik amat terhadap kedua muatan sumber medan listrik adalah
\begin{equation}\label{eqn-r3-rq5} \begin{array}{rcl} \vec{r}_3 - \vec{r} _{q5} & = & \left[ (-4\hat{x} + -4\hat{y}) - (-6\hat{x} - 2\hat{y}) \right] \ {\rm \mu m} \newline & = & (2\hat{x} - 2 \hat{y}) \ {\rm \mu m}, \newline | \vec{r}_3 - \vec{r} _{q5} | & = & 2\sqrt{2} \ {\rm \mu m} \end{array} \end{equation}
dan
\begin{equation}\label{eqn-r3-rq7} \begin{array}{rcl} \vec{r}_3 - \vec{r} _{q7} & = & \left[ (-4\hat{x} + -4\hat{y}) - (-6\hat{x} - 6\hat{y}) \right] \ {\rm \mu m} \newline & = & (2\hat{x} + 2 \hat{y}) \ {\rm \mu m}, \newline | \vec{r}_3 - \vec{r} _{q7} | & = & 2\sqrt{2} \ {\rm \mu m}. \end{array} \end{equation}
Selanjutnya dengan kembali memanfaatkan Persamaan \eqref{eqn:electric-field-qi-general} akan didapatkan
\begin{equation}\label{eqn-eq5-r3} \begin{array}{rcl} \vec{E}_{q5}(\vec{r}_3) & = & \displaystyle k \frac{q_5}{| \vec{r}_3 - \vec{r} _{q5} |^3} \ (\vec{r}_3 - \vec{r} _{q5}) \newline & = & \displaystyle (9 \ {\rm G}) \frac{(+1 \ {\rm n})}{(2\sqrt{2} \ {\rm \mu})^3} \ (2\hat{x} - 2 \hat{y}) \ {\rm \mu N/C} \newline & = & 1125 \ \left(\frac12\sqrt{2}\hat{x} - \frac12\sqrt{2}\hat{y}\right) \ {\rm GN/C} \end{array} \end{equation}
dan
\begin{equation}\label{eqn-eq7-r3} \begin{array}{rcl} \vec{E}_{q7}(\vec{r}_3) & = & \displaystyle k \frac{q_7}{| \vec{r}_3 - \vec{r} _{q7} |^3} \ (\vec{r}_3 - \vec{r} _{q7}) \newline & = & \displaystyle (9 \ {\rm G}) \frac{(-1 \ {\rm n})}{(2\sqrt{2} \ {\rm \mu})^3} \ (2\hat{x} + 2 \hat{y}) \ {\rm \mu N/C} \newline & = & 1125 \ \left(-\frac12\sqrt{2}\hat{x} - \frac12\sqrt{2}\hat{y}\right) \ {\rm GN/C}. \end{array} \end{equation}
Selanjutnya dengan Persamaan \eqref{eqn-e-total} dapat diperoleh
\begin{equation}\label{eqn-eq5+eq7-r3} \begin{array}{rcl} \vec{E} _{q5 + q7}(\vec{r}_3) & = & \vec{E} _{q5}(\vec{r}_3) + \vec{E} _{q7}(\vec{r}_3) \newline & = & \left[ 1125 \ \left(\frac12\sqrt{2}\hat{x} - \frac12\sqrt{2}\hat{y}\right) \right. \newline && + \left. 1125 \ \left(-\frac12\sqrt{2}\hat{x} - \frac12\sqrt{2}\hat{y}\right) \right] \ {\rm GN/C} \newline & = & 1125 \ \left( -\sqrt{2}\hat{y}\right) \ {\rm GN/C} \newline & = & \color{#f60}{1125\sqrt{2}} \ (\color{#6d0}{-\hat{y}}) \ {\rm \color{#07c}{GN/C}}, \end{array} \end{equation}
yang merupakan medan listrik total di titik $3$ akibat muatan $q_5$ dan $q_7$.
— Sparisoma Viridi (@6unpnp) January 12, 2022
electric charge • electrostatic force • electric potential