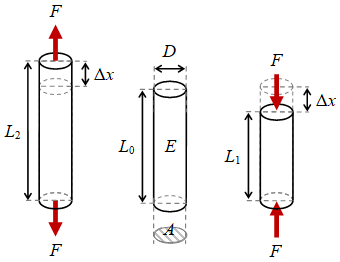
Gambar 1. Benda bertambah panjang saat ditarik (kiri), panjang mula-mula (tengah), dan bertambah pendek saat ditekan (kanan), sehingga $L_2 > L_0 > L_1$.
Modulus Young suatu bahan merupakan sifat mendasar setiap bahan yang tidak dapat diubah, akan tetapi bergantung pada temperatur dan tekanan, dan merupakan inti dari sifat kekuatan suatu bahan [1]. Kontanta numerik ini mendeskripsikan sifat elastik suatu bahan padatan saat mengalami penarikan atau penekanan hanya dalam satu arah, biasanya pada arah panjang atau dimensi yang paling besar dari suatu bahan, dan kadang disebut pula sebagai modulus elastisitas [2]. Modulus ini didefinsikan sebagai rasio dari tegangan tarik (tensile stress) dan regangan tarik [3]. Nilai modulus Young secara umum bernilai begitu besar sehingga tidak dinyatakan dalam pascal akan tetapi dalam gigapascal atau $\rm GPa$ [4], seperti dari sekitar $0.01 - 0.1 \ \rm GPa$ untuk karet dengan regangan kecil sampai $1220 \ \rm GPa$ untuk intan [5]. Penguran modulus elastik dapat dilakukan dengan menggunakan cara statis dan dinamis [6].
Modulus Young $E$ diperoleh melalui
\begin{equation}\label{eqn-youngs-modulus} E = \frac{\sigma}{\varepsilon}, \end{equation}
yang memerlukan tegangan tarik $\sigma$
\begin{equation}\label{eqn-tensile-stress} \sigma = \frac{F}{A} \end{equation}
dan regangan tarik $\varepsilon$
\begin{equation}\label{eqn-tensile-strain} \varepsilon = \frac{\Delta x}{L_0}, \end{equation}
dengan $F$ gaya tarik, $A$ luas penampang, $\Delta x$ pertambahan panjang, dan $L_0$ panjang mula-mula. Pengukuran modulus Young umumnya dilakukan dengan penarikan dikarenakan lebih mudah ketimbang penekanan. Seharusnya kedua proses memberikan hasil yang sama sebagaimana diilustrasikan pada Gambar 1.

Gambar 1. Benda bertambah panjang saat ditarik (kiri), panjang mula-mula (tengah), dan bertambah pendek saat ditekan (kanan), sehingga $L_2 > L_0 > L_1$.
Walaupun proses penarikan lebih umum dalam mengukur modulus Young $E$, akan tetapi menurut perumusan pada Persamaan \eqref{eqn-youngs-modulus} pemberian penarikan atau penekanan seharusnya memberikan hasil yang sama, walau yang kedua umumnya lebih sulit dalam penerapan teknisnya saat pengukuran. Ilustrasi bahwa kedua proses akan memberikan hasil yang sama secara teori diberikan pada Gambar 1.
Beberapa nilai modulus Young diberikan pada tabel berikut.
Tabel 1. Beberapa nilai modulus Young, yield strength, dan ultimate strength [5].
| Bahan | $E$ ($\rm GPa$) |
$\sigma_u$ ($\rm MPa$) |
$\sigma_y$ ($\rm MPa$) |
|---|---|---|---|
| ABS plastics | 1.4 - 3.1 | 40 | |
| Acrylic | 3.2 | 70 | |
| Aluminium | 69 | 110 | 95 |
| Aluminum Bronze 120 | |||
| Copper | 117 | 220 | 70 |
| Bronze | 96 - 120 | ||
| Cadmium | 32 | ||
| Gold | 74 | ||
| Granite | 52 | ||
| Graphene | 1000 | ||
| Grey Cast Iron | 130 | ||
| Glass | 50 - 90 | 50 (c) | |
| Iron | 210 | ||
| Lead | 13.8 | ||
| Nickel | 170 | ||
| Nickel Silver | 128 | ||
| Nickel Steel | 200 | ||
| Nylon-6 | 2 - 4 | 45 - 90 | 45 |
| Platinum | 147 | ||
| Rubber (st) | 0.01 - 0.1 | ||
| Silver | 72 | ||
| Steel, stainless AISI 302 | 180 | 860 | 502 |
| Tungsten (W) | 400 - 410 | ||
| Tungsten Carbide (WC) | 450 - 650 |
st: small strain (regangan kecil), c: compression (penekanan).
Selain penggunaaan $E$ untuk modulus Young, $\sigma_y$ untuk yield stress, dan $\sigma_u$ untuk ultimate strength [7] pada Tabel 1, dapat pula digunakan $Re$ untuk yield stress, dan $Rm$ untuk ultimate strength [8].
Dalam experimen, umumnya $F$ diberikan dalam bentuk penarikan oleh suatu alat atau dengan menggantungkan suatu benda dengan massa tertentu $m$. Selanjutnya diukur pertambahan panjang $\Delta x$ untuk setiap penambahan massa $\Delta m$. Pada pelaksanaannya pengukuran $\Delta x$ tidak semudah seperti terlihat pada Gambar 1 yang hanya menggunakan satu kawat, kadang diperlukan juga dua kawat dengan salah satu kawat sebagai pembanding [9].
Dari hasil yang diperoleh dapat dibuat grafik antara tegangan tarik $\sigma$ dengan regangan tarik $\varepsilon$ untuk melihat apakah suatu bahan menunjukkan elastisitas [10]. Dan seringkali terjadi bahwa hasil eksperiman menghasilkan nilai yang amat jauh dengan data yang diberikan dari buku rujukan [11].
Sejumlah data buatan disajikan untuk menjadi bahan ilustrasi dalam mementukan modulus Young melalui eksperimen uji tarik.
Tabel 2. Beberapa nilai modulus Young $E$ dan mass jenis $\rho$ beberapa bahan.
| Bahan | $E$ ($\rm GPa$) |
$\rho$ ($\rm g/cm^3$) |
|---|---|---|
| Aluminium | 69 | 2.7 |
| Copper | 117 | 8.96 |
| Bronze | 100 | 8.73 |
| Iron | 210 | 7.87 |
| Lead | 13.8 | 11.3 |
| Nickel | 170 | 8.90 |
| Silver | 72 | 10.5 |
| SS 302 | 180 | 7.9 |
| Tungsten | 405 | 19.3 |
Terdapat beberapa gulung kawat yang panjangnya sekitar $50 \ \rm m$ pada tiap gulungnya. Massa setiap gulung, dalam kilogram, adalah sebagai berikut.
Tabel 3. Massa gulungan kawat dengan panjang $50 \rm m$ yang berdiameter $2 \rm mm$.
| $\rm M1$ | $\rm M2$ | $\rm M3$ | $\rm M4$ | $\rm M5$ | $\rm M6$ | $\rm M7$ | $\rm M8$ | $\rm M9$ |
| 0.42 | 1.41 | 1.37 | 1.24 | 1.78 | 1.40 | 1.65 | 1.24 | 3.03 |
Kode bahan diberikan sebagai $\rm M1 - M9$. Setiap bahan diuji tarik dengan salah satu metode pengukuran elastisitas untuk diperoleh modulus Youngnya. Dari hasil pengukuran dapat dibuat grafik antara tegangan tarik $\sigma$ dan regangan tarik $\varepsilon$.
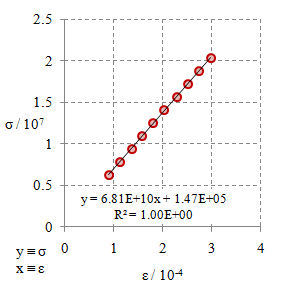
Gambar 2. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M1$.
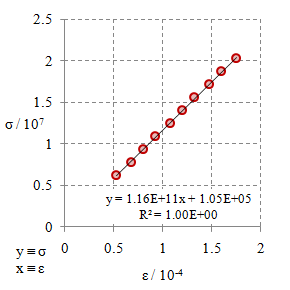
Gambar 3. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M2$.
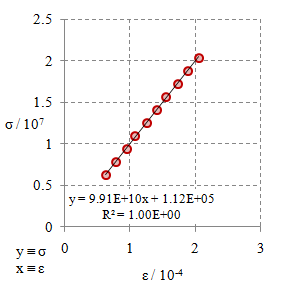
Gambar 4. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M3$.
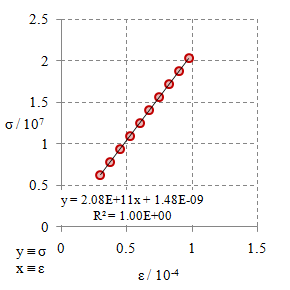
Gambar 5. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M4$.
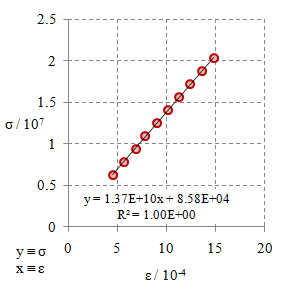
Gambar 6. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M5$.
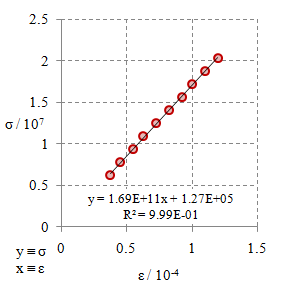
Gambar 7. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M6$.
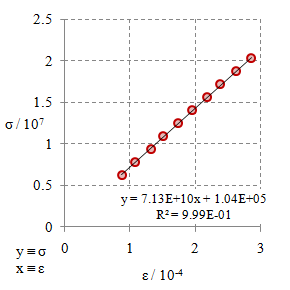
Gambar 8. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M7$.
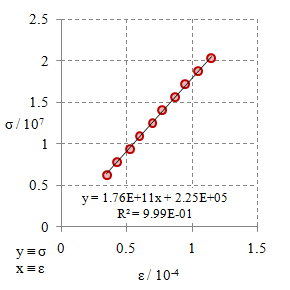
Gambar 9. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M8$.
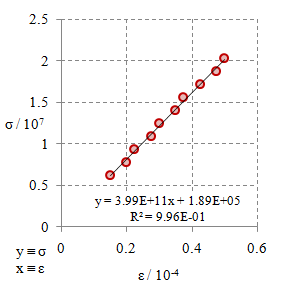
Gambar 10. Kurva tegangan tarik $\sigma$ terhadap regangan tarik $\varepsilon$ untuk bahan $\rm M9$.
Dari Gambar 2 - 10 dengan menggunakan persamaan
\begin{equation}\label{eqn-stress-strain-e} \sigma = E \varepsilon + {\rm err}, \end{equation}
dengan $\rm err$ adalah kesalahan, di mana hasil yang baik konstanta ini seharusnya bernilai nol. Dalam beberapa aplikasi untuk menghasilkan kurva regresi linier sering kali ditampilkan secara otomatis garis yang mengikuti persamaan
\begin{equation}\label{eqn-linear-regression} y = ax + b, \end{equation}
yang dalam hal ini $y \equiv \sigma$, $a \equiv E$, $x \equiv \varepsilon$, dan $b \equiv \rm err$ agar sesuai dengan Persamaan \eqref{eqn-stress-strain-e}.
Secara empirik dapat dibuah hubungan antara modulus Young $E$ dan rapat massa $\rho$ untuk beberapa jenis bahan, yang diberikan hanya sebagai ilustrasi.
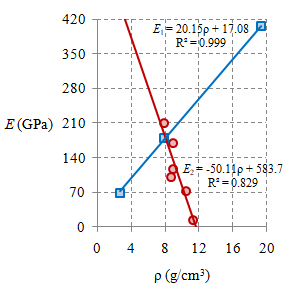
Gambar 11. Kurva antara modulus Young $E$ dan rapat massa $\rho$ untuk berbagai jenis bahan.
Terlihat bahwa untuk bahan-bahan yang disampaikan tidak terdapat satu hubungan yang linier antara modulus Young $E$ dan rapat massa $\rho$ dan dapat dipisahkan dalam dua buah kelompok sehingga terdapat hubungan linier seperti diberikan pada Gambar 11. Dalam kelompok pertama ($\color{#07c}{\square}$) semakin besar $\rho$ akan semakin besar $E$, sedangkan dalam kelompok kedua ($\color{#c00}{\Large \circ}$) semakin besar $\rho$ akan semakin kecil $E$. Jumlah bahan untuk kelompok pertama adalah tiga dan kelompok kedua adalah enam.
elasticity • shear modulus • bulk modulus