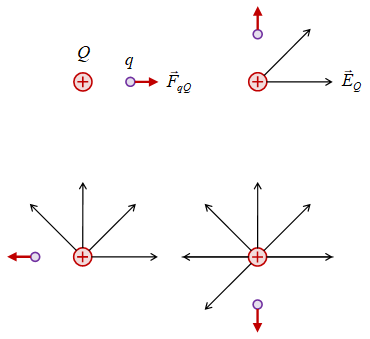
Gambar 1. Gaya elektrotatik $\vec{F}_{qQ}$ oleh muatan sumber $Q$ pada muatan uji $q$ di berbagai posisi.
Antar dua benda bermuatan terdapat interaksi berupa gaya elektrostatik yang dideskripsikan oleh hukum Coulomb [1]. Garis-garis medan listrik yang disebabkan oleh sebuah muatan listrik merupakan lintasan yang akan dilalui oleh muatan uji yang semula diam, saat diletakkan dalam pengaruh medan listrik tersebut [2]. Agar muatan uji berubah keadaan geraknya dari diam menjadi bergerak mengikuti garis-garis medan listrik memerlukan gaya, gaya ini yang disebut sebagai gaya elektrostatik atau gaya listrik. Potensi suatu medan listrik untuk membuat muatan uji bergerak menempuh garis-garis gaya listrik disebut sebagai potensial listrik [3]. Hubungan gaya gaya elektrostatik antar muatan sumber dan muatan uji dengan medan listrik yang disebabkan muatan sumber, dan hubungan antara medan listrik dengan potensial listrik akan disajikan secara ringkas di ini.
Sebuah muatan sumber $Q$ memberikan gaya elektrostatik $\vec{F}_{qQ}$ pada muatan uji $q$ sebagaimana diberikan pada Gambar 1.

Gambar 1. Gaya elektrotatik $\vec{F}_{qQ}$ oleh muatan sumber $Q$ pada muatan uji $q$ di berbagai posisi.
Saat muatan uji $q$ berada pada suatu posisi gaya yang dialaminya $\vec{F}_{qQ}$, dicatat arahnya dan digambarkan. Posisi muatan uji kemudian diubah dan pada posisi baru hal yang sama dilakukan, arahnya dicatat dan digambarkan. Demikian seterusnya sehingga dalam ruang di sekitar muatan sumber dapat digambarkan garis-garis medan lisrik yang disebabkannya. Medan listrik yang disebabkan oleh muatan sumber diperoleh dari
\begin{equation}\label{eqn:electric-field-from-electrostatic-force} \vec{E}_Q = \frac{\vec{F} _{qQ}}{q}, \end{equation}
dengan $q > 0$, yang akan memberikan ungkapan
\begin{equation}\label{eqn:electric-field-point-charge} \vec{E}_Q(\vec{r}) = k \frac{Q}{r^2} \ \hat{r} = k \frac{Q}{|\vec{r}|^3} \ \vec{r}, \end{equation}
sebagai medan listrik, yang disebabkan oleh muatan sumber berupa muatan titik yang terletak pada pusat kooordinat, pada sembarang posisi $\vec{r} = r\hat{r}$, dengan $r = |\vec{r}|$. Pada Persamaan \eqref{eqn:electric-field-point-charge} suku di ruas tengah sama dengan suku di ruas kanan. Alasan mengapa suku di ruas kanan dituliskan adalah agar jelas bahwa medan listrik \vec{E} merupakan fungsi dari vektor posisi $\vec{r}$, yaitu $\vec{E} = \vec{E}(\vec{r})$. Untuk selanjutnya akan dituliskan
\begin{equation}\label{eqn:electric-field-point-charge-simple} \vec{E} = k \frac{q}{r^2} \ \hat{r}, \end{equation}
untuk menyederhanakan penulisan dari Persamaan \eqref{eqn:electric-field-point-charge}.
Potensial listik pada suatu posisi adalah potensi yang tersimpan pada titik itu untuk menggerakkan muatan uji mengikuti garis-garis medan listrik melalui gaya listrik. Pontensial listrik terkait dengan gaya listrik melalui
\begin{equation}\label{eqn:electric-potential-from-electric-field} V = - \int \vec{E} \cdot d\vec{r}, \end{equation}
dengan $d\vec{s}$ adalah elemen lintasan. Indeks muatan sumber $Q$ tidak lagi digunakan pada Persamaan \eqref{eqn:electric-potential-from-electric-field} untuk menyederhanakan penulisan, juga informasi bahwa medan listrik $\vec{E}$ merupakan fungsi dari posisi $\vec{r}$, yaitu $\vec{E} = \vec{E}(\vec{r})$. Untuk potensial listrik oleh muatan titik, suatu posisi jarak jauh tak-hingga umumnya digunakan sebagai referensi
\begin{equation}\label{eqn:electric-potential-point-charge-reference} V(\infty) = 0. \end{equation}
Menggunakan Persamaan \eqref{eqn:electric-potential-from-electric-field} dan syarat dari Persamaan \eqref{eqn:electric-potential-point-charge-reference} pada medan listrik akibat muatan titik dari Persamaan \eqref{eqn:electric-field-point-charge-simple} akan memberikan
\begin{equation}\label{eqn:electric-potential-ref-infty} \begin{array}{rcl} V(r) - V(\infty) & = & \displaystyle - \int_\infty^r \vec{E} \cdot d\vec{r} \newline & = & \displaystyle - \int_\infty^r \left( k \frac{q}{r^2} \ \hat{r} \right) \cdot (\hat{r} dr) \newline & = & \displaystyle - \int_\infty^r k \frac{q}{r^2} ( \hat{r} \cdot \hat{r}) dr \newline & = & \displaystyle -kq \int_\infty^r \frac{dr}{r^2} \newline & = & \displaystyle -kq \left[ -\frac{1}{r} \right]_\infty^r \newline & = & \displaystyle kq \left( \frac{1}{r} - \frac{1}{\infty} \right) \newline & = & \displaystyle k \frac{q}{r} \newline V(r) & = & \displaystyle V(\infty) + k \frac{q}{r} \newline & = & \displaystyle k \frac{q}{r}. \end{array} \end{equation}
Baris terakhir dari Persamaan \eqref{eqn:electric-potential-ref-infty} akan konsisten dengan syaratnya pada Persamaan \eqref{eqn:electric-potential-point-charge-reference} saat digunakan $r = \infty$. Cara ini dapat digunakan untuk memeriksa hasil integral dengan syarat batas.
Penjelasan mengenai potential listrik $V$ sebenarnya, mungkin, lebih jelas lewat konsep energi potential listrik $U$, yang keduanya terkait lewat
\begin{equation}\label{eqn:electric-potential-from-electric-potential-energy} U = q V, \end{equation}
dengan $q$ adalah muatan yang memiliki energi potensial listrik tersebut. Gaya listrik $F$ adalah adalah salah satu gaya konservatif sehingga hubungan
\begin{equation}\label{eqn:electric-force-conservative-force} U = - \int \vec{F} \cdot d\vec{r} \end{equation}
juga berlaku.
Sebagai ringkasan dapat disajikan gambar berikut ini.
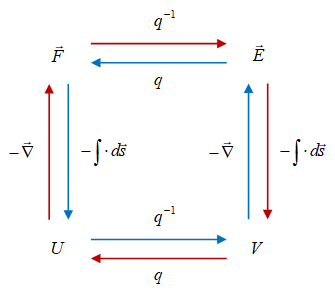
Gambar 2. Hubungan antara gaya listrik $\vec{F}$, medan listrik $\vec{E}$, potensial listrik $V$, dan energi potensial listrik $U$.
Hubungan keempat besaran fisis, gaya listrik $\vec{F}$, medan listrik $\vec{E}$, potensial listrik $V$, dan energi potensial listrik $U$, telah diberikan pada Gambar 2. Untuk saat ini dapat digunakan $\vec{\nabla} = \hat{r}d/dr$ dan $d\vec{s} = d\vec{r}$, yang sebenarnya dapat lebih umum.
Tabel 1. Persamaan yang mengaitkan $\vec{F}$, $\vec{E}$, $V$, dan $U$.
| Gambar 2 | $\color{#07c}{\blacksquare}$ | $\color{#c00}{\blacksquare}$ |
|---|---|---|
| Atas | $\displaystyle \vec{F} = q\vec{E}$ | $\displaystyle \vec{E} = \frac{\vec{F}}{q}$ |
| Kanan | $\vec{E} = -\vec{\nabla}V$ | $\displaystyle V = - \int \vec{E} \cdot d\vec{s}$ |
| Bawah | $\displaystyle V = \frac{U}{q}$ | $U = qV$ |
| Kiri | $\displaystyle U = - \int \vec{F} \cdot d\vec{s}$ | $\vec{F} = -\vec{\nabla}U$ |
Persamaan-persamaan yang terkait dengan hubungan dalam Gambar 2 diberikan dalam Tabel 1.
— Sparisoma Viridi (@6unpnp) January 13, 2022
electrostatic force • electric field • electric potential