spring-mass sign

Hukum Hooke sering diperkenalkan dengan menggunakan sistem yang terdiri sebuah pegas dan benda [1], yang telah terdapat pula simulasinya [2]. Terdaat hal yang menarik mengenai sistem ini, yaitu bahwa tanda pada gaya pegas sering kali masih menjadi pertanyaan [3].

3rd newton’s law

Hukum III Newton secara formal menyatakan [4]

Untuk setiap aksi, terdapat reaksi yang sama besarnya dan arahnya berlawanan.

Pernyataan ini dapat dinyatakan dalam bentuk

\begin{equation}\label{eqn-newton-3rd-law} \vec{F} _{ij} = - \vec{F} _{ji}, \end{equation}

dengan $\vec{F}_{\color{red}{i}\color{blue}{j}}$ merupakan gaya yang bekerja pada benda $\color{red}{i}$ akibat benda $\color{blue}{j}$ dan sebaliknya $\vec{F} _{\color{blue}{j}\color{red}{i}}$ merupakan gaya yang bekerja pada benda $\color{blue}{j}$ akibat benda $\color{red}{i}$. Ingat bahwa untuk Persamaan \eqref{eqn-newton-3rd-law}, gaya aksi dan gaya reaksi, bekerja pada dua benda yang berbeda.

spring-mass system

Suatu sistem pegas-massa dapat diilustrasikan seperti pada gambar berikut ini.

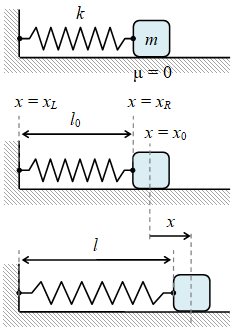
Gambar 1. Sebuah benda bermassa $m$ terikat pada pegas dengan konstanta $k$ dan berada pada suatu lantai mendatar licin dengan $\mu = 0$.

Pegas dengan konstanta pegas $k$ ujung kirinya tertambat pada dinding di sebelah kirinya dan ujung kanannya terikat pada benda bermassa $m$ yang bergerak di atas lantai mendatar licin dengan koefisien gesek antara benda dan lantai $\mu = 0$. Panjang normal pegas adalah $l_0$ dan panjang setiap waktunya adalah $l$ yang dapat lebih besar atau lebih kecil dari $l_0$. Untuk memudahkan koordinat $x = 0$ diambil pada benda saat panjang pegas $l = l_0$ yang sebelumnya merupakan posisi $x = x_0$, atau dengan kata lain dipilih pusat koordinat pada $x = x_0$. Selanjutnya digunakan pula asumsi benda bermassa $m$ merupakan benda titik sehingga posisi kanan pegas $x = x_R$ akan berhimpit dengan posisi benda $x = x_0$ saat panjang pegas $l = l_0$.

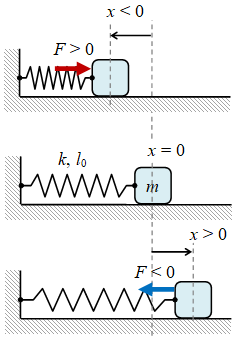
Gambar 2. Gaya pegas yang bekerja pada benda: berarah ke kanan (atas), nol (tengah), dan berarah ke kiri (bawah).

Gaya pada benda oleh pegas umumnya diilustrasikan seperti pada Gambar 2, di mana $F > 0$ saat $x < 0$ dan $F < 0$ saat $x > 0$ sehingga akan memenuhi hubungan

\begin{equation}\label{eqn-spring-force-on-mass} F = -kx, \end{equation}

dengan $x$ adalah simpangan atau posisi benda terhadap titik kesetimbangan. Gaya $F$ adalah gaya yang bersumber dari pegas, atau gaya pegas, yang bekerja pada benda.

force spring

Gaya pegas terkadang dapat menimbulkan dua penafsiran, yaitu gaya pada benda akibat pegas, yang telah dirumuskan dalam Persamaan \eqref{eqn-spring-force-on-mass}, dan gaya pada pegas, yang akan dibahas di sini dengan membedakannya dengan yang pertama.

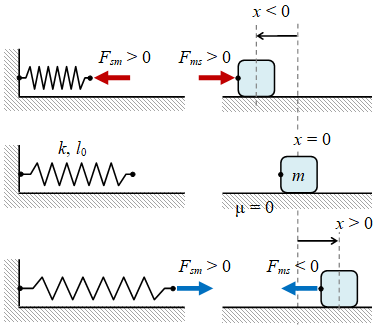
Gambar 3. Perbedaan antara gaya pada pegas karena benda $F_{sm}$ dan gaya pada benda karena pegas $F_{ms}$, dengan indeks $s$ untuk pegas (spring) dan $m$ untuk benda (bermassa $m$).

Dengan menggunakan Persamaan \eqref{eqn-newton-3rd-law} dari hukum III Newton dapat terlihat pada Gambar 3 bahwa pasangan aksi reaksi dalam sistem ini adalah

\begin{equation}\label{eqn-spring-force-action-reaction} \vec{F} _{sm} = \vec{F} _{ms}, \end{equation}

dengan gaya pada benda akibat pegas adalah $\vec{F} _{ms}$ dan gaya pada pegas akibat benda adalah $\vec{F} _{sm}$. Dengan Persamaan \eqref{eqn-spring-force-action-reaction} maka dapat diperoleh

\begin{equation}\label{eqn-spring-force-on-spring} F = kx, \end{equation}

yang merupakan gaya pada pegas, berbeda dengan Persamaan \eqref{eqn-spring-force-on-spring} yang merupakan gaya pada benda. Keduanya sering dituliskan dalam bentuk yang sama dan tertukar.

comparison

Dengan demikian kedua pengertian gaya pegas dapat dibandingkan seperti pada tabel berikut.

Perhatikan pada baris terakhir bahwa tidak ada istilah benda, yang artinya sumber gaya bisa bermacam-macam, seperti benda yang bergerak, benda yang mengalami gaya luar, dan lain-lain. Hal ini berbeda dengan pada baris pertama, di mana sumber gaya pada benda harus berasal dari pegas.

Untuk suatu benda bermassa $m$ yang terikat pada pegas dengan konstanta pegas $k$ dapat berosilasi mengikui persamaan gerak

\begin{equation}\label{eqn-spring-mass-oscillation} \frac{d^2x}{dt^2} + \omega^2 x = 0, \end{equation}

dengan $\omega = \sqrt{k/m}$. Persamaan ini diperoleh dari hukum II Newton dengan gaya luar satu-satunya adalah gaya pegas. Dapatkah Anda memahami apakah Persamaan \eqref{eqn-spring-mass-oscillation} ini merupakan persamaan gerak untuk benda atau untuk pegas?

exer

1. Untuk suatu pegas ideal apa parameter yang menyatakan sifatnya?
2. Apa konsekuensi saat benda $m$, yang terikat pada pegas $k$, dianggap sebagai benda titik?
3. Persamaan \eqref{eqn-spring-mass-oscillation} merupakan persamaan gerak untuk benda atau pegas? Tuliskan formula gaya pegas yang digunakan.
4. Saat melakukan percobaan pembebanan pegas untuk mementukan konstanta pegas, formula gaya pegas mana yang digunakan? Dan bila percobaan hanya dilakukan untuk satu kali pembebanan dengan massa $m$ bagaimana memperoleh nilai $k$?
5. Apa kaitan antara kedua pengertian gaya pegas yang ada?

note

1. “What is Hooke’s Law?”, Khan Academy, url https://www.khanacademy.org/science/physics/work-and-energy/hookes-law/a/what-is-hookes-law [20211127].
2. Denzell Barnett (developer), Matt Pennington (developer), Amy Rouinfar (lead designer), Mike Dubson (original designer), Wendy Adams, Ariel Paul, Kathy Perkins, “Masses and Springs”, PhET, University of Colorado, 2021, url https://phet.colorado.edu/en/simulations/masses-and-springs/credits [20211127].
3. Niklas Järvstråt, “Answer to ‘For a spring, is it F=kx or is it F=-kx?’”, Quora, 25 Sep 2018, url https://qr.ae/pGlIwv [20211127].
4. Tom Henderson, “Newton’s Third Law”, the Physics Classroom, 2021, url https://www.physicsclassroom.com/class/newtlaws/Lesson-4/Newton-s-Third-Law [20211127].

newton’s 3rd law • elasticity • young’s modulus • shear modulus • bulk modulus